, Откуда .

Сила взаимодействия шариков, расположенных на расстоянии друг от друга, определяется по закону Кулона

; .

Выразим в единицах СИ, входящие в формулу величины

; см = 0,1 м; см = м; ;

; Кл; .

Произведём вычисления:

Н.

Задача 2. На двух одинаковых каплях ртути радиусом см находятся одинаковые одноимённые заряды. Определите их модуль, если сила кулоновского отталкивания уравновешивает силу гравитационного притяжения капель. Расстояние между каплями значительно больше их линейных размеров.

Решение.

По условию расстояние между каплями значительно больше их линейных размеров, значит, капли можно считать материальными точками, а заряды на них – точечными зарядами.

Сила кулоновского отталкивания капель определяется законом Кулона

,

где , – заряд одной капли, – расстояние между каплями.

По закону всемирного тяготения определяем силу гравитационного притяжения капель:

,

где – гравитационная постоянная; – масса одной капли;

, – плотность ртути, – объем капли, ;

, откуда ;

.

По условию , т. е.

, отсюда следует

, откуда ;

Кл.

Задача 3. Два одинаковых шарика зарядили так, что заряд одного из них оказался в 5 раз больше другого. Шарики привели в соприкосновение и развели на втрое большее, чем прежде расстояние. Во сколько раз изменилась сила их кулоновского взаимодействия, если их заряды до соприкосновения были разноимённые?

Решение.

Сила взаимодействия шариков определяется по закону Кулона

, где , – заряды шариков; r – расстояние между шариками.

Обозначим заряды шариков до соприкосновения и , а после соприкосновения – и . Пусть , , согласно условию ; так как шарики одинаковые, то

.

Следовательно, до соприкосновения сила взаимодействия будет

, а после соприкосновения

;

(по условию), тогда ;

Находим отношение сил:

, т. е. сила уменьшилась в раз.

Задача 4. Между двумя одноимёнными точечными зарядами  Кл и Кл, расстояние между которыми 9 см, помещают третий заряд так, что все три заряда оказываются в равновесии. Чему равен заряд и каков его знак? На каком расстоянии от первого заряда он находится?

Решение.

По условию задачи все три заряда находятся в равновесии, это означает, что все силы, действующие на каждый заряд со стороны двух других, уравновешены. Согласно первому закону Ньютона равнодействующая этих сил равна нулю. Рассмотрим, какой знак должен иметь заряд , чтобы это условие было выполнено.

Предположим, что .

Рис. 1.2

В данном случае в равновесии может оказаться только заряд , он будет отталкиваться как от заряда , так и от заряда (рис 1.2). Но заряды и уже не смогут оказаться в равновесии, потому что на каждый из них будут действовать по две силы отталкивания, направленные в одну сторону. Суммарное действие этих сил приведёт к тому, что заряды и станут двигаться с ускорением в противоположные стороны от заряда  . Если заряд будет отрицательным, то условие равновесия системы зарядов будет выполнено (рис 1.3).

Рис. 1.3

Действительно, сила притяжения заряда к заряду может оказаться уравновешенной силой отталкивания заряда от заряда . Заряд окажется в равновесии. Точно также сила притяжения заряда к заряду может уравновесить силу отталкивания заряда от заряда ; силы притяжения заряда к зарядам и могут быть уравновешены, если заряд будет расположен ближе к заряду . Таким образом, все три заряда ( и ) будут в равновесии. Но равновесие зарядов будет неустойчивым, так как при любом изменении расстояния между зарядами (уменьшении или увеличении) равновесие нарушится, равнодействующая каждой пары сил будет удалять заряды от равновесия (равновесие называют устойчивым, если при смещении заряда от положения равновесия возникает сила, возвращающая его в это положение).

Для нахождения расстояния между зарядами и воспользуемся условием равновесия заряда : .

По условию заряды точечные, поэтому по закону Кулона

; ,

где ; – расстояние между зарядами и ; – расстояние между зарядами и ;

или .

Так как все величины в полученном уравнении положительные, то можно извлечь корень квадратный из обеих частей уравнения

, отсюда .

Для определения заряда можно воспользоваться равновесием зарядов или .

Согласно условию равновесия заряда :

,

используя закон Кулона, получаем

, отсюда следует:

.

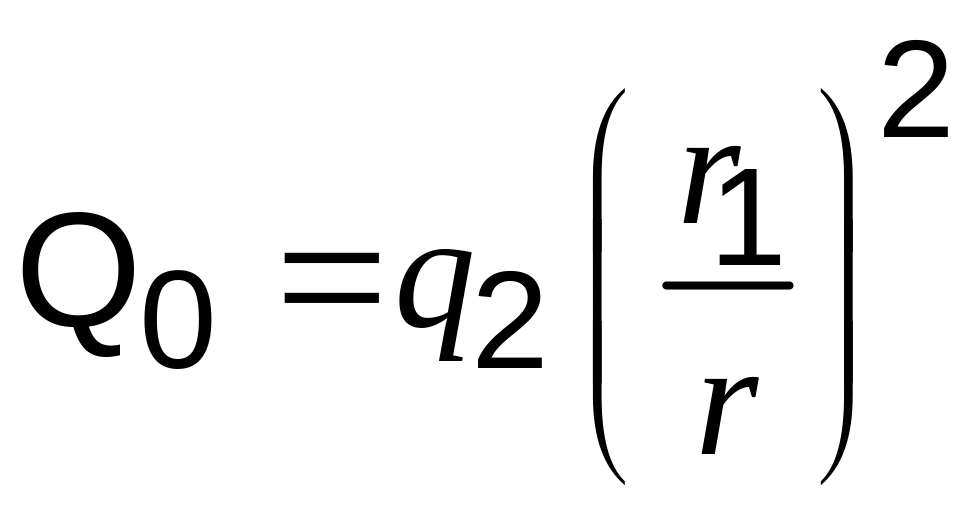Произведём вычисления, переведя все величины в систему СИ:

; .

Кл.

Задача 5. Три одинаковых заряда, каждый из которых равен 2 нКл, расположены в вершинах равностороннего треугольника. Где и какой заряд нужно поместить, чтобы вся система находилась в равновесии?

Решение.

Для равновесия системы зарядов необходимо равновесие каждого заряда системы. Рассмотрим равновесие, например, заряда (рис 1.4).

Н а заряд действуют силы кулоновского отталкивания и со стороны зарядов и .

По закону Кулона ; ,

где (по условию); – коэффициент пропорциональности в системе СИ.

Результирующая сила , действующая на заряд со стороны зарядов и , .

Модуль этой силы находим по теореме косинусов

,

где ; учитывая, что и , получим .

Искомый заряд должен создать силу , действующую на заряд , компенсирующую силу , т. е. .

Заряд не должен находиться на биссектрисе угла .

, где – расстояние от вершины А до заряда .

Следовательно, , откуда .

Заряд должен быть отрицательным по знаку, он будет притягивать к себе каждый из зарядов системы. В силу симметрии расположения зарядов и равенства их модулей для равновесия всей системы необходимо, чтобы заряд был расположен в центре правильного треугольника, т.е. на пересечении биссектрис его внутренних углов (т.0).

Найдём расстояние ,

, тогда ;

и .

Задача 6. Две частицы, имеющие массу и заряд , находятся в вершинах равностороннего треугольника, составленного из лёгких нитей длиной (рис 1.5). Систему поднимают вертикально вверх с ускорением а, равным по модулю . Определите натяжение нити, соединяющей частицы.

Решение.

Рассмотрим ускоренное движение одного из зарядов, например, правого по рис 1.5. На этот заряд действуют следующие силы (рис. 1.6): – сила натяжения нити, связывающей заряд с точкой подвеса (т.В); – сила натяжения нити, связывающей оба заряда; – сила тяжести; – сила кулоновского отталкивания со стороны второго заряда.

Рис. 1.5 Рис. 1.6

Согласно второму закону Ньютона заряд движется при условии:

,

где – равнодействующая всех сил, действующих на заряд .

,

запишем это уравнение в проекциях на оси координат:

,

,

откуда .

Согласно закону Кулона , по условию и (треугольник равносторонний), следовательно,

, .

Задача 7. Полубесконечная нить равномерно заряжена с линейной плотностью заряда . Определить силу, действующую на точечный заряд , расположенный в точке , лежащей против конца нити на расстоянии от неё (рис. 1.7).

Решение:

В данной задаче нельзя определить силу, действующую на заряд со стороны заряженной нити непосредственно по закону Кулона.

Этот закон справедлив лишь для точечных зарядов, а заряд на нити нельзя считать точечным. Чтобы применить закон Кулона, рассмотрим бесконечно малый элемент нити , находящийся на расстоянии от точки (рис. 1.7).

Элемент несёт заряд .

По закону Кулона на заряд будет действовать сила со стороны заряда .

.

Чтобы найти результирующую силу в точке , нужно сложить силы от всех элементов нити, учитывая, что все слагаемые векторы имеют различные направления.

Выберем оси и как показано на рис. 1.7. Найдём проекции вектора на оси координат:

;

.

Проинтегрировав данные выражения по всей длине нити, получим проекции искомого вектора силы в точке и его модуль. В качестве переменной величины, по которой будем проводить интегрирование, удобно выбрать угол , который составляет радиус – вектор с нормалью к нити. Из рис. 1.7. следует

, , тогда

;

.

Угол изменяется от до ;

;

;

.

Задачи для самостоятельного решения

1.1. Два одинаковых иона в воздухе на расстоянии 10^–8 м взаимодействуют с силой Н. Найти число нескомпенсированных электронов у каждого иона.

1.2. С какой силой взаимодействовали бы в воздухе две капли воды массами по 1 г каждая, расположенные на расстоянии 1 м друг от друга, если бы одной из них передали 5 % всех электронов, содержащихся в другой капле?

1.3. Две одинаковые круглые пластины площадью 400 см² каждая расположены параллельно друг другу. Заряд одной пластины 200 нКл, другой –200 нКл. Определить силу взаимного притяжения пластин, если расстояние между ними: а) 3 мм; б) 10 м.

1.4. Два маленьких заряженных шарика взаимодействуют в воздухе с некоторой силой, находясь на расстоянии друг от друга. На каком расстоянии друг от друга они будут взаимодействовать в среде с диэлектрической проницаемостью , если сила их взаимодействия останется прежней?

1.5. Точечные заряды 20 мкКл и –20 мкКл находятся на расстоянии 5 см друг от друга. Определите силу, действующую на заряд 1 мкКл, находящийся в точке, удаленной на 3 см от положительного и на 4 см от отрицательного заряда.

1.6. Три одинаковых точечных заряда 2 нКл находятся в вершинах равностороннего треугольника со стороной 10 см. Определить модуль и направление силы, действующей на один из зарядов со стороны двух других.

1.7. На шелковых нитях, образующих угол , подвешен заряженный шарик массой 10^–3 кг. Снизу к нему подносят шарик с таким же зарядом, в результате чего натяжение нити уменьшается вдвое. Расстояние между шариками 1 см. Определите заряд шариков и натяжение нити в обоих случаях.

1.8. Два одинаковых проводящих шарика подвешены на нитях одинаковой длины см, закреплённых в одной точке. После сообщения шарикам заряда нКл нити разошлись на угол . Определите силу тяжести, действующую на каждый шарик. Какова плотность материала шариков, если при погружении шариков в масло угол расхождения нитей стал 50°?

1.9. Два шарика, каждый массой 0,01 г, подвешены на нитях длиной по 50 см. После того, как шарики были одинаково наэлектризованы, они отошли друг от друга на расстояние 7 см. Найти величину заряда каждого шарика.

1.10. Двух шарикам, массой по 1 г каждый, сообщили отрицательный заряд. Шарики подвешены на нитях длиной по 10 см. После сообщения им заряда нити разошлись на угол 60^о. Сколько электронов сообщили каждому шарику?

1.11. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружают в керосин. Какова плотность керосина, если угол расхождения нитей при погружении шариков в керосин остается неизменным? Плотность материала шариков .

1.12. Два шарика одинакового радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд нужно сообщить шарикам, чтобы сила натяжения нитей стала равной мН. Расстояние от центра шарика до точки подвеса см; масса каждого шарика г.

1.13. Два неподвижных положительных заряда по Кл каждый расположены на расстоянии 0,2 nm друг от друга. Вдоль перпендикуляра, проходящего через середину отрезка, соединяющего эти заряды, движется электрон. В какой точке этого перпендикуляра сила взаимодействия электрона и системы неподвижных зарядов максимальна?

1.14. Четыре маленьких шарика соединены тонкими непроводящими нитями, так что в натянутом состоянии нити образуют ромб. Чему равен угол между нитями если шарики находятся в противоположных вершинах ромба, имеют заряды и ?

1.15. Четыре положительных заряда по 100 нКл каждый помещены в вершинах квадрата. Какой отрицательный заряд надо поместить в центр квадрата, чтобы вся система находилась в равновесии? Будет ли это равновесие устойчивым?

1.16. В вершинах правильного шестиугольника со стороной расположены точечные заряды , , , , , и . C какой силой эти заряды вместе действуют на одноимённый заряд , расположенный в точке пересечения диагоналей шестиугольника?

1.17. Два положительных точечных заряда и закреплены на расстоянии 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.

1.18. Вокруг неподвижного точечного заряда 2 нКл равномерно движется в горизонтальной плоскости, по орбите радиусом см, маленький, отрицательно заряженный шарик. С какой угловой скоростью движется шарик, если удельный заряд этого шарика равен . Среда – воздух.

1.19. По теории Бора электрон вращается вокруг ядра по круговой орбите радиусом м в атоме водорода. Определите скорость вращения электрона.

1.20. Четыре электрона, расположенных в вершинах квадрата со стороной , равномерно вращаются вокруг ядра с зарядом , расположенного в точке пересечения диагонали квадрата. Определить частоту вращения электронов .

1.21. Тонкий стержень длиной 30 см заряжен равномерно с линейной плотностью заряда 2 мкКл/м. На расстоянии 10 см находится заряд 20 нКл, равноудалённый от концов стержня. Найти силу взаимодействия точечного заряда с заряженным стержнем.

1.22. Тонкое кольцо радиуса см несёт равномерно распределённый заряд . На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд нКл. Найти силу на точечный заряд со стороны заряженного кольца, если он удалён от центра кольца на: 1) см, 2) м.

1.23. Точечный заряд находится в поле, созданном прямым бесконечным цилиндром радиуса 1 см с поверхностной плотностью заряда , на расстоянии 20 см от оси цилиндра. Найти силу, действующую на заряд 20 нКл.

1.24. Тонкий очень длинный стержень равномерно заряжен с линейной плотностью заряда, равной 10 мкКл/м. Какова сила , действующая на точечный заряд 10 нКл, находящийся на расстоянии 20 см от стержня, вблизи его середины?

1.25. Тонкая бесконечная нить согнута под углом . Нить несет заряд, равномерно распределенный с линейной плотностью 1 мкКл/м. Определите силу , действующую на точечный заряд 0,1 мкКл, расположенный на продолжении одной из сторон и удаленный от вершины угла на 50 см.

1.26. Тонкое полукольцо радиусом 10 см несет равномерно распределенный заряд с линейной плотностью 1 мкКл/м. В центре кривизны полукольца находится заряд 20 нКл. Определить силу взаимодействия точечного заряда и заряженного полукольца.

1.27. По тонкому кольцу радиусом 10 см равномерно распределен заряд с линейной плотностью 1 мкКл/м. В центре кольца находится заряд 0,4 мкКл. Определить силу , растягивающую кольцо. Взаимодействием зарядов кольца пренебречь.

1.28. С какой силой взаимодействуют длинная проволока с линейной плотностью заряда Кл/м и точечный заряд Кл, находящийся на расстоянии 3 см от проволоки, близко к ее середине?

1.29. Чему равна сила, с которой равномерно заряженное кольцо с линейной плотностью заряда действует на положительно заряженный ион, попавший в центр кольца?

1.30. Прямая бесконечная тонкая нить несет равномерно распределенный по длине заряд 1 мкКл/м. Определить силу, действующую на тонкий стержень длиной , находящийся в плоскости, содержащей нить, перпендикулярно к нити. Ближайший к нити конец стержня находится на расстоянии от нее. Стержень заряжен равномерно с линейной плотностью заряда 0,1 мкКл/м.