- •Жиындар және оларға амалдар қолдану. Нақты сандар жиыны
- •2.Анықтауыштар және олардың қасиеттері. Анықтауыштарды есептеу. Мионер және алгебралық толықтауыш.
- •3)Матрица және оларға қолданылатын амалдар. Кері матрица.
- •4)Сызықты теңдеулер жүйесі. Крамер ережесі.
- •5.Сызықты теңдеулерді шешу Гаусс әдісі
- •6. Жазықтықтағы сызық теңдеуі. Түзудің әртүрлі теңдеулері, бұрыштың коэффициеттік теңдеуі.
- •7)Түзудің нормалдық теңдеуі. Нүктеден түзуге дейінгі қашықтық.
- •8.Екінші ретті сызықтар: шеңбер, эллипс, гипербола, парабола
- •9. Жазықтықтың жалпы теңдеуі және оны зерттеу.
- •10. Кеңістіктегі түзу және оның әртүрлі теңдеулері.
- •11.Анықталмаған интеграл және оның қасиеттері. Интегралдар кестесі.
- •12. Анықталмаған интегралды табу әдістері: тікелей интегралдау, айнымалдарды алмастыру әдісі.
- •13. Анықталмаған интегралды табу: бөліктеп интегралдау әдісі.
- •14. Рационал бөлшектерді интегралдау.
- •15. Анықталған интеграл және оның қасиеттері. Ньютон-Лейбинц формуласы
- •16) Бірінші және екінші текті меншіксіз интегралдар.
- •17) Функ-ның нүктедегі шегі. Бір жақты шектер. Функ-ның шектері туралы теорема.
- •18) Ақырсыз кішкене және ақырсыз үлкен шамалар. Ақырсыз шамаларды салыстыру.
- •19) Үзіліссіз функцияның негізгі қасиеттері.
- •20) Туынды ұғымы. Туындының геометриялық және механикалық мағыналары. Туынды табудың негізгі ережелері. Қарапайым функ-дың туындылары. Қосындыны, көбейтіндіні, бөліндіні дифференциалдау ережелері.
- •21) Функцияның дифференциалы. Дифференциалдың жуықтап есептеулерде қолданылуы.
- •22) Күрделі функция және оның туындысы. Кері функция және оның туындысы. Логарифмдік туынды
- •23) Жоғарғы ретті туындылар мен жоғарғы ретті дифференциалдар. 2-ретті туындының физикалық мағынасы.
- •24) Анықталмағандықтарды Лопиталь ережесі арқылы шешу.
- •25) Функцияның өсуі мен кемуі. Функцияның локалдық экстремумы. Функцияның экстремумының қажетті шарты.
- •26) Функцияның экстремумының жеткілікті шарттары. Қисықтың ойыстығы мен дөңестігінің иілу нүктелері. Қисықтың асимптоталары.
- •27) Екі айнымалды тәуелді функция және оның анықталу облысы, графигі.
- •28) Екі айнымалды функ-ның шегі.
- •29) Дербес туынды. Екінші ретті дербес туындылар. Бағыт бойынша туынды. Градиент
- •30) Екі айнымалды функ-ның экстремумы. Экстремумының қажетті шарттары.
- •32)Ықтималдықтың классикалық анықтамасы
13. Анықталмаған интегралды табу: бөліктеп интегралдау әдісі.
Бөліктеп
интегралдау әдісі. Айталық,
,![]() -дифференциалданатын функциялар болсын.
Онда
-дифференциалданатын функциялар болсын.
Онда
![]() теңдігі орындалады. Немесе
теңдігі орындалады. Немесе
![]() .
Осы теңдіктің екі жағынан интеграл
алайық, сонда
.
Осы теңдіктің екі жағынан интеграл
алайық, сонда
![]() .
Осыдан
.
Осыдан
![]()
![]()
формуласын аламыз. формуласын бөліктеп интегралдау формуласы дейді. Кейбір жағдайда бөліктеп интегралдау формуласын қолдану арқылы берілген интегралды алғашқыға қарағанда анағұрлым жеңіл алынатын интегралға келтіруге болады
1-
мысал.
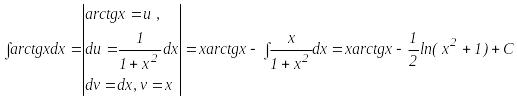
2
- мысал.
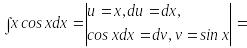
![]() .
.
14. Рационал бөлшектерді интегралдау.
Рационал
бөлшекті интегралдау деп,
![]() интегралын табуды айтады. Мұндағы
интегралын табуды айтады. Мұндағы
![]() дұрыс
рационал бөлшек, яғни
дұрыс
рационал бөлшек, яғни
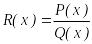
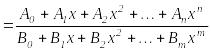 . Егер
. Егер
![]() болса,
дұрыс
бөлшек деп, ал
болса,
дұрыс
бөлшек деп, ал
![]() болса бұрыс бөлшек деп аталады. Бұрыс
бөлшекті интегралдау үшін алдымен
алымын бөліміне бөлу арқылы оны көпмүшелік
пен дұрыс бөлшектің қосындысына
жіктейміз. Мысалы,
болса бұрыс бөлшек деп аталады. Бұрыс
бөлшекті интегралдау үшін алдымен
алымын бөліміне бөлу арқылы оны көпмүшелік
пен дұрыс бөлшектің қосындысына
жіктейміз. Мысалы,
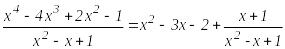
Теорема. Әрбір дұрыс рационал бөлшекті мына қарапайым бөлшектердің қосындысы түрінде жазуға болады:
1.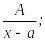 2.
2.
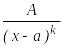
![]() 3.
3.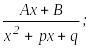 4.
4.
![]() ,
мұндағы А,
В
-
нақты
коэффициенттер;
,
мұндағы А,
В
-
нақты
коэффициенттер;
![]() үшмүшелігінің нақты түбірлері жоқ (яғни
үшмүшелігінің нақты түбірлері жоқ (яғни
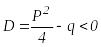 ).
).
Қарапайым бөлшектерді интегралдауды қарастырайық.
![]()
![]() .
.
![]()
![]()
![]() мәнінде
мәнінде
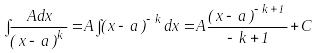 .
.
![]()
 интегралдау
әдісі жоғарыда қарастырылған.
интегралдау
әдісі жоғарыда қарастырылған.
![]() .
.
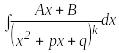 ,
мұндағы
,
мұндағы
![]() және бөліміндегі квадрат үшмүшеліктің
дискриминанты
және бөліміндегі квадрат үшмүшеліктің
дискриминанты
![]() .
Квадрат үшмүшеліктен толық квадрат
бөліп алып
.
Квадрат үшмүшеліктен толық квадрат
бөліп алып
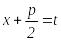 ,
,
![]() ,
алмастыруын жасаймыз. Сонда
,
алмастыруын жасаймыз. Сонда
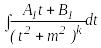 интегралын аламыз және оны екі
интегралдардың қосындысы түрінде
жазамыз. Бірінші интерал
интегралын аламыз және оны екі
интегралдардың қосындысы түрінде
жазамыз. Бірінші интерал
![]() -ны
дифференциал астына енгізу арқылы
интегралданады:
-ны
дифференциал астына енгізу арқылы
интегралданады:
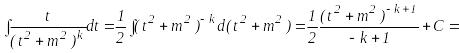
![]() .
.
Ал
екінші интегралды
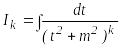 деп белгілеп, төменгідей есептейміз:
деп белгілеп, төменгідей есептейміз:
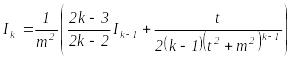
Бұл
формуланы реккуренттік
формула
деп атайды. Реккуренттік формула арқылы
![]() ні
ні
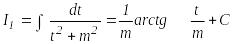 арқылы, ал
арқылы, ал
![]() ті
арқылы
таба отырып, ең соңында
ті
арқылы
таба отырып, ең соңында
![]() ны
ны
![]() арқылы табамыз.
арқылы табамыз.
2-
мысал.
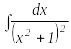 табу керек.
табу керек.
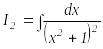 осыдан
осыдан
![]() .
.
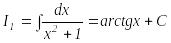 ,
,
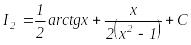 .
Сонымен
.
Сонымен
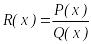 бөлшегінде
болсын. Әрбір
бөлшегінде
болсын. Әрбір
![]() көпмүшелігін
бірінші және екінші дәрежелі
көпмүшеліктердің көбейтіндісіне жіктеп
жазуға болады:
көпмүшелігін
бірінші және екінші дәрежелі
көпмүшеліктердің көбейтіндісіне жіктеп
жазуға болады:
![]() ,
,
мұндағы
![]() бүтін
сандар. Сонда дұрыс бөлшек элементар
бөлшектерге төменгідей жіктелінеді :
бүтін
сандар. Сонда дұрыс бөлшек элементар
бөлшектерге төменгідей жіктелінеді :
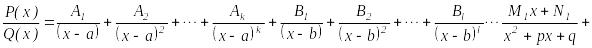
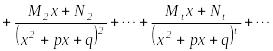
![]()
мұндағы
![]() нақты
сандар. Осы сандарды табу үшін
теңдігінің оң жағын ортақ бөлімге
келтіреміз. Содан соң теңдіктегі екі
бөлшектің бөлімін алып тастасақ, екі
жағында да көпмүшелік шығады. Осы
теңдіктен бірдей дәрежелі
нақты
сандар. Осы сандарды табу үшін
теңдігінің оң жағын ортақ бөлімге
келтіреміз. Содан соң теңдіктегі екі
бөлшектің бөлімін алып тастасақ, екі
жағында да көпмүшелік шығады. Осы
теңдіктен бірдей дәрежелі
![]() тің
алдындағы коэффиценттерді теңестіре
отырып, алгебралық теңдеулер жүйесін
құрамыз. Алынған теңдеулер жүйесінен
тің
алдындағы коэффиценттерді теңестіре
отырып, алгебралық теңдеулер жүйесін
құрамыз. Алынған теңдеулер жүйесінен
![]() коэффиценттерінің мәндерін тауып,
оларды
теңдігіне қоямыз. Осылай рационал
бөлшектің жіктеуін табамыз. Осы әдісті
анықталмаған
коэффициенттер әдісі
дейді.
коэффиценттерінің мәндерін тауып,
оларды
теңдігіне қоямыз. Осылай рационал
бөлшектің жіктеуін табамыз. Осы әдісті
анықталмаған
коэффициенттер әдісі
дейді.
3-мысал.
![]() интегралын есептеу керек. Интеграл
астындағы функция бұрыс рационал бөлшек,
сондықтан алымын бөліміне бөліп дұрыс
бөлшекке айналдырамыз:
интегралын есептеу керек. Интеграл
астындағы функция бұрыс рационал бөлшек,
сондықтан алымын бөліміне бөліп дұрыс
бөлшекке айналдырамыз:
![]() Соңғы қосылғышты қарапайым бөлшектерге
жіктейміз:
Соңғы қосылғышты қарапайым бөлшектерге
жіктейміз:
![]()
Бұдан,
![]()
![]() :
:
![]() ;
;
![]() :
:
![]() ;
;
![]() :
:
![]()
![]() ,
,
![]() ,
,
![]() .
Демек,
.
Демек,
![]() .
Сонымен,
.
Сонымен,