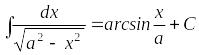- •Жиындар және оларға амалдар қолдану. Нақты сандар жиыны
- •2.Анықтауыштар және олардың қасиеттері. Анықтауыштарды есептеу. Мионер және алгебралық толықтауыш.
- •3)Матрица және оларға қолданылатын амалдар. Кері матрица.
- •4)Сызықты теңдеулер жүйесі. Крамер ережесі.
- •5.Сызықты теңдеулерді шешу Гаусс әдісі
- •6. Жазықтықтағы сызық теңдеуі. Түзудің әртүрлі теңдеулері, бұрыштың коэффициеттік теңдеуі.
- •7)Түзудің нормалдық теңдеуі. Нүктеден түзуге дейінгі қашықтық.
- •8.Екінші ретті сызықтар: шеңбер, эллипс, гипербола, парабола
- •9. Жазықтықтың жалпы теңдеуі және оны зерттеу.
- •10. Кеңістіктегі түзу және оның әртүрлі теңдеулері.
- •11.Анықталмаған интеграл және оның қасиеттері. Интегралдар кестесі.
- •12. Анықталмаған интегралды табу әдістері: тікелей интегралдау, айнымалдарды алмастыру әдісі.
- •13. Анықталмаған интегралды табу: бөліктеп интегралдау әдісі.
- •14. Рационал бөлшектерді интегралдау.
- •15. Анықталған интеграл және оның қасиеттері. Ньютон-Лейбинц формуласы
- •16) Бірінші және екінші текті меншіксіз интегралдар.
- •17) Функ-ның нүктедегі шегі. Бір жақты шектер. Функ-ның шектері туралы теорема.
- •18) Ақырсыз кішкене және ақырсыз үлкен шамалар. Ақырсыз шамаларды салыстыру.
- •19) Үзіліссіз функцияның негізгі қасиеттері.
- •20) Туынды ұғымы. Туындының геометриялық және механикалық мағыналары. Туынды табудың негізгі ережелері. Қарапайым функ-дың туындылары. Қосындыны, көбейтіндіні, бөліндіні дифференциалдау ережелері.
- •21) Функцияның дифференциалы. Дифференциалдың жуықтап есептеулерде қолданылуы.
- •22) Күрделі функция және оның туындысы. Кері функция және оның туындысы. Логарифмдік туынды
- •23) Жоғарғы ретті туындылар мен жоғарғы ретті дифференциалдар. 2-ретті туындының физикалық мағынасы.
- •24) Анықталмағандықтарды Лопиталь ережесі арқылы шешу.
- •25) Функцияның өсуі мен кемуі. Функцияның локалдық экстремумы. Функцияның экстремумының қажетті шарты.
- •26) Функцияның экстремумының жеткілікті шарттары. Қисықтың ойыстығы мен дөңестігінің иілу нүктелері. Қисықтың асимптоталары.
- •27) Екі айнымалды тәуелді функция және оның анықталу облысы, графигі.
- •28) Екі айнымалды функ-ның шегі.
- •29) Дербес туынды. Екінші ретті дербес туындылар. Бағыт бойынша туынды. Градиент
- •30) Екі айнымалды функ-ның экстремумы. Экстремумының қажетті шарттары.
- •32)Ықтималдықтың классикалық анықтамасы
11.Анықталмаған интеграл және оның қасиеттері. Интегралдар кестесі.
Анықтама.
Егер
![]() аралығында берілген
аралығында берілген
![]() функциясы үшін
функциясы үшін
![]() теңдігі
орындалса, онда
теңдігі
орындалса, онда
![]() функциясы
функциясының
функциясы
функциясының
![]() аралығындағы
алғашқы
функциясы
деп аталады. Басқаша айтқанда, берілген
функцияның алғашқы функциясын табу –
оның туындысын табуға кері есеп болып
саналады.
аралығындағы
алғашқы
функциясы
деп аталады. Басқаша айтқанда, берілген
функцияның алғашқы функциясын табу –
оның туындысын табуға кері есеп болып
саналады.
![]() кез
келген тұрақты шама (константа), яғни
кез келген сан болсын. Егер
функциясының алғашқы функциясы
болса, онда
кез
келген тұрақты шама (константа), яғни
кез келген сан болсын. Егер
функциясының алғашқы функциясы
болса, онда
![]() функциясы да оның алғашқы функциясы
болады, себебі
функциясы да оның алғашқы функциясы
болады, себебі
![]() .
функциясы
функциясының барлық алғашқы функцияларын
анықтайды.
.
функциясы
функциясының барлық алғашқы функцияларын
анықтайды.
Анықтама.
Егер
болса, онда
функциясын
функциясының анықталмаған интегралы
дейді және ол
![]() символымен белгіленеді.
символымен белгіленеді.
Сонымен,
![]() мұндағы
мұндағы
![]() интеграл
белгісі,
интеграл
белгісі,
![]() -
-
![]() айнымалысының дифференциалы,
айнымалысының дифференциалы,
![]() -интеграл астындағы өрнек. Берілген
функцияның анықталмаған интегралын
табу жолын осы функцияны интегралдау
дейді.
-интеграл астындағы өрнек. Берілген
функцияның анықталмаған интегралын
табу жолын осы функцияны интегралдау
дейді.
Анықталмаған интегралдардың қасиеттері
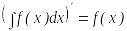
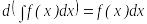
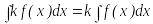 ,
мүндағы
,
мүндағы
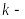 кез
келген сан.
кез
келген сан.
4.
![]()
5.
![]() ,
мұндағы
,
мұндағы
![]() -
кез келген сан.
-
кез келген сан.
Анықталмаған интегралдардың негізгі кестесі
1.
2.
3.
Дербес
жағдайда,
4.
5.
6.
7.
8.
9. |
11.
12.
13.
14. .
15.
16.
17.
18.
19.
|
12. Анықталмаған интегралды табу әдістері: тікелей интегралдау, айнымалдарды алмастыру әдісі.
1. Анықталмаған интегралда айнымалыларды алмастыру. Айнымалыны алмастыру әдісі мына формулаға негізделген
![]()
![]()
Мұндағы
![]() - берілген аралықта дифференциалданатын
функция. Тиімді табылған айнымалыны
алмастыру формуласы берілген интегралды
жеңіл интегралдайтын интегралға, ал
кейбір жағдайларда таблицалық интегралға
келтіреді.
- берілген аралықта дифференциалданатын
функция. Тиімді табылған айнымалыны
алмастыру формуласы берілген интегралды
жеңіл интегралдайтын интегралға, ал
кейбір жағдайларда таблицалық интегралға
келтіреді.
1-
мысал.
![]() интегралын табу керек.
интегралын табу керек.
Ол
үшін
![]() алмастыруын жасаймыз. Сонда
алмастыруын жасаймыз. Сонда
![]() болады.
болады.
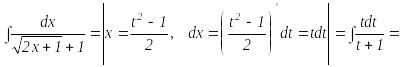
=![]()
![]() .
.
Мұнда интегралдаудың соңында бастапқы - айнымалысына көшу керек.
2.
Дифференциал астына енгізу әдісі. Бұл
әдіс айнымалыны ауыстыру сияқты жиі
қолданылады. Интеграл астындағы
функцияның көбейткіштерінің біреуін
![]() белгісінің астына жазамыз да, оны жаңа
айнымалы ретінде қарастырамыз. Еске
сала кетейік,
белгісінің астына жазамыз да, оны жаңа
айнымалы ретінде қарастырамыз. Еске
сала кетейік,
![]() функциясын
таңбасының астына жазғанда
таңбасынан кейін функцияның алғашқы
функциясы жазылады, яғни
функциясын
таңбасының астына жазғанда
таңбасынан кейін функцияның алғашқы
функциясы жазылады, яғни
![]() .
.
Салдар.
Айталық
![]() үзіліссіз және
үзіліссіз және
![]() үзіліссіз дифференциалданатын функциялар
болсын, онда
үзіліссіз дифференциалданатын функциялар
болсын, онда
![]()
![]()
2-мысал.![]() .
Бұл формулада
таңбасының астына
.
Бұл формулада
таңбасының астына
![]() функциясын енгізіп
функциясын енгізіп
![]() деп жаздық. Модуль
таңбасын қолданбаса да болады, себебі
интеграл астындағы функция тек
деп жаздық. Модуль
таңбасын қолданбаса да болады, себебі
интеграл астындағы функция тек
![]() болғанда
анықталады. Дифференциал
таңбасы астында кез келген функцияның
алғашқы функциясына тұрақтыны қосып
пайдалануға болады.
болғанда
анықталады. Дифференциал
таңбасы астында кез келген функцияның
алғашқы функциясына тұрақтыны қосып
пайдалануға болады.
3-
мысал.
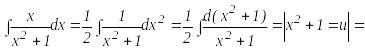
![]() .
.

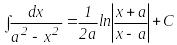 .
.