
- •Жиындар және оларға амалдар қолдану. Нақты сандар жиыны
- •2.Анықтауыштар және олардың қасиеттері. Анықтауыштарды есептеу. Мионер және алгебралық толықтауыш.
- •3)Матрица және оларға қолданылатын амалдар. Кері матрица.
- •4)Сызықты теңдеулер жүйесі. Крамер ережесі.
- •5.Сызықты теңдеулерді шешу Гаусс әдісі
- •6. Жазықтықтағы сызық теңдеуі. Түзудің әртүрлі теңдеулері, бұрыштың коэффициеттік теңдеуі.
- •7)Түзудің нормалдық теңдеуі. Нүктеден түзуге дейінгі қашықтық.
- •8.Екінші ретті сызықтар: шеңбер, эллипс, гипербола, парабола
- •9. Жазықтықтың жалпы теңдеуі және оны зерттеу.
- •10. Кеңістіктегі түзу және оның әртүрлі теңдеулері.
- •11.Анықталмаған интеграл және оның қасиеттері. Интегралдар кестесі.
- •12. Анықталмаған интегралды табу әдістері: тікелей интегралдау, айнымалдарды алмастыру әдісі.
- •13. Анықталмаған интегралды табу: бөліктеп интегралдау әдісі.
- •14. Рационал бөлшектерді интегралдау.
- •15. Анықталған интеграл және оның қасиеттері. Ньютон-Лейбинц формуласы
- •16) Бірінші және екінші текті меншіксіз интегралдар.
- •17) Функ-ның нүктедегі шегі. Бір жақты шектер. Функ-ның шектері туралы теорема.
- •18) Ақырсыз кішкене және ақырсыз үлкен шамалар. Ақырсыз шамаларды салыстыру.
- •19) Үзіліссіз функцияның негізгі қасиеттері.
- •20) Туынды ұғымы. Туындының геометриялық және механикалық мағыналары. Туынды табудың негізгі ережелері. Қарапайым функ-дың туындылары. Қосындыны, көбейтіндіні, бөліндіні дифференциалдау ережелері.
- •21) Функцияның дифференциалы. Дифференциалдың жуықтап есептеулерде қолданылуы.
- •22) Күрделі функция және оның туындысы. Кері функция және оның туындысы. Логарифмдік туынды
- •23) Жоғарғы ретті туындылар мен жоғарғы ретті дифференциалдар. 2-ретті туындының физикалық мағынасы.
- •24) Анықталмағандықтарды Лопиталь ережесі арқылы шешу.
- •25) Функцияның өсуі мен кемуі. Функцияның локалдық экстремумы. Функцияның экстремумының қажетті шарты.
- •26) Функцияның экстремумының жеткілікті шарттары. Қисықтың ойыстығы мен дөңестігінің иілу нүктелері. Қисықтың асимптоталары.
- •27) Екі айнымалды тәуелді функция және оның анықталу облысы, графигі.
- •28) Екі айнымалды функ-ның шегі.
- •29) Дербес туынды. Екінші ретті дербес туындылар. Бағыт бойынша туынды. Градиент
- •30) Екі айнымалды функ-ның экстремумы. Экстремумының қажетті шарттары.
- •32)Ықтималдықтың классикалық анықтамасы
9. Жазықтықтың жалпы теңдеуі және оны зерттеу.
1. Берілген нүкте арқылы, берілген векторға перпендикуляр өтетін жазықтықтың теңдеуі
Жазықтықта
![]() нүктесі
және оған перпендикуляр
нүктесі
және оған перпендикуляр
![]() векторы берілсін. Сонда берілген нүкте
арқылы, берілген векторға перпендикуляр
өтетін жазықтықтың теңдеуі төменгідей
болады:
векторы берілсін. Сонда берілген нүкте
арқылы, берілген векторға перпендикуляр
өтетін жазықтықтың теңдеуі төменгідей
болады:
![]() (5.1)
(5.1)
2. Жазықтықтың жалпы теңдеуі
![]() (5.2)
(5.2)
Егер D=0 болса, онда жазықтық бас нүкте арқылы өтеді ; егер C=0 онда, жазықтық Oz өсіне параллель өтеді; егер C=D=0 болса, онда жазықтық бас нүкте арқылы Oz өсіне параллель өтеді; егер A=B=D=0 болса, онда z=0 болады. Бұл Oxy жазықтығы.
3.
Үш нүкте арқылы өтетін жазықтықтың
теңдеуі.
,
![]() және
және
![]() нүктелері
арқылы өтетін жазықтықтың теңдеуі:
нүктелері
арқылы өтетін жазықтықтың теңдеуі:
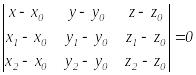 (5.3)
(5.3)
4. Жазықтықтың кесінділік теңдеуі
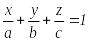 (5.4)
(5.4)
5.
Екі жазықтықтың арасындағы бұрыш.
Жазықтықтар
![]() және
және
![]() теңдеулерімен берілсе, онда
теңдеулерімен берілсе, онда
![]() ,
,
![]() болғандықтан жазықтықтардың арасындағы
бұрыш осы екі нормальдің арасындағы
бұрышқа тең:
болғандықтан жазықтықтардың арасындағы
бұрыш осы екі нормальдің арасындағы
бұрышқа тең:
 (5.5)
(5.5)
Осыдан
егер жазықтықтар параллель болса, онда
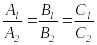 ,
ал перпендикуляр болса, онда
,
ал перпендикуляр болса, онда
![]() болады.
болады.
6. Нүктеден түзуге дейінгі қашықтық
![]() нүктесінен
түзуіне дейінгі қашықтықтың формуласы:
нүктесінен
түзуіне дейінгі қашықтықтың формуласы:
 (5.6)
(5.6)
10. Кеңістіктегі түзу және оның әртүрлі теңдеулері.
Кеңістіктегі түзудің теңдеулері
1.
Екі нүкте арқылы өтетін түзудің теңдеуі.
Түзу
![]() және
және
![]() нүктелерінен өтсе, онда оның теңдеуі:
нүктелерінен өтсе, онда оның теңдеуі:
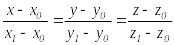 (5.7)
(5.7)
2. Түзудің канондық теңдеуі
нүктесі
түзудің бойында жатсын және ол түзу
![]() векторына параллель болсын. Түзудің
бойынан кез келген
векторына параллель болсын. Түзудің
бойынан кез келген
![]() нүктесін аламыз. Сонда,
нүктесін аламыз. Сонда,
![]() .
.
![]() векторы түзудің бойында жатқандықтан
||
векторы түзудің бойында жатқандықтан
||![]() болады. Сондықтан түзудің канондық
теңдеуі:
болады. Сондықтан түзудің канондық
теңдеуі:
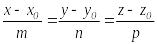 (5.8)
(5.8)
Мұндағы - бағыттаушы вектор деп аталады.
3.
Түзудің параметрлік теңдеуі. (5.7)
теңдеуіндегі әр теңдікті
![]() ға
теңеп, мына теңдеуді аламыз:
ға
теңеп, мына теңдеуді аламыз:
![]() (5.9)
(5.9)
4. Түзудің жалпы теңдеуі. Өзара параллель емес екі жазықтық жалпы теңдеулерімен берілсін:
, (5.10)
Сонда бұл жазықтықтар бір түзудің бойымен қиылысады. Ендеше осы екі жазықтықтың қиылысқан түзуінің бойындағы кез келген нүктенің координаттары екі жазықтықтың да теңдеуін қанағаттандырады. Сондықтан осы екі теңдеулер жүйесін түзудің жалпы теңдеуі дейді.
5. Екі түзудің арасындағы бұрыш. Екі түзу канондық теңдеулерімен берілсін:
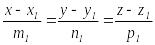 және
және
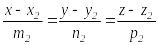 Екі түзудің арасындағы бұрыш, сол
түзулердің бағыттаушы векторларының
арасындағы бұрышқа тең (
Екі түзудің арасындағы бұрыш, сол
түзулердің бағыттаушы векторларының
арасындағы бұрышқа тең (![]() ,
,![]() ):
):
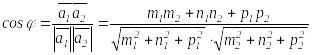 (5.10)
(5.10)
Егер
түзулер өзара параллель болса, онда
![]() ||
||![]() болады.
Түзулердің параллелдік шарты:
болады.
Түзулердің параллелдік шарты:
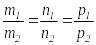 ,
егер түзулер өзара перпендикуляр болса,
онда
,
егер түзулер өзара перпендикуляр болса,
онда
![]() болады. Түзулердің перпендикулярлық
шарты:
болады. Түзулердің перпендикулярлық
шарты:
![]() болады.
болады.
Түзу мен жазықтық. Жалпы теңдеуімен берілген жазықтық пен канондық теңдеуімен түзудің арасындағы бұрышты табу керек.
Түзу мен жазықтықтың арасындағы бұрыш деп, осы түзу мен оның жазықтыққа түсірілген проекциясының арасындағы сыбайлас бұрыштың біреуін айтады. Түзу мен жазықтықтың арасындағы бұрыштың синусы мына формуламен есептелінеді:
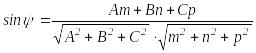 (5.11)
(5.11)
Түзу
мен жазықтықтың параллелдік белгісі:
![]() .
Түзу мен жазықтықтың перпендикулярлық
белгісі:
.
Түзу мен жазықтықтың перпендикулярлық
белгісі:
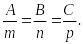
1-мысал.![]() түзуі мен
түзуі мен
![]() жазықтығының арасындағы бұрыштың синусы
мен қиылысу нүктесін табу керек.
жазықтығының арасындағы бұрыштың синусы
мен қиылысу нүктесін табу керек.
![]() ,
ал
,
ал
![]() болғандықтан
болғандықтан
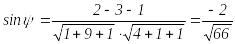 .
Қиылысу нүктесін табу үшін түзу мен
жазықтықтың теңдеулер жүйесін шешеміз.
Сонда
.
Қиылысу нүктесін табу үшін түзу мен
жазықтықтың теңдеулер жүйесін шешеміз.
Сонда
![]()
![]()
![]() .
Осыдан
.
Осыдан
![]() ,
яғни
,
яғни
![]() .
.
