7)Түзудің нормалдық теңдеуі. Нүктеден түзуге дейінгі қашықтық.

және түзулерінің арасындағы бұрыштың формуласы:

Осыдан егер түзулер параллель болса, онда , ал түзулер перпендикуляр болса, онда болады. Түзулер және теңдеулерімен берілсе, онда , болғандықтан түзулердің арасындағы бұрыш осы екі нормальдің арасындағы бұрышқа тең:

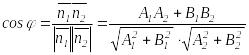(4.8)

Осыдан егер түзулер параллель болса, онда , ал перпендикуляр болса, онда болады.

2-мысал. нұктесінен тұзуіне дейінгі қашықтықты табу керек.

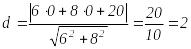
Нүктеден түзуге дейінгі қашықтық.Тік бұрышты координаталар жүйесінде қандай да бір түзу Ах+Вх+С=0 және түзуден тыс жатқан нүкте М(х₀,у₀) берілсін.Нүктеден түзуге дейінгі қашықтық деп нүктеден түзуге түсірілген перпендикуляр ұзындығын айтамыз.Суретте ол d=MN.Осы ара қашықтықты табу үшін:а)берілген түзуге перпендикуляр және М(х₀,у₀) нүктесі арқылы өтетін түзу теңдеуін тауып аламыз;б)берілген түзу мен MN түзулерінің теңдеуін жүйе етіп шешіп,олардың қиылысу нүктесі N(х₁,у₁) табамыз; в)екі нүктенің ара қашықтығын есептейтін формула көмегімен d=MN ара қашықтықты есептейміз.Нәтижесінде мынадай формула алынады:d=

8.Екінші ретті сызықтар: шеңбер, эллипс, гипербола, парабола

1. Шеңбер

Анықтама. Центр деп аталатын берілген нүктеден бірдей қашықтықта жататын жазықтықтағы нүктелердің геометриялық орындарын шеңбер деп атайды.

(6.1)

(6.1) – теңдеуі центрі С нүктесінде жатқан радиусы R-ге тең шеңбердің теңдеуі.

Егер шеңбердің центрі С координаттардың бас нүктесінде жатса, яғни болса, онда (6.1) мына түрге келеді:

(6.2)

Мысалы:A(1;5),B(-4;0)ж/е C(4;-4)нүктелерінен өтетін шеңбердің центрі мен радиусын анықтаңыз ж/е осы шеңбердің теңдуін жазыңыз:Шешуі: теңд-гі a,b ж/еR шамаларын табамыз.А,В ж/е С нүк-і ізделінеді шеңберде жатқандықтан, олардың коорд-ры теңдеуді қанағаттандырады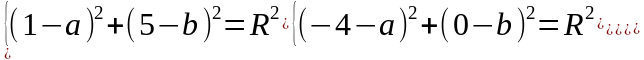

Бұл жүйенің екінші теңдеуінен алдымен бірінші теңдеуді,содан соң үшінші теңдуді айырсақ,келесі жүйеге ие боламыз. 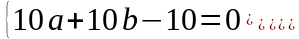осы жүйені шешсек,a=1;b=0 шығады. Бұл табылған мәндерді бастапқы жүйенің біреуіне қойсақ, теңдігі шығады,яғни R=5. Сонымен ізделінді шеңбер теңдеуі болып,оның центрі C(-1;2)нүктесі,ал радиусы R=5.

2. Эллипс

Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды.

Анықтама бойынша , мұндағы және - фокустар деп аталатын берілген нүктелер, -эллипстің бойындағы кез келген нүкте, -тұрақты шама.

Егер десек, онда , . Енді осы мәндерді теңдеуіне қойып, түрлендіріп, эллипстің канондық теңдеуін аламыз:

(6.3)

мұндағы эллипстің үлкен жарты өсі, оның кіші жарты өсі болады. ны табу үшін эллипстің бойынан нүктесін аламыз. болғандықтан немесе болады. Пифагор теоремасы бойынша . Осыдан деп белгілейміз. қатынасын эллипстің эксцентриситеті деп атайды. болғандықтан . эллипстің директрисаларының теңдеуі. Ол эллипстің сыртында жатады.

Канондық теңд: мұндағы -э-ң эксцентриситеті, фокустық радиустар a-үлкен жарты ось, b-кіші жарты ось.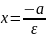 ( ж/е 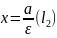түзулер эллипстің директрисалары.b болғанда фокустар Оу осьте жатады ж/е , қатынастар орындалады.

Мысалы .9x²+25y²=225 элипс берілген.Оның жарты осьтерінің ұзындықтарын фокустарын координаталарын эксцентриситеті мен дирексиясын табу керек.

Берілген теңдеуді 225- ке мүшелеп бөлсек теңдеу канондық түрге келеді:X²∕25+Y²∕9=1

Бұдан шығатын a²=25,b²=9 Яғни a=5,b=3 -эллпстің үлкен және кіші осьтер ұзындықтары .b=√a²-c² теңдіктен c=√a²-b² болып, жоғарғыда мәндерді қойсақ, c=√25-9=4 шығады. Демек F(-4;0) және F(4;0) берілген эллипстің фокустары .Ал эксцентриситеті Ɛ=c∕a=4∕5=0,8; директрисалар

X=±5/0,8=±6,25

3. Гипербола

\Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырмасының абсолюттік шамасы тұрақты 2а-ға тең болатын жазықтықтағы нүктелердің геометриялық орындарын гипербола деп атайды.

Гиперболаның канондық теңдеуі былай жазылады:

(6.4)

Мұндағы , - гиперболаның нақты жарты өсі, жорымал жарты өсі, гиперболаның эксцентриситеті, болғандықтан . Егер гиперболаның нүктесі шексіздікке ұмтылғанда нүктесінен түзуге дейінгі қашықтық нөлге ұмтылса, онда мұндай түзуді гиперболаның асиптотасы дейді. Гиперболаның асимптоталарының теңдеулері: және , мұндағы және гиперболаның жарты өстері. гиперболаның директрисаларының теңдеуі. Гиперболаның директрисалары оның төбелерінің арасында жатады.

4. Парабола

Анықтама. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын жазықтықтағы нүктелердің геометриялық орындарын парабола дейді.

(6.5)

мұндағы берілген фокус пен директрисаның арасындағы қашықтық. Параболаның директрисасының теңдеуі: . параболасы өсіне симметриялы орналасады.

5. Екінші ретті қисықтың жалпы теңдеуі

(6.6)

Теорема. (6.6) теңдеуі әрқашан не шеңберді (егер ), не эллипсті (егер ), не гиперболаны (егер ), не параболаны (егер ) анықтайды. Бұл жағдайларда эллипс (шеңбер) нүктеге немесе жорымал эллипске (шеңберге), гипербола қиылысатын түзулердің жұбына, парабола параллель түзулердің жұбына айналуы мүмкін.

1-мысал. теңдеуін канондық түрге келтіру керек.

эллипстің теңдеуі.

. Осыдан деп белгілесек -эллипстің канондық теңдеуі, Бұл жүйенің басы нүктесінде орналасқан.