6. Жазықтықтағы сызық теңдеуі. Түзудің әртүрлі теңдеулері, бұрыштың коэффициеттік теңдеуі.

1)Жазықтықтағы сызық теңдеуі

Берілген Oxy координаталар жүйесінде берілген L сызықтың кез келген нүктесінің координаталары

F(x,y)=0

Теңдеуін қанағаттандырса, ал L сызықта жатпайтын нүктенің координаталар бұл теңдеуі қанағаттандырса, онда теңдеу L сызықтың теңдеуі деп аталады айнымалы координаталар ал әріппен берілген тұрақтыларды параметр деп атайды.

1)Ыңғайлы Oxy координаталар жүйесін таңдап берілген сызықтың кез келген нүктесінM(x,y) деп аталады

2)Барлық M(x,y)нүктелерінің ортақ қасиеті геометриялық теңдік түрінде жазылады.

3)Бұл теңдікке кірген кесінді мен бұрыштарды x,y координаталар және берілген шамалар арқылы алгебралық түрде өрнектеу

Берілген F(x,y)=0 және Ф(x,y)=0 екі сызықтың қиылысу нүктелерін табу үшін олардың теңдеуі жүйе етіп шешіледі.

Мысалы Радиусы R центрі нүктесі C(a,b) болатын шеңбердің теңдеуін жазу керек.

Шешуі :Шеңбердің кез келген M(x,y) нүктесін аламыз және оны C(a,b)центрмен қосамыз. Шеңбердің анықтамасы бойынша M(x,y) нүктелерінің жалпы қасиеті CM=R теңдікпен жазылады. енді екі нүкте арасындағы арақашықтық √(x-a)²+(y-b)²=R бұдан мыны теңдеу шығады

(x-a)²+(y-b)²=R²

2). жазықтықтағы түзудің әр түрлі теңдеулері. Жазықтықтағы түзу (1-сурет) Оу осін В(0;b) нүктесінде қиып, Ох осімен 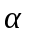(0< < ) бұрыш жасасын. Түзу бойынан қандай да бір М(х,у) нүкте алайық. Түзудің Ох осімен жасаған бұрышының тангенсін ВМК үшбұрышынан табамыз: деп белгілеп, түзудің бұрыштық коэффициенті деп атау қабылданған. Сонымен .Осы қатынастан у-ті тапсақ: y=kx+b Түзу бойында жатқан кез келген нүктенің координатасы (2) теңдеуді қанағаттандырады да түзуден тыс жатқан нүктелер бұл теңдеуді қанағаттандырмайды. (2) теңдеу түзудің бұрыштық коэффициентімен берілген теңдеуі деп аталады. Дербес жағдайларын қарастырайық.

1. Түзудің бұрыштық коэффициентімен берілген теңдеуіндегі b=0 болсын. Онда түзу теңдеуі y=kx түрге келеді де, түзу координат басынан өтеді

2. Егер болса, онда болады да, түзу теңдеуі y=b түрге келеді де, түзу Ох осіне параллель болады (3-сурет). Ал Ох осінің теңдеуі y=0 болады.

3. Егер болса, онда мәні болмайды, түзу Ох осіне перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің теңдеуі х=0 болады.

Мынадай теорема айтуға болады.

Теорема. Тік бұрышты координаталар жүйесінде кез келген түзу бірінші ретті теңдеумен беріледі Ах+Ву+С=0 Және керісінше, (3) теңдеу (А, В, С коэффициенттердің бәрі бір мезгілде нолге тең болмаған кезде) тік бұрышты координаталар жүйесінде қандай да бір түзуді анықтайды. теңдеуді әдетте түзудің жалпы теңдеуі деп атайды.

Берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуі. Көп жағдайда түзу теңдеуін оның бойында жатқан белгілі нүкте мен k бұрыштық коэффициенті арқылы жазу керек болады

Түзу теңдеуін (2) түрінде жазайық, y=kx+b, мұндағы b әзірше белгісіз. Түзу нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₁=kx₁+b. Осы теңдіктен белгісіз b табылады, b = y₁ - kx_1. Табылған мәнді теңдеудегі орнына қойып, берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуін аламыз: y =k(x – x₁)+ y₁ Егер (4) теңдеудегі k ерікті мән қабылдаса, онда теңдеу нүктесі арқылы өтетін түзулер шоғының теңдеуін анықтайды .Берілген екі нүкте арқылы өткен түзу теңдеуі. 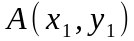және нүктелері берілсін. АВ түзуінің теңдеуін жазу үшін А нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз:

y =k(x – x₁)+ y_1.

АВ түзуі нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₂ =k(x₂ – x₁)+ y_1. Осы теңдіктен белгісіз k табылады, . Табылған мәнді теңдеудегі орнына қойып, берілген екі нүкте арқылы өткен түзу теңдеуін аламыз: .