
- •Жиындар және оларға амалдар қолдану. Нақты сандар жиыны
- •2.Анықтауыштар және олардың қасиеттері. Анықтауыштарды есептеу. Мионер және алгебралық толықтауыш.
- •3)Матрица және оларға қолданылатын амалдар. Кері матрица.
- •4)Сызықты теңдеулер жүйесі. Крамер ережесі.
- •5.Сызықты теңдеулерді шешу Гаусс әдісі
- •6. Жазықтықтағы сызық теңдеуі. Түзудің әртүрлі теңдеулері, бұрыштың коэффициеттік теңдеуі.
- •7)Түзудің нормалдық теңдеуі. Нүктеден түзуге дейінгі қашықтық.
- •8.Екінші ретті сызықтар: шеңбер, эллипс, гипербола, парабола
- •9. Жазықтықтың жалпы теңдеуі және оны зерттеу.
- •10. Кеңістіктегі түзу және оның әртүрлі теңдеулері.
- •11.Анықталмаған интеграл және оның қасиеттері. Интегралдар кестесі.
- •12. Анықталмаған интегралды табу әдістері: тікелей интегралдау, айнымалдарды алмастыру әдісі.
- •13. Анықталмаған интегралды табу: бөліктеп интегралдау әдісі.
- •14. Рационал бөлшектерді интегралдау.
- •15. Анықталған интеграл және оның қасиеттері. Ньютон-Лейбинц формуласы
- •16) Бірінші және екінші текті меншіксіз интегралдар.
- •17) Функ-ның нүктедегі шегі. Бір жақты шектер. Функ-ның шектері туралы теорема.
- •18) Ақырсыз кішкене және ақырсыз үлкен шамалар. Ақырсыз шамаларды салыстыру.
- •19) Үзіліссіз функцияның негізгі қасиеттері.
- •20) Туынды ұғымы. Туындының геометриялық және механикалық мағыналары. Туынды табудың негізгі ережелері. Қарапайым функ-дың туындылары. Қосындыны, көбейтіндіні, бөліндіні дифференциалдау ережелері.
- •21) Функцияның дифференциалы. Дифференциалдың жуықтап есептеулерде қолданылуы.
- •22) Күрделі функция және оның туындысы. Кері функция және оның туындысы. Логарифмдік туынды
- •23) Жоғарғы ретті туындылар мен жоғарғы ретті дифференциалдар. 2-ретті туындының физикалық мағынасы.
- •24) Анықталмағандықтарды Лопиталь ережесі арқылы шешу.
- •25) Функцияның өсуі мен кемуі. Функцияның локалдық экстремумы. Функцияның экстремумының қажетті шарты.
- •26) Функцияның экстремумының жеткілікті шарттары. Қисықтың ойыстығы мен дөңестігінің иілу нүктелері. Қисықтың асимптоталары.
- •27) Екі айнымалды тәуелді функция және оның анықталу облысы, графигі.
- •28) Екі айнымалды функ-ның шегі.
- •29) Дербес туынды. Екінші ретті дербес туындылар. Бағыт бойынша туынды. Градиент
- •30) Екі айнымалды функ-ның экстремумы. Экстремумының қажетті шарттары.
- •32)Ықтималдықтың классикалық анықтамасы
4)Сызықты теңдеулер жүйесі. Крамер ережесі.
n белгісізі бар m сызықтық теңдеулер жүйесі

түрінде
беріледі, мұндағы
 -белгісіз
шамалар, ал
-белгісіз
шамалар, ал
 -сандар,
жүйенің коэффиценттері,
-сандар,
жүйенің коэффиценттері,
 -бос
мүшелер –
берілген сандар.
-бос
мүшелер –
берілген сандар.
Кронеккер-Капелли теоремасы. Егер сызықты теңдеулер жүйесінің негізгі матрицасы мен кеңейтілген матрицасының ранглері тең болса, онда жүйе үйлесімді болады.
Теорема
бойынша жүйе үйлесімді болуы үшін
 болуы керек. Бұл кезде r
жүйе
рангісі
деп аталады.
болуы керек. Бұл кезде r
жүйе
рангісі
деп аталады.
Крамер әдісімен шешу. Бұл әдіс жүйедегі теңдеулер саны мен белгісіздер саны тең болғанда, яғни m=n, қолдануға болады. Демек, жүйе түрі мынадай болады:
 (4)
(4)
Жүйедегі
теңдеулер саны мен белгісіздер саны
тең, онда жүйе матрицасы квадрат матрица
болады. Сол квадрат матрицаның анықтауышын
 деп белгілейік:
деп белгілейік:

Крамер
ережесі.
-жүйе
анықтауышы, ал
 -
анықтауыштың j-тік жолын бос мүшелермен
алмастырғаннан пайда болған анықтауыш
болсын. Сонда, егер
-
анықтауыштың j-тік жолын бос мүшелермен
алмастырғаннан пайда болған анықтауыш
болсын. Сонда, егер
 болса жүйенің жалғыз шешімі бар болады
және мынадай формуламен табылады:
болса жүйенің жалғыз шешімі бар болады
және мынадай формуламен табылады:
 (i=1,2,…,n)
формуланы
Крамер формуласы деп атайды. Осы ережені
қолданып мынадай жүйені шешейік
(i=1,2,…,n)
формуланы
Крамер формуласы деп атайды. Осы ережені
қолданып мынадай жүйені шешейік

Шешуі. Алдымен анықтауышты есептейміз,
 .т
(j=1,2,3)
анықтауыштарды есептейік
.т
(j=1,2,3)
анықтауыштарды есептейік
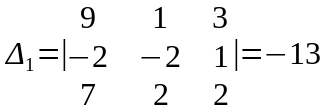 ,
,
 ,
,
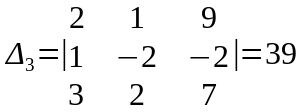
Енді Крамер формуласын қолданып белгісіздерді табамыз:
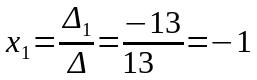 ,
,
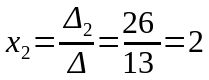 ,
,
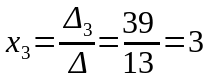 .
.
Сонымен, берілген жүйенің жалғыз (-1; 2; 3) шешімі табылды, жүйе анықталған екен.
5.Сызықты теңдеулерді шешу Гаусс әдісі
Гаусс
әдісі - жүйедегі айнымалыларды
түрлендірулер көмегімен біртіндеп
жойып, жүйені сатылы түрге келтіріп,
айнымалыларды біртіндеп табатын әдіс.
Гаусс түрлендірулері мынадай:Кез келген
екі теңдеудің орындарын ауыстырып жазу;
Кез келген теңдеудің екі жағын нолден
өзге санға көбейту; Қандай да бір теңдеуді
нолден өзге санға көбейтіп, басқа
теңдеуге сәйкесінше қосу; 0=0
түріндегі теңдеуді сызып тастау. Гаусс
түрлендірулерін жүйенің өзіне қолданғаннан
гөрі оның кеңейтілген матрицасына
қолданған ұтымды болады. Олай болса
жүйенің кеңейтілген матрицасын
қарастырайық,Жүйенің рангісі жүйедегі
белгісіздер санынан кем болса, онда
жүйе анықталмаған болатыны жоғарыда
айтылған. Айталық (6) жүйе үйлесімді
және r<n
болсын. Егер
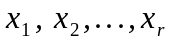 коэффициенттерінен құрылған анықтауыш
нолден өзгеше болса, онда
айнымалыларды базистік
(негізгі) айнымалылар
деп, ал басқа n-r
айнымалыларды еркін
(негізгі емес) айнымалылар
деп атайды. Еркін айнымалылары нолге
тең болған кездегі шешім базистік
шешім
деп аталады. Базистік шешімдер саны
коэффициенттерінен құрылған анықтауыш
нолден өзгеше болса, онда
айнымалыларды базистік
(негізгі) айнымалылар
деп, ал басқа n-r
айнымалыларды еркін
(негізгі емес) айнымалылар
деп атайды. Еркін айнымалылары нолге
тең болған кездегі шешім базистік
шешім
деп аталады. Базистік шешімдер саны
 -ден
артпайды Матрица рангісі 2-ге тең екенін
кеңейтілген матрицаға жүргізілген
түрлендірулерден кейін көру қиын емес,
сондықтан жүйедегі екі теңдеуді (мысалы,
бастапқы екеуін) қарастырамыз:
-ден
артпайды Матрица рангісі 2-ге тең екенін
кеңейтілген матрицаға жүргізілген
түрлендірулерден кейін көру қиын емес,
сондықтан жүйедегі екі теңдеуді (мысалы,
бастапқы екеуін) қарастырамыз: Олай
болса базистік шешімдері
Олай
болса базистік шешімдері
 дан артпайды. Базистік айнымалылар
ретінде мына айнымалылар жұбын алуға
болады
дан артпайды. Базистік айнымалылар
ретінде мына айнымалылар жұбын алуға
болады
 ,
, ;
,
;
, ;
,
;
, ;
,
;
,
,
.
Енді әрқайсысының базистік
айнымалылар бола алатынын немесе бола
алмайтынын білу үшін коэффициенттерінен
құрылған анықтауыштарды есептейміз.
Айталық
,
айнымалылар
коэффициенттеріне құрылған анықтауыш
;
,
;
,
,
.
Енді әрқайсысының базистік
айнымалылар бола алатынын немесе бола
алмайтынын білу үшін коэффициенттерінен
құрылған анықтауыштарды есептейміз.
Айталық
,
айнымалылар
коэффициенттеріне құрылған анықтауыш
 ,
олай болса бұлар базистік айнымалылар
бола алады. Базистік шешімді табу үшін
жүйедегі
,
айнымалыларды нолге теңестіреміз де
жүйені мына түрде жазамыз:
,
олай болса бұлар базистік айнымалылар
бола алады. Базистік шешімді табу үшін
жүйедегі
,
айнымалыларды нолге теңестіреміз де
жүйені мына түрде жазамыз:
 Бұл жүйенің шешімі:
Бұл жүйенің шешімі:
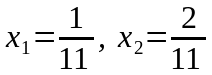 .
Сонда бастапқы жүйенің бір базистік
шешімі:
.
Сонда бастапқы жүйенің бір базистік
шешімі:
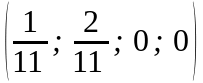 болады. Осы жолмен барлық
болады. Осы жолмен барлық
 ,
,
 ,
,
 ,
,
 ,
,
 базистік шешімдерді табамыз.4-мысал.
Біртекті
теңдеулер жүйесін шешейік,
базистік шешімдерді табамыз.4-мысал.
Біртекті
теңдеулер жүйесін шешейік,
 .
.
Шешуі.
Біртекті жүйе әруақытта үйлесімді,
себебі жүйенің
 нолдік шешуі бар. Ендік нолдік емес
шешулері бар жоқтығын анықтайық. Жүйенің
кеңейтілген матрицасын жазып, элементар
түрлендірулер жасайық:
нолдік шешуі бар. Ендік нолдік емес
шешулері бар жоқтығын анықтайық. Жүйенің
кеңейтілген матрицасын жазып, элементар
түрлендірулер жасайық:
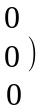







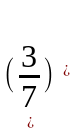

 Соңғы матрицаға сәйкес келетін
жүйе жазайық:
Соңғы матрицаға сәйкес келетін
жүйе жазайық: Осы
жүйеден
және
айнымалыларды табамыз:
Осы
жүйеден
және
айнымалыларды табамыз: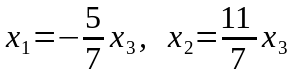
 деп
алсақ жүйе шешімі мынадай болады:
деп
алсақ жүйе шешімі мынадай болады:
 ,
.
,
.
