29) Дербес туынды. Екінші ретті дербес туындылар. Бағыт бойынша туынды. Градиент

Градиенттің қасиеттері. Скалярлық өрістің градиенті скалярлық функцияның дербес туындыларымен сипаттала-тындықтан туындының барлық қасиеттері градиент үшінде орындалады.

1. Екі функцияның қосындысының (айырмасының) градиенті ол функциялардың градиенттерінің қосындысына (айырмасына) тең:

.

Дәлелдеу. Анықтама бойынша

.

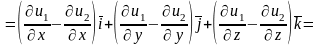
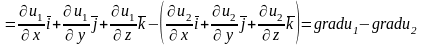2. Тұрақты көбейткішті градиент таңбасының алдына шығаруға болады:

.

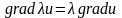3. Екі функцияның көбейтіндісінің градиенті мына формуламен табылады.

.

4. Екі функцияның қатынасының градиенті мына формуламен табылады:

.

Дербес туынды

Екінші ретті дербес туындылар.

   функциясының екінші ретті дербес туындысы – бірінші ретті дербес туындыларынан сәйкес айнымалылары бойынша туынды табу:

 туындыларын аралас туындылар деп атайды. Үзіліссіз болған кезде олар өзара тең болады.

 функциясының екінші ретті дербес туындысын табу алгоритмі.

1. 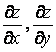  бірінші ретті дербес туындыларды   есептеу.

2. Табылған   туындысындағы   айнымалысын бекітіп,   айнымалысы бойынша туынды тауып,   аламыз.

3. Табылған   туындысындағы    айнымалысын бекітіп,   айнымалысы бойынша туынды тауып,   аламыз.

Мысал 1:

 функциясының екінші ретті дербес туындылары келесі өрнектерге тең: 

30) Екі айнымалды функ-ның экстремумы. Экстремумының қажетті шарттары.

Егер М₀( х₀ у₀ ) Hүктесі үшін Ɏ М (x,y)€U(М₀), f(х,у)≤f(х_0, у₀) (f(x,y)≥f(x_Q;y_Q)) теңсіздігі орындалатындай U(М₀) маңайы табылса, онда z=f(x;y) функциясының М₀(х₀,у₀) нуктесінде (локальдік) төңіректік максимумы (минимумы) бар дейді.

М₀(х₀;у₀) нуктесін төңіректік максимум (минимум) нуктесі, ал функцияның осы нуктеден мәнін функцияның төңіректік максимум (минимум) мәні деп атайды. Төңіректік максимум мен төңіректік минимум мәндері — төңіректік экстремум деп аталады.

Төңіректік экстремумның кажетті шарты:

Егер дифференциалданатын z=f(х.y) функциясының М₀(х₀;у₀) нуктесінде төңіректік экстремумы бар болса, онда оның осы нуктедегі дербес туындылары нольге тең:

Z_x’(х_0, у₀) =0 Z_y’(х_0, у₀) =0 (8.26)

Дифференциал мен градиент анықтамасынан келесі тұжырым шығады: М₀(х₀;у₀) нуктесінде дифференциалданатын z=f(x;y) функциясының осы нуктеде төңіректік экстремумы бар болса, онда df(M₀) = О немесе gradf(M₀)=0. (8.27)

M_Q(x_Q;y₀) нуктесінде (8.26) шарттар орындалса, онда М₀ нүктесі f(x;y) функциясының стационар нуктесі деп аталады.f(х;у) функциясының стационар нуктелері мен оның дифференциалданбайтын нуктелерін күдікті нуктелер деп атайды.

Мысалы, z = х² +у² <=(түбір астында) функциясы O(0;0) нүктесінде минимум мәнін қабылдайды, бірақ бұл нүктеде функция дифференциалданбайды. Әрбір стационар нүкте локальдік экстремум нүктесі бола алмайды.

31)Екі айнымалды функ-ның экстремумы. Жеткілікті шарттары.

Егер М₀( х₀ у₀ ) Hүктесі үшін Ɏ М (x,y)€U(М₀), f(х,у)≤f(х_0, у₀) (f(x,y)≥f(x_Q;y_Q)) теңсіздігі орындалатындай U(М₀) маңайы табылса, онда z=f(x;y) функциясының М₀(х₀,у₀) нуктесінде (локальдік) төңіректік максимумы (минимумы) бар дейді.

М₀(х₀;у₀) нуктесін төңіректік максимум (минимум) нуктесі, ал функцияның осы нуктеден мәнін функцияның төңіректік максимум (минимум) мәні деп атайды. Төңіректік максимум мен төңіректік минимум мәндері — төңіректік экстремум деп аталады.

Төңіректік экстремумның жеткілікті шарты: z=f(x,y) функциясы М₀(х₀;у₀) стационар нүктесінің кейбір U(M₀) манайында екі рет дифференциалданатын жене онын екінші ретті дербес туындылары М₍₎(х₀;у₀) нуктесінде үзіліссіз болсын,

А=f’’_xx(x_Q;y_Q). В =f’’_xy(х₀,у₀),С =f’’_yy(х₀,у₀), ∆ =AС-В²:

1. Eгер ∆ >0 болса, онда М₀(х₀,у₀) нүктесінде f(x,y) функциясының төңіретік экстремумы бар, атап айтқанда, À<0 (С<0), болса – төңіректік, À>0 (С>0)болса - төңіректік минимум мәнін қабылдайды.

2. А<0 болса, онда нуктесінде М₀(х₀,у₀) функциясының төңіректік экстремумы жок;

3. ∆=0 болса, онда f(x,у) функциясының М₀(х₀,у₀) нуктесіндегі сипаты оның екіден жоғары ретті дифференциалымен анықталады. (Төңіректік экстремум болуы да, болмауы да мумкін)