27) Екі айнымалды тәуелді функция және оның анықталу облысы, графигі.

D облысынан алынған х_{1 ,} x_{2, …,}x_n сандарына U облысының тек қана бір u саны f  заңдылығы бойынша сәйкестікке қойылса, онда D  облысында  =f(х_{1 ,} x_{2 …}x_n) функциясы берілген дейміз. Екі айнымалы  функцияның анықталу облысы  жазықтықтағы қандай да бір фигураны немесе жазықтықтың бір бөлігін білдіреді. Ал үш айнымалы функцияларда анықталу облысы кеңістіктегі қандай да бір денені білдіреді.

  Мысалы:

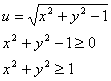   шардың теңдеуі

 

 

Мысалы:

 Сфераның теңдеуі

 

 

 Z=f(x,y) Функцияның х бойынша дербес туындысы деп

 

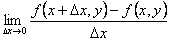 қатынасының ақырлы шегін айтамыз.

 

Z=f(x,y) функцияның у бойынша дербес туындысы деп

 

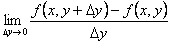қатынасының ақырлы шегін айтамыз.

 

Z=f(x,y)  функциясының х  бойынша дербес туындысы 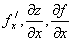 ,   арқылы, ал

 

у  бойынша дербес туындысы 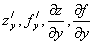  арқылы белгіленеді.

Мысалы:

 

 

 

 

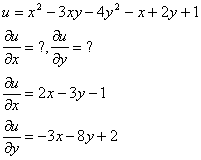
Z=f(x,y)  функцияның М(х,у) нүктесіндегі толық өсімшесі деп  айырымын айтамыз. Мұндағы   пен  аргументтер өсімшесі.

Z=f(x,y)   функциясы  М нүктесінде дифференциалданады, егер осы нүктеде  функцияның толық өсімшесін   түрінде жазуға болса мұндағы  ,  .

Z=f(x,y)   функциясының толық дифференциалы деп   толық өсімшесінің    және   - ке  қатысты сызықты негізгі бөлігін айтамыз. Яғни 

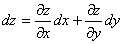
Мысалы:

 

 

 

Жуықтап есептеу формуласы: 

Мысалы:

28) Екі айнымалды функ-ның шегі.

ХоУ жазықтығында 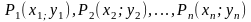(1) нүктелер тізбегін қарастырайық.

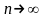
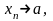
Егер 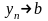болса, онда (1) тізбегі 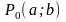нүктесіне жинақталады деп айтады.

z=f(x;y) функциясы нүктесінің манайында анықталған болсын.

Анықтама: егер z=f(x;y) үшін D аймағындағы нүктелердің кез келген тізбегі 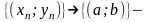да оларға сәйкес f(x;y) функциясының мәндерінің тізбегі 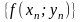бір ғана А санына ұмтылатын болса, онда А саны z=f(x;y) функциясының 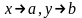-ға ұмтылғандағы шегі деп аталады да былай белгіленеді:

Анықтама: егер z=f(x;y) функциясы нүктесінде анықталып

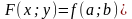болса, онда ол нүктесінде үзіліссіз деп аталады.

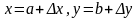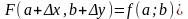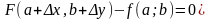
Егер деп белгілесек, онда (2) теңдеу келесі түрде жазылады: немесе (3)

(3) теңдіктегі тік жақшадағы өрнек z функциясының негізгі 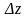өсімшесі болғандықтан 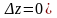(4) болады.

Сонымен, егер нүктесінде аргументтердің ақырсыз кіші 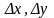өсімшелеріне z=f(x;y) функциясының ақырсыз кіші өсімшесі сәйкес болса, онда z=f(x;y) функциясы нүктесінде үзіліссіз деп аталады.

D аймағының әрбір нүктесінде үзіліссіз болатын функция сол аймақта үзіліссіз деп аталады.

Егер бір нүктелерде функцияның үздіксіз шарттары орындалмаса, онда олар үзіліс нүктелері деп аталады.

1 Мысал: функциясы ХоУ жазықтығында үзіліссіз екенін көрсету керек.

Δ функцияның өсімшесін анықтайық:

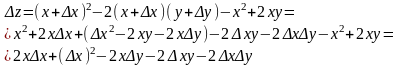
кез келген болғандықтан берілген функция ХОУ жазықтығының барлығында үзіліссіз. ▲

2 Мысал: функциясын үздіксіздікке зерттеу керек.

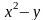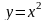Δ және функциялары ХОУ жазықтығының әрбір нүктесінде үзіліссіз. Ал берілген функция нүктелерінде үзіледі. Сондықтан, z функциясы ХОУ жазықтығының параболасында орналасқан нүктелерден басқа әрбір нүктеде үзіліссіз.▲