
- •Жиындар және оларға амалдар қолдану. Нақты сандар жиыны
- •2.Анықтауыштар және олардың қасиеттері. Анықтауыштарды есептеу. Мионер және алгебралық толықтауыш.
- •3)Матрица және оларға қолданылатын амалдар. Кері матрица.
- •4)Сызықты теңдеулер жүйесі. Крамер ережесі.
- •5.Сызықты теңдеулерді шешу Гаусс әдісі
- •6. Жазықтықтағы сызық теңдеуі. Түзудің әртүрлі теңдеулері, бұрыштың коэффициеттік теңдеуі.
- •7)Түзудің нормалдық теңдеуі. Нүктеден түзуге дейінгі қашықтық.
- •8.Екінші ретті сызықтар: шеңбер, эллипс, гипербола, парабола
- •9. Жазықтықтың жалпы теңдеуі және оны зерттеу.
- •10. Кеңістіктегі түзу және оның әртүрлі теңдеулері.
- •11.Анықталмаған интеграл және оның қасиеттері. Интегралдар кестесі.
- •12. Анықталмаған интегралды табу әдістері: тікелей интегралдау, айнымалдарды алмастыру әдісі.
- •13. Анықталмаған интегралды табу: бөліктеп интегралдау әдісі.
- •14. Рационал бөлшектерді интегралдау.
- •15. Анықталған интеграл және оның қасиеттері. Ньютон-Лейбинц формуласы
- •16) Бірінші және екінші текті меншіксіз интегралдар.
- •17) Функ-ның нүктедегі шегі. Бір жақты шектер. Функ-ның шектері туралы теорема.
- •18) Ақырсыз кішкене және ақырсыз үлкен шамалар. Ақырсыз шамаларды салыстыру.
- •19) Үзіліссіз функцияның негізгі қасиеттері.
- •20) Туынды ұғымы. Туындының геометриялық және механикалық мағыналары. Туынды табудың негізгі ережелері. Қарапайым функ-дың туындылары. Қосындыны, көбейтіндіні, бөліндіні дифференциалдау ережелері.
- •21) Функцияның дифференциалы. Дифференциалдың жуықтап есептеулерде қолданылуы.
- •22) Күрделі функция және оның туындысы. Кері функция және оның туындысы. Логарифмдік туынды
- •23) Жоғарғы ретті туындылар мен жоғарғы ретті дифференциалдар. 2-ретті туындының физикалық мағынасы.
- •24) Анықталмағандықтарды Лопиталь ережесі арқылы шешу.
- •25) Функцияның өсуі мен кемуі. Функцияның локалдық экстремумы. Функцияның экстремумының қажетті шарты.
- •26) Функцияның экстремумының жеткілікті шарттары. Қисықтың ойыстығы мен дөңестігінің иілу нүктелері. Қисықтың асимптоталары.
- •27) Екі айнымалды тәуелді функция және оның анықталу облысы, графигі.
- •28) Екі айнымалды функ-ның шегі.
- •29) Дербес туынды. Екінші ретті дербес туындылар. Бағыт бойынша туынды. Градиент
- •30) Екі айнымалды функ-ның экстремумы. Экстремумының қажетті шарттары.
- •32)Ықтималдықтың классикалық анықтамасы
21) Функцияның дифференциалы. Дифференциалдың жуықтап есептеулерде қолданылуы.
![]() функциясының
шектелген туындысы бар болсын, онда:
функциясының
шектелген туындысы бар болсын, онда:
![]() ,
демек
,
демек
![]()
![]() шексіз
аз шама.
шексіз
аз шама.
Онда
функцияның өсімшесі былай жазылады:
![]() .
Осы теңдікте екінші қосылғыш
.
Осы теңдікте екінші қосылғыш
![]() ,
,
![]() ке
қарағанда жоғарғы ретті шексіз аз шама
болғандықтан, бірінші қосылғыш
ке
қарағанда жоғарғы ретті шексіз аз шама
болғандықтан, бірінші қосылғыш
![]() ке
эквивалентті шама болады.
ке
эквивалентті шама болады.
Анықтама.
Функцияның
туындысының аргументтің өсімшесіне
көбейтіндісін дифференциал деп атайды
және мына түрде жазады:
![]() .
Дербес жағдайда, егер
.
Дербес жағдайда, егер
![]() болса, онда
болса, онда
![]() ,
осыдан
,
осыдан
![]() және осыны пайдаланып дифференциалдың
формуласын былай жазуға болады:
және осыны пайдаланып дифференциалдың
формуласын былай жазуға болады:
![]() .
Осыдан
.
Осыдан
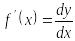 ,
яғни туынды функцияның дифференциалының
аргумент дифференциалына бөлінген
мәніне тең.
,
яғни туынды функцияның дифференциалының
аргумент дифференциалына бөлінген
мәніне тең.
![]() берілген
функциясының
бірінші немесе бірінші ретті туындысы,
ал функцияның өзі нөлінші ретті туынды
деп аталады.
берілген
функциясының
бірінші немесе бірінші ретті туындысы,
ал функцияның өзі нөлінші ретті туынды
деп аталады.
Анықтама.
Функцияның
–ші
ретті туындысы деп оның (
-1)-ші
туындысының туындысын айтады
![]() ,
=1,2,3,…,
егер
олар бар болса, онда
,
=1,2,3,…,
егер
олар бар болса, онда
![]() функциясы
функциясы
![]() -рет
дифференциалданатын функция деп
аталады.
-рет
дифференциалданатын функция деп
аталады.
Мысал.
![]() функциясы
берілген. Бірінші туындысы
функциясы
берілген. Бірінші туындысы
![]() ,
екінші туындысы
,
екінші туындысы
![]() ,
үшінші туындысы
,
үшінші туындысы
![]() .
Демек,
.
Демек,
![]() ,
,
![]() .
Егер
және
.
Егер
және
![]() функциялары
–рет
дифференциалданатын
болса, онда
(
функциялары
–рет
дифференциалданатын
болса, онда
(![]() ),
мына ережелер орынды:
),
мына ережелер орынды:
![]() ,
,
![]() .
.
Дифференциалды
есептеу ережесі. Айталық
![]() және
және
![]() дифференциалданатын функциялар болсын,
дифференциалданатын функциялар болсын,
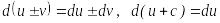 ,
мұндағы
с
–сан.
,
мұндағы
с
–сан.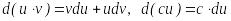 ,
,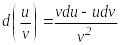 ,
егер
,
егер
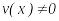 .
.Егер
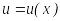 функциясы
нүктесінде дифференциалданатын,
ал
функциясы
нүктесінде дифференциалданатын,
ал
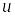 нүктесінде дифференциалданатын болса,
онда
нүктесінде дифференциалданатын болса,
онда
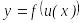 күрделі
функция үшін,
күрделі
функция үшін,
 .
Бұл ережені бірінші
дифференциал формасының инварианттығы
деп атайды. Дифференциалды жуықтап
есептеуге қолдануға болады. Айталық,
функциясы
дифференциалданатын болсын, онда оның
өсімшесі:
.
Бұл ережені бірінші
дифференциал формасының инварианттығы
деп атайды. Дифференциалды жуықтап
есептеуге қолдануға болады. Айталық,
функциясы
дифференциалданатын болсын, онда оның
өсімшесі:
,
осыдан
![]()
![]() .
.
Егер
![]() нүктесінде функцияның мәні берілсе,
онда:
нүктесінде функцияның мәні берілсе,
онда:
![]() .
.
мысал.
![]() -ты
жуықтап есепте.
-ты
жуықтап есепте.

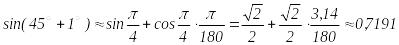 .
.
22) Күрделі функция және оның туындысы. Кері функция және оның туындысы. Логарифмдік туынды
Күрделі
функцияның туындысы.
![]() функциялары үзіліссіз және
дифференциалданатын функциялар болсын.
Сонда күрделі
функциялары үзіліссіз және
дифференциалданатын функциялар болсын.
Сонда күрделі
![]() функциясының туындысы:
функциясының туындысы:
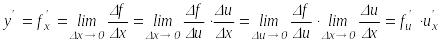 .
Сонымен
.
Сонымен
![]() .
.
мысал.
![]()
![]() туындысын
табу керек. Функцияны былай жазамыз
туындысын
табу керек. Функцияны былай жазамыз
![]() ,
мұндағы
,
мұндағы
![]() .
Сондықтан
.
Сондықтан
![]() .
.
мысал.
![]() туындысын табу керек.
туындысын табу керек.
![]() .
.
Кері
функцияның туындысы.
![]() және оған кері
және оған кері
![]() функциялары
функциялары
![]() кесіндісінде үзіліссіз және
дифференциалданатын болсын. Сонда кері
функцияның туындысы:
кесіндісінде үзіліссіз және
дифференциалданатын болсын. Сонда кері
функцияның туындысы:
 .
Сонымен
.
Сонымен
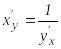 болады.
болады.
мысал.
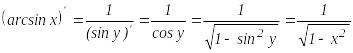 .
.
Мұнда
![]() .
.
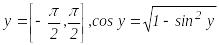 .
.
мысал.
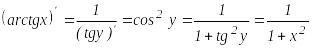 .
.
23) Жоғарғы ретті туындылар мен жоғарғы ретті дифференциалдар. 2-ретті туындының физикалық мағынасы.
берілген функциясының бірінші немесе бірінші ретті туындысы, ал функцияның өзі нөлінші ретті туынды деп аталады.
Анықтама. Функцияның –ші ретті туындысы деп оның ( -1)-ші туындысының туындысын айтады , =1,2,3,…, егер олар бар болса, онда функциясы -рет дифференциалданатын функция деп аталады.
Мысал. функциясы берілген. Бірінші туындысы , екінші туындысы , үшінші туындысы . Демек, , . Егер және функциялары –рет дифференциалданатын болса, онда ( ), мына ережелер орынды: , .
2. Лейбниц формуласы:
![]()
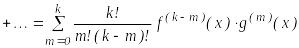 ;
;
![]() .
.
Айталық функциясы –рет дифференциалданатын болсын.
Анықтама.
Функцияның
–ші
дифференциалы деп оның (![]() )–ші
ретті дифференциалының дифференциалын
айтады:
)–ші
ретті дифференциалының дифференциалын
айтады:
![]() .
.
Дифференциалды есептеу формулаларын келтірейік:
![]() ,
,
![]() ,
,
![]() ,
,
… … … … … … … … … … … … … … …
![]() .
–шы
ретті дифференциалдар үшін мына ережелер
орынды:
.
–шы
ретті дифференциалдар үшін мына ережелер
орынды:
1)
![]() ,
,
![]() .
.
2)
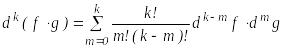 ,
,
![]() .
.
Ескерту:
Жоғарғы ретті
![]() дифференциал формасы инвариантты емес.
дифференциал формасы инвариантты емес.
Дифференциалдық есептеулердің негізгі теоремалары
Анықтама.
Егер
нүктесінің бір маңайында
![]()
![]() теңсіздігі орындалса, онда
нүктесін
функциясының жергілікті минимум
(максимум) нүктесі деп атайды. Жергілікті
минимум және жергілікті максимум
нүктелері жергілікті экстремум нүктелері
деп аталады. Ал осы нүктелердегі
функцияның мәні функцияның экстремумы
деп аталады.
теңсіздігі орындалса, онда
нүктесін
функциясының жергілікті минимум
(максимум) нүктесі деп атайды. Жергілікті
минимум және жергілікті максимум
нүктелері жергілікті экстремум нүктелері
деп аталады. Ал осы нүктелердегі
функцияның мәні функцияның экстремумы
деп аталады.
![]() кесіндісінде анықталған функцияның
тек қана бір ең үлкен және ең кіші мәндері
болады, ал максимумдар және минимумдер
бірнеше болуы мүмкін. Функцияның кейбір
максимумдары оның минимумдарынан кіші
болуы да мүмкін.
кесіндісінде анықталған функцияның
тек қана бір ең үлкен және ең кіші мәндері
болады, ал максимумдар және минимумдер
бірнеше болуы мүмкін. Функцияның кейбір
максимумдары оның минимумдарынан кіші
болуы да мүмкін.
Ферма
теоремасы. Егер
функциясы
интервалында дифференциалданатын болса
және
![]() нүктесінде ең үлкен немесе ең кіші мәнін
қабылдайтын болса, онда функцияның
туындысы бұл нүктеде нөлге тең, яғни
нүктесінде ең үлкен немесе ең кіші мәнін
қабылдайтын болса, онда функцияның
туындысы бұл нүктеде нөлге тең, яғни
![]() .
.
Геометриялық мағынасы: функцияның максимум және минимум нүктелерінде жүргізілген жанама өсіне параллель болады.
Ролль
теоремасы.
Егер
![]() функциясы:
функциясы:
![]() кесіндісінде үзіліссіз болса,
интервалында дифференциалданатын болса
және
кесіндісінде үзіліссіз болса,
интервалында дифференциалданатын болса
және
![]() болса,
онда ең болмағанда бір
болса,
онда ең болмағанда бір
![]() нүктесі табылып,
нүктесі табылып,
![]() болады.
болады.
Геометриялық мағынасы: егер теорема шарттары толығымен орындалса, онда кесіндісінде жататын ең болмағанда бір нүктесі табылып, сол нүктеде жүргізілген жанама өсіне параллель болады.
Kоши
теоремасы.
Егер
және
функциялары
кесіндісінде үзіліссіз болса,
интервалында дифференциалданатын болса
және
![]()
![]() ,
онда ең болмағанда бір
нүктесі табылып
,
онда ең болмағанда бір
нүктесі табылып
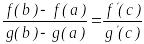 теңдігі
орындалады.
теңдігі
орындалады.
Лагранж
теоремасы.
Егер
функциясы
кесіндісінде үзіліссіз болса,
интервалында дифференциалданатын болса
онда
![]() интервалында
жататын
интервалында
жататын
![]() нүктесі табылып,
нүктесі табылып,
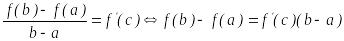 теңдігі
орындалады.
теңдігі
орындалады.
Геометриялық
мағынасы: мына
қатынас
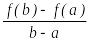 кесіндісінде
функциясының графигінің шеткі нүктелерін
қосатын хорданың
кесіндісінде
функциясының графигінің шеткі нүктелерін
қосатын хорданың
![]() өсінің
оң бағытымен жасайтын бұрыштың тангесіне
тең, ал
өсінің
оң бағытымен жасайтын бұрыштың тангесіне
тең, ал
![]() нүктесіне жүргізілген жанаманың
өсінің оң бағытымен жасайтын бұрышының
тангенісіне тең. Лагранж теоремасы
бойынша
нүктесінде олар өзара тең болады, яғни
қиюшы мен жанама параллель болады.
нүктесіне жүргізілген жанаманың
өсінің оң бағытымен жасайтын бұрышының
тангенісіне тең. Лагранж теоремасы
бойынша
нүктесінде олар өзара тең болады, яғни
қиюшы мен жанама параллель болады.
