16) Бірінші және екінші текті меншіксіз интегралдар.

Бірінші және Екінші тек-тi меншіксіз интегралдар. Біз осыган дейін анықталган интегралдар туралы айтканда ннтегралдау аралыгы шектелген және интеграл астындагы функция осы аралыкта шенелген деп кабылдадык. БipaK аныкталган интеграл аныктамасын шексіз интегралдау аралыгы ушин және шенелмеген функция жагдайына арнап зерттеу кажеттігі жиі кездеседі. Енді осы сұрактарды карастырайык:

I. а) ф функциясы [а, ) аралыгында берілсін;

б) ф- кез келген акырлы [a,b ] кесіндісінде (мұндағы b' )) интегралданатын болсын.

Егер

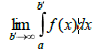
болса, онда ол шек f функциясының [a, )

аралығындағы (бірінші текті) меншіксіз интегралы деп аталады да келесі

түрде белгіленеді:

II. а) f - шекті [a,b) аралығында берілген және b- нүктесінің маңайында шенелмеген функция;

б) f - кез келген [a,b ] кесіндісінде (a<b’<b) интегралданатын

функция болсын.

Егер

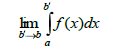
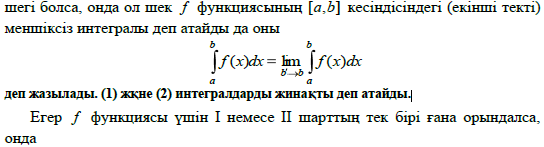
17) Функ-ның нүктедегі шегі. Бір жақты шектер. Функ-ның шектері туралы теорема.

Шек экономикада көптеген шамалардың орташа мәндерін қарастырады. Мысалы, орташа шығын, орташа табыс, орташа пайда, т.с.с. Сонымен қатар, қандай да бір шаманы көбейткенде немесе азайтқанда нәтиже қаншалықты өзгеретіндігін білу үшін математиканың шектік талдау әдісін қолдану керек болады. Егер алдын ала берілген, мейілінше аз санына саны табылып, шартын қанағаттандыратын барлық х үшін теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х₀-ге ұмтылғандағы шегі деп аталады да, былай жазылады: .Функция шегінің қасиеттері. Айталық және функцияларының жағдайда және шектері бар болсын..1)Екі функцияның алгебралық қосындысының шегі шектердің алгебралық қосындысына тең болады, яғни = .2)Екі функцияның көбейтіндісінің шегі шектердің көбейтіндісіне тең болады, яғни = .3)Екі функцияның қатынасының шегі шектердің қатынасына тең болады (әрине, егер бөлімдегі функция нолден өзгеше болса), яғни

= . функциясы x=0 нүктеде анықталмаған, бірақ жағдайда шегі бар және Осы шекті бірінші тамаша шек деп атайды.Бірінші тамаша шек салдары:

1) ,2) , 3) .

Мысал. . функциясының жағдайда шегі бар және Осы шекті екінші тамаша шек деп атайды.Екінші тамаша шек салдары:

1) ,a=e болғанда ;

2) , a=e болғанда ;

Мысал. екенін көрсет.

Шешуі. деген білгілеу енгізейік. Осыдан . Және де кезде . Енді шек есептесек

.

18) Ақырсыз кішкене және ақырсыз үлкен шамалар. Ақырсыз шамаларды салыстыру.

функциясының жағдайда шегі ноль болса, яғни , онда функциясы жағдайда ақырсыз аз функция деп аталады.Ақырсыз аз функция қасиеттері.1)Егер функциясының жағдайда А шегі бар болса, онда функциясын осы А саны мен жағдайда ақырсыз аз болатын функция қосындысы түрінде жазуға болады, яғни .2)Ақырсыз аз функцияның шенелген функцияға (сонмен қатар, тұрақтыға, басқа ақырсыз азға) көбейтіндісі ақырсыз аз функция болады.3)Ақырсыз аз функцияның шегі нолден өзге функцияға қатынасы ақырсыз аз функция болады. функциясының жағдайда шегі шексіздік болса, яғни , онда функциясы жағдайда ақырсыз үлкен функция деп аталады.Ақырсыз аз функция мен ақырсыз үлкен функция арасында мынадай байланыс бар: Егер функциясы жағдайда ақырсыз аз болса, функциясы жағдайда ақырсыз үлкен болады. Ақырсыз аздарды салыстыру үшін олардың қатынасының жағдайдағы шегін қарастырады.Айталық және жағдайда ақырсыз аз функциялар және болсын. Онда, егер1) болса -ға қарағанда жоғары ретті ақырсыз аз деп;2) болса мен бірдей ретті ақырсыз аз деп;3) болса мен эквивалентті ақырсыз аз деп аталады.

, .