1. Жиындар және оларға амалдар қолдану. Нақты сандар жиыны

2. Анықтауыштар және олардың қасиеттері. Анықтауыштарды есептеу. Минор және алгебралық толықтауыш.

3. Матрица және оларға қолданылатын амалдар. Кері матрица.

4. Сызықты теңдеулер жүйесі. Крамер ережесі.

5. Сызықты теңдеулерді шешу Гаусс әдісі

6. Жазықтықтағы сызық теңдеуі. Түзудің әртүрлі теңдеулері, бұрыштың коэффициеттік теңдеуі.

7. Түзудің нормалдық теңдеуі. Нүктеден түзуге дейінгі қашықтық.

8. Екінші ретті сызықтар: шеңбер, эллипс, гипербола, парабола

9. Жазықтықтың жалпы теңдеуі және оны зерттеу.

10. Кеңістіктегі түзу және оның әртүрлі теңдеулері.

11. Анықталмаған интеграл және оның қасиеттері. Интегралдар кестесі.

12. Анықталмаған интегралды табу әдістері: тікелей интегралдау, айнымалдарды алмастыру әдісі.

13. Анықталмаған интегралды табу: бөліктеп интегралдау әдісі.

14. Рационал бөлшектерді интегралдау.

15. Анықталған интеграл және оның қасиеттері. Ньютон-Лейбинц формуласы

16. Бірінші және екінші текті меншіксіз интегралдар.

17. Функ-ның нүктедегі шегі. Бір жақты шектер. Функ-ның шектері туралы теорема.

18. Ақырсыз кішкене және ақырсыз үлкен шамалар. Ақырсыз шамаларды салыстыру.

19. Үзіліссіз функцияның негізгі қасиеттері.

20. Туынды ұғымы. Туындының геометриялық және механикалық мағыналары. Туынды табудың негізгі ережелері. Қарапайым функ-дың туындылары. Қосындыны, көбейтіндіні, бөліндіні дифференциалдау ережелері.

21. Функцияның дифференциалы. Дифференциалдың жуықтап есептеулерде қолданылуы.

22. Күрделі функция және оның туындысы. Кері функция және оның туындысы. Логарифмдік туынды

23. Жоғарғы ретті туындылар мен жоғарғы ретті дифференциалдар. 2-ретті туындының физикалық мағынасы.

24. Анықталмағандықтарды Лопиталь ережесі арқылы шешу.

25. Функцияның өсуі мен кемуі. Функцияның локалдық экстремумы. Функцияның экстремумының қажетті шарты.

26. Функцияның экстремумының жеткілікті шарттары. Қисықтың ойыстығы мен дөңестігінің иілу нүктелері. Қисықтың асимптоталары.

27. Екі айнымалды тәуелді функция және оның анықталу облысы, графигі.

28. Екі айнымалды функ-ның шегі.

29. Дербес туынды. Екінші ретті дербес туындылар. Бағыт бойынша туынды. Градиент

30. Екі айнымалды функ-ның экстремумы. экстремумының қажетті шарттары.

31. Екі айнымалды функ-ның экстремумы. Жеткілікті шарттары.

32. Ықтималдықтың классикалық анықтамасы

1. Жиындар және оларға амалдар қолдану. Нақты сандар жиыны

Жиын – белгілі қасиеттері бойынша дәл анықталған табиғаты әр түрлі объектілер топтамасы. Жиынды құраушы объектілер жиынның элементтері деп аталады. Егер х элементі А жиынына тиісті болса, онда хЄА деп, ал егер у элементі А жиынына тиісті болмаса, онда у€А деп жазады. Бірде бір элементі жоқ жиынды бос жиын деп атайды да Ø таңбасымен белгілейді.

Егер А жиынының барлық элементтері Вжиынының да элемметтері болса, Ажиынын Вжиынының ішжиыны дейді де, АﺡВ немесе ВכּА деп белгілейді, ал егер А мен Вжиындары бірдей элементтерден тұрса, әрі АﺡВ және ВכּА болса, онда бұл жиындар тең, яғни А=Вдейді. А мен Вжиындарынын ортақ элемееттерінен

Тұратын жиынды олардың қиылысуы деп атайды да, А∩В таңбасымен белгілейді. Егер жиындардың ортақ элементтері жоқ болса, онда олардың қиылысуы бос жиын, яғни А∩В=Ø болады.А мен В жиындарының кемінде бipeyіндe жататын элементтерден тұратын жиынды олардың бipiгyi деп, ал осы жиындардың біpeyi А-ның екіншісі В-да жатпайтын элементерден тұратын жиынды олардың 6ipiгyi деп, ал осы жиындардын 6ipeyi А—ның eкіншіci В-да жатпайтын элементтерден туратын жнынды олардың айырмасы деп атайды да, сәйкес AUВ және А\Вдеп белгілейді.

Егер AﺡВ немесе А=Вболса, онда А\В=Ø. А және В жиындарының кебейтінд АхВ деп барлық х, у жұптардың, мұнда хЄА, уЄВ жиынын атайды да, F=AxB деп белгілейді.

А жиынынын S жиынға сейкес АﺡS толыкдауышы деп А=S\ А жиынды атайды.

Егер А₁UA₂U... U A_n =А және А_i∩А_j =Ø, i≠j, i,j=1,2,...,n, болса онда А_1,A_2,...,A_n ішжиындарын А жиынының бөліктеуі дейді. Жиындар екі турлі тәсілмен беріледі:

а) А жиынының барлық элементтері х₁,x₂…x_n тізімделеді де, А={х₁,x₂…x_n} деп жазылады;

б) А жиынын негізгі жиын Х-тің α(х) қасиетке ие болушы элементтерімен анықталады да, А={x€X| α(х)} деп жазылады. N={1,2,3,…,n,…} – натурал сандар жиыны, Z={…,-3,-2,-1,0,1,2…} бүтін сандар жиыны, ={0,1,2,…,n,…} теріс емес бүтін сандар жиыны.

2.Анықтауыштар және олардың қасиеттері. Анықтауыштарды есептеу. Мионер және алгебралық толықтауыш.

Квадрат матрицаны сипаттауға қажетті анықтауыш ұғымын енгізейік. Екінші ретті матрицаның 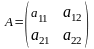анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады: Мысалы, матрицаның анықтауышын есептейік: . Ал үшінші ретті матрицаға үшінші ретті анықтауыш сәйкес келеді: Бұл анықтауыштың есептелуін үшбұрыш ережесі немесе Саррус ережесімен оңай есте сақтауға болады. Мысалы, мынадай үшінші ретті анықтауышты есептейік: Реті болатын анықтауыштарды есептеу үшін жаңа ұғымдар қажет болады Енді анықтауыш қасиеттерін қарастырайық.

1-қасиет. Анықтауыштың жатық жолдарын сәкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен, анықтауыш мәні өзгермейді:

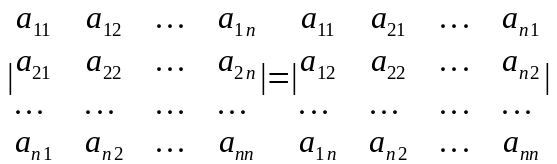
Теңдіктің дұрыстығын анықтауыштарды есептеу арқылы тексеруге болады.

2-қасиет. Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. Үшінші ретті анықтауыштың екінші жолындағы ортақ көбейткішті анықтауыш алдына шығарамыз:

.

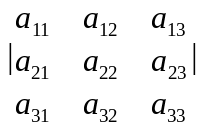Теңдіктің дұрыстығына берілген матрицаны екінші жол бойынша жіктеп тексеруге болады.

3-қасиет. Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. Үшінші ретті анықтауыштың бірінші және екінші жолдарын алмастырайық:

Теңдіктің дұрыстығын екінші анықтауышты бірінші жол бойынша жіктеп тексеруге болады.

4-қасиет. Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нолге тең. Үшінші ретті анықтауыштың бірінші және екінші жолдары бірдей болсын:

=0.

Теңдіктің дұрыстығын осы екі жолдың орндарын алмастырып 3-қасиетті қолданып тексеруге болады.

5-қасиет. Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді. Үшінші ретті анықтауыштың бірінші жолын 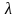-ға көбейтіп екінші жолға қосайық:

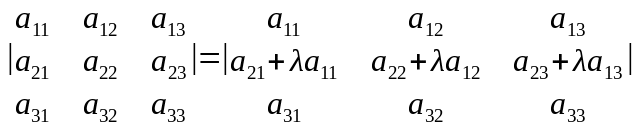.Теңдіктің дүрыстығын екінші анықтауышты мынадай + анықтауыштардың қосындысы түрінде жазайық. Сонда бірінші қосылғыш берілген анықтауыш болады да, екінші анықтауыш нолге тең.

6-қасиет. Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісіне тең: .

Теңдіктің дұрыстығын анықтауышты бірінші тік немесе үшінші жатық жол бойынша жіктеп тексеруге болады.

Осы қасиеттер көмегімен жоғары ретті анықтауыштар есептеуді көп жеңілдетуге болады. Анықтауышты қандай да бір жолында неғұрлым көп ноль болатындай етіп түрлендіріп, сол жол бойынша жіктеп анықтауыш реті төмендетіледі.

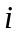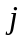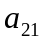Анықтама. n-ретті квадрат матрицаның –жатық жолы мен –тік жолын сызып тастағаннан кейін пайда болған (n–1)-ретті анықтауықты элементінің миноры деп атайды және деп белгілейді. Үшінші ретті марицаның элементінің миноры мынадай екінші ретті анықтауыш болады:

элементінің алгебралық толықтауышы деп мынадай санды айтады: Үшінші ретті марицаның элементінің алгебралық толықтауышы мынадай сан:

Мысалы, матрицасының бірінші жатық жолдағы элементтерінің миноры мен алгебралық толықтауыштарын есептейік: , , ,

, ,

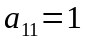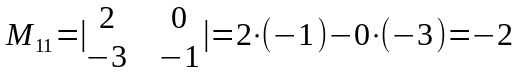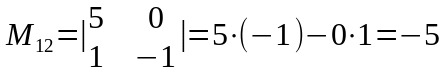
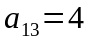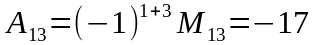, , . mxn өлшемді А матрицаның бірнеше жатық және тік жолдарын сызып тастап k өлшеміді, k min(m,n), квадрат матрица алуға болады. Осы квадрат матрица анықтауышы берілген матрицаның k өлшемді миноры деп аталады. матрицаның k-өлшемді минорлар саны 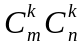болады.