1. Оцінка математичного сподівання

Для незгрупованої вибірки вибірковим середнім називають статистику

. (4.2)

Для згрупованої вибірки вибірковим середнім називають статистику

(4.3)

(тут - середні точки інтервалів групування;

- абсолютні частоти цих інтервалів).

Вибіркове середнє використовується як оцінка теоретичного математичного сподівання Мξ. Величина , обчислена за формулою (4.2), є незсуненою обґрунтованою оцінкою Мξ.

2. Оцінка дисперсії та середнього квадратичного відхилення

Для незгрупованої вибірки:

- вибірковою дисперсією називають статистику

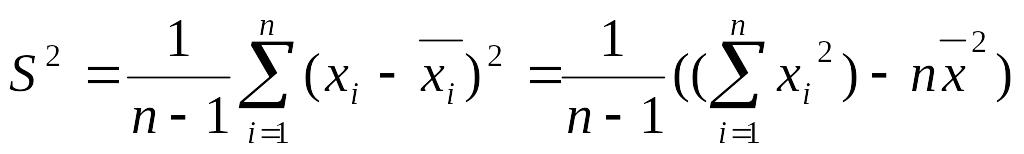; (4.4)

- другим вибірковим центральним моментом називають статистику

(4.5)

Для згрупованої вибірки:

- вибірковою дисперсією називають статистику

; (4.6)

- другим вибірковим центральним моментом називають статистику

(4.7)

де f_i - абсолютна частота,

- середина і-го інтервалу групування,

обчислюється за формулою (4.3).

Вибірковим середнім квадратичним відхиленням називається статистика . Статистики та є статистичними оцінками середнього квадратичного відхилення  випадкової величини .

3. Оцінка медіани

Для незгрупованої вибірки для оцінки med розглядається елемент рангу (див. розділ 1), який називається вибірковою медіаною і позначається med або med х.

Д ля згрупованої вибірки в якості оцінки медіани можна взяти абсцису точки перетину прямої у = 0,5 та графіка функції кумулятивних відносних частот (див. розділ 3). На рисунку 4.1 зображено знаходження медіани для згрупованої вибірки.

Рис.4.1

4) Оцінка моди

Для незгрупованої вибірки за оцінку моди mоd приймається вибірковий елемент, що має найбільшу частоту (див. таблицю частот в розділі 1 ) і позначається mоd.

Для згрупованої вибірки для обчислення моди використовується формула

, (4.8)

де m – номер модального інтервалу групування (тобто того, який містить максимальну кількість вибіркових значень);

h = a_m+1 - a_m; d = | f_m - f_m-1 |; d = | f_m+1 - f_m |.

Зміст формули (4.8) зрозумілий з рисунку 4.2.

Зауважимо, що якщо f_m-1= f_m= f_m+1, то права частина формули (4.8) не визначена. В цьому випадку покладають:

.

Якщо m = 1 або m = k, то у першому випадку покладають f_m-1 = 0, а в другому f_m+1 = 0.

Симетричність вибірки

Якщо випадкова величина  має симетричний розподіл, то слід сподіватися, що вибірка, отримана при дослідженні , також симетрична, тобто “симетрично” розсіяна навколо деякого центру. Ознакою симетричності вибірки є так зване емпіричне правило Юла: симетрична вибірка повинна мати одну моду, яка може бути обчислена за формулою:

(4.9)

Для конкретності наближену рівність розуміємо так: вибіркова мода відрізняється від моди, отриманої за формулою (4.9), не більше ніж на 10% від середнього квадратичного відхилення.

Контрольні питання

1. Що таке статистична оцінка числового параметру випадкової величини?

2. Назвіть відомі вам критерії якості статистичних оцінок.

3. Що таке збіжність за імовірністю?

4. Чому статистичну оцінку ми вважаємо випадковою величиною?

5. Що таке статистика?

6. Які числові параметри можуть прийматися за центр розсіювання випадкової величини?

7. Що таке математичне сподівання випадкової величини? Сформулюйте основні властивості математичного сподівання.

8. Яку статистику приймають за оцінку математичного сподівання?

9. Довести, що величина , обчислена за формулою (4.2), є обґрунтованою незсуненою оцінкою математичного сподівання.

10. Що таке дисперсія? Назвіть основні властивості дисперсії. Що характеризує дисперсія? Як оцінити її за вибіркою?

11. Які статистики наближують середнє квадратичне відхилення?

12. Що таке медіана випадкової величини? Як оцінюється медіана за вибіркою?

13. Що таке мода випадкової величини?

14. Що є ознакою симетричності вибірки?

15. Назвіть відомі вам методи точкового статистичного оцінювання та сформулюйте, в чому саме вони полягають.

Розділ 5. Статистичні оцінки квантилів

Означення. Квантилем рівня  ( 0 <  < 1 ) у випадку неперервних розподілів називається число U_ , яке є найменшим розв’язком рівняння = , де – функція розподілу досліджуваної випадкової величини.

Геометрично це означає, що квантиль рівня  - це найменша з абсцис точок перетину прямої у =  з графіком функції у = (рис.5.1).

Зауваження. При означенні квантиля рівня  слова “найменший розв’язок” необхідні для усунення неоднозначності, яка може виникати при розв’язанні рівняння = . Так, наприклад, графіки функцій у =  та у = можуть мати нескінченну множину спільних точок (тобто рівняння у = має нескінченну кількість розв’язків), в той час як квантиль рівня  визначається однозначно.

Рис. 5.1

Означення. Процентилем рівня  ( 0 <  < 100 ) називається число Q_, яке зв’язане з квантилем співвідношенням: Q_= U_(/100)

Так, наприклад, Q₃₀ = U_0,3; Q₅₀= U_0,5.

Означення. Вибірковий квантиль рівня  - це число U_ , яке має ту властивість, що приблизно -частина вибіркових даних менше за число U_.

Зауваження. Дане означення не визначає вибірковий квантиль однозначно. В літературі можна зустріти різні рекомендації щодо обчислення вибіркових квантилів. Вони несуттєво відрізняються один від одного.

Аналогічну властивість має вибірковий процентиль Q_: менше за Q_ приблизно % вибірки. Дане означення вибіркового квантиля (процентиля) пов’язане з тією властивістю теоретичного квантиля, що для неперервної випадкової величини  квантиль рівня  задовольняє умові: P( <U_ ) = , тобто імовірність того, що випадкова величина  під час експерименту прийме значення менше за число U_, дорівнює . (Наприклад, якщо U_0,3 = -7, то P(  < -7 ) = 0,3.)

Вибіркові квантилі (процентилі) U_ (Q_) є наближенням для теоретичних квантилів U_ (процентилів Q_).

Знаходження вибіркових квантилів (процентилів)

- за незгрупованою вибіркою

Для знаходження вибіркового квантиля (процентиля) рівня  треба спочатку знайти ранг цього квантиля (процентиля). В літературі можна знайти різні вирази з цього приводу. В даній роботі рекомендуються наступні формули:

(для квантилів) (5.1)

(для процентилів) (5.2)

де n – об’єм вибірки.

Наприклад, якщо  = 0,3, n=80, то маємо: .

Якщо ранг вибіркового елемента відомий, то легко знайти відповідний вибірковий елемент (див. розділ 1).

- за згрупованою вибіркою

Будемо знаходити вибіркові квантилі (процентилі) графічним способом. Для цього використаємо графік кумулятивної функції розподілу відносних частот (див. розділ 3). На рівні, що відповідає заданому числу , проведемо пряму у =  до перетину з кумулятою. Найменша з абсцис точок перетину графіків і є шуканий квантиль (див. рис. 5.1).

Зауваження. При проведенні прямої у= необхідно узгодити рівень  з одиницями, в яких проградуйована вісь Оу. Якщо вісь Оу проградуйована в процентах, то  - рівень квантиля – необхідно помножити на 100, а рівень процентиля залишити без змін.

Контрольні питання

1. Що таке квантиль (процентиль) рівня  у випадку неперервних розподілів?

2. Який статистичний та імовірнісний зміст квантиля рівня ?

3. Як зв’язані між собою квантилі і процентилі?

4. Яка частина вибірки лежить між числами і ?

5. Якому методу статистичного точкового оцінювання відповідає графічний спосіб за згрупованою вибіркою?

Розділ 6. Інтервальні оцінки параметрів нормально розподіленої випадкової величини

У попередньому розділі вивчалися точкові оцінки невідомих числових параметрів випадкової величини, тобто оцінки, що задавалися одним числом. Якщо оцінка ^* наближувала параметр , то виникало питання, наскільки точне це наближення, тобто яке відхилення ^* від . Додатнє число , для якого виконується рівність | ^*-  | <  характеризує точність оцінки ^* для параметра . Чим менше число , тим краще оцінка ^* наближує . Але ^* - випадкова величина, та й параметр  невідомий. Тому про нерівність | ^*-  | <  (або її еквівалент ^*-  <  < ^* + ) можна говорити лише з деякою імовірністю. Треба навчитися будувати інтервали, які накриють шукані параметри з потрібною імовірністю.

Означення. Довірчим інтервалом рівня  (0 <  < 1) для невідомого параметра  називають числовий інтервал [z₁, z₂], який накриває невідомий параметр  з імовірністю (1-), тобто

P{   [z₁, z₂] } = 1- (6.1)

Число (1-) називають надійністю, або довірчою імовірністю відповідного інтервалу.

При побудові довірчих інтервалів число  задається заздалегідь. Найчастіше за  береться одне з чисел  = 0,1,  = 0,05 або  = 0,01. Тоді відповідні надійності: 0,9, 0,95 або 0,99. Відзначимо, що інтервальні оцінки невідомих параметрів задаються двома числами z₁, z₂ - початком і кінцем інтервалу, якому повинен належати невідомий параметр з відповідною імовірністю.

Для побудови довірчих інтервалів необхідно знати розподіли величин, які при цьому використовуються.

Означення. Нехай ₁, ₂, ... , _n – незалежні випадкові величини, кожна з яких має розподіл N(0;1). Тоді, за означенням, випадкова величина  = ₁² + ₂² + ... + _n² має розподіл ² з n ступенями свободи (позначення  ~ _n²).

Означення. Нехай ₁ та ₂ - незалежні випадкові величини, причому ₁ ~ N(0;1), а ₂ ~ _n². Тоді, за означенням, випадкова величина має розподіл Стьюдента з n ступенями свободи (позначення  ~ t_n).

Побудова довірчих інтервалів для невідомих математичного сподівання та дисперсії нормально розподіленої випадкової величини базується на теоремі:

Якщо x₁, x₂, …, x_n - вибірка з теоретичним розподілом N(μ; σ), то:

1) статистики та S² - незалежні

(нагадаємо, що ; ) ;

2) ;

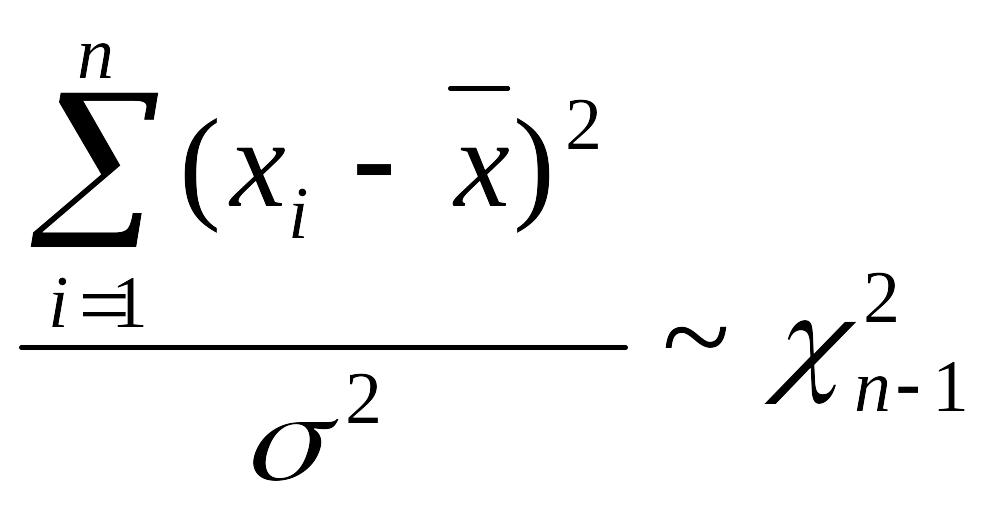3) .

За допомогою цієї теореми легко довести, що за умови нормальності теоретичного розподілу

а) довірчим інтервалом рівня a для математичного сподівання є інтервал

,

де - квантиль рівня 1-/2 розподілу Стьюдента з n-1 ступенями свободи. Квантилі t - розподілу знаходяься за таблицею додатку 3. Для значення об’єму вибірки n, якого немає у таблиці, потрібно знайти наближене проміжне значення квантиля U_n до двох сусідніх і згідно з наступною формулою

,

де n_i < n < n_i+1.

б) довірчим інтервалом рівня a для дисперсії є інтервал

,

де - квантиль рівня 1-/2 розподілу ² з n-1 ступенями свободи. Квантилі ²-розподілу знаходяться за таблицею додатку 4. Якщо значення об’єму вибірки n відсутнє у таблиці, то квантиль U_n визначається як наближене проміжне значення до двох сусідніх і згідно з наступною формулою

,

де n_i < n < n_i+1.

Контрольні питання

1. Що таке інтервальна оцінка? Чим вона відрізняється від точкової?

2. Як розуміти термін “точність оцінки”? Чому про точність інтервальної оцінки можна говорити лише з деякою імовірністю?

3. Що таке довірчий інтервал рівня  для невідомого параметра?

4. Пояснити зміст рівності (6.1).

5. За допомогою якої теореми будуються довірчі інтервали для невідомих математичного сподівання та дисперсії нормально розподіленої випадкової величини?

6. Як знайти вибіркову дисперсію, якщо відомі відповідні довірчі інтервали та об’єм вибірок?

Розділ 7. Перевірка статистичних гіпотез - 1.

Гіпотези відносно імовірностей та середніх значень