МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Київський національний університет технологій та дизайну

Імовірнісні процеси та математична статистика

в легкій промисловості

Статистичний аналіз даних

Методичні вказівки до індивідуальної роботи

КИЇВ КНУТД 2009

Імовірнісні процеси та математична статистика в легкій промисловості. Статистичний аналіз даних. Методичні вказівки до індивідуальної роботи. Для студентів спеціальності „Інформаційні технології проектування” /Упор. С.М. Краснитський, Л.Л. Федотова, О.С. Чайковська. – К.: КНУТД, 2009 – 47 с. Укр. мовою.

Розділ 1. Способи запису та зображення вибіркових даних

Вибірка. Статистичний ряд. “Стеблина з листям”.

Означення. Вибіркою об’єму n будемо називати набір x₁, x₂, …, x_n значень випадкової величини , які отримані при проведенні n незалежних експериментів. Відзначимо, що якщо експерименти відбулися, то вибірка – це набір конкретних чисел. При цьому в багатьох випадках, наприклад, якщо експерименти тільки повинні відбутися, під вибіркою розуміють набір незалежних випадкових величин, кожна з яких має розподіл досліджуваної випадкової величини .

Розглянемо вибірку, отриману при дослідженні міцності нитки пряжі, (в одиницях виміру) яка записана таблицею:

37	13	25	48	1	36
1	22	31	49	61	48
11	23	34	58	25	48
12	24	36	57	31	57

Така форма запису дає мало інформації про особливості вибірки.

Зобразимо вибірку у вигляді так званої таблиці частот, яку інколи називають статистичним рядом.

Таблиця частот Таблиця 1.1

1	11	12	13	22	23	24	25	31	34	36	37	48	49	57	58	61
2	1	1	1	1	1	1	2	2	1	2	1	3	1	2	1	1

У верхньому рядку таблиці записані вибіркові дані, які йдуть по зростанню, у нижньому – частоти, з якими вони зустрічаються у вибірці. Такий запис більш компактний та наочний, хоча багато особливостей і при такому зображенні вибірки залишаються непомітними.

В таблиці 1.2 вибірку зображено ще у одному вигляді, який називається “стеблиною з листям” [3]. Ліворуч від вертикальної риски записана кількість десятків (“стеблина”), праворуч – одиниці наших чисел (“листя”). Зірочка означає, що до кількості десятків дописується по одній цифрі, які йдуть за вертикальною лінією. З таблиці 1.2 видно, що дана вибірка є групою чисел, яка має майже симетричний характер, з концентрацією в середині вибірки та спаданням на кінцях.

“Стеблина з листям” Таблиця 1.2

0*	1	1
1*	1	2	3
2*	2	3	4	5	5
3*	1	2	4	6	6	7
4*	8	8	8	9
5*	7	7	8
6*	1

Доповнимо “стеблину з листям” двома стовпчиками, в першому з яких запишемо кількість елементів у відповідному рядку, а у другому – загальну кількість елементів у цьому та попередніх рядках. Тоді “стеблина з листям” нашої вибірки набуває вигляду:

0*	1	1					2	2
1*	1	2	3				3	5
2*	2	3	4	5	5		5	10
3*	1	2	4	6	6	7	6	16
4*	8	8	8	9			4	20
5*	7	7	8				3	23
6*	1						1	24

З такого рисунку легко знаходити вибіркові елементи за їх рангами (див. “Ранжування вибірки”).

Як видно з таблиці, “стеблина“ вже дає деяку інформацію про вибірку, а “листя“ додає до неї характер розташування окремих елементів вибірки.

Слід зробити деякі зауваження щодо побудови вибірки у вигляді “стеблини з листям“:

1. значення “стеблини“ є зростаючою (або спадною) послідовністю чисел із сталим кроком, до яких додається одна чи декілька зірочок,

2. кількість зірочок відповідає кількості розрядів у числах, що записані як “листя“,

3. для деяких значень “стеблини“ “листя“ може бути відсутнє,

4. замість простої “стеблини з листям“ можна розглядати таку, в якій кожний елемент “стеблини“ має 2 рядки: перший для значень “листя“ 0,1,2,3,4 і другий – для 5,6,7,8,9. Це зручно робити, коли в рядках виявляється забагато чисел.

“Стеблина з листям” стає у нагоді при дослідженні вибірок середнього об’єму (50-200 елементів). При цьому способі запису наочно простежуються такі особливості:

• розділяється вибірка на підгрупи чи являє собою одну групу чисел;

• чи симетричне спадання до кінців усередині підгруп;

• чи є більш-менш популярні області;

• чи великий розкид даних та ін.

Ранжування вибірки. Ранг вибіркових елементів

Процес впорядкування вибірки називається ранжуванням. Найчастіше вибірку впорядковують таким чином, що кожний наступний елемент не менше за попередній. Номер елемента x у впорядкованій вибірці називають рангом елемента x і позначають r(x).

При подальших міркуваннях, якщо x₁, x₂, …, x_n – загальна вибірка, то впорядковану вибірку будемо позначати x₍₁₎, x₍₂₎, …, x_(n).

Нехай t – деяке число; [t] – ціла частина числа t; {t} – дробова частина числа t. Визначимо елемент дробового рангу t за формулою:

x_(t)=x_([t])+{t}( x_([t+1])- x_([t]))

Наприклад, елемент x_(6,3) вибірки (табл.2) дорівнює:

x_(6,3)=x₍₆₎+0,3( x₍₇₎-x₍₆₎)=22+0,3(23-22)=22,3.

Медіаною вибірки об’єму n будемо називати вибірковий елемент, ранг якого дорівнює . Медіана позначається med або medx. За означенням

Наприклад, медіана вибірки (табл.1) дорівнює:

.

Нижнім квартилем вибірки називається вибірковий елемент С₁, ранг якого розраховується за формулою: .

Верхнім квартилем вибірки називається вибірковий елемент С₂, ранг якого розраховується за формулою: .

Квартилі разом із медіаною ділять впорядковану вибірку на чотири однакові за об’ємом частини.

Знайдемо квартилі розглядуваної вибірки (табл.2):

;

;

;

.

“Ящик з вусами”

“Ящик з вусами” [3] – це ще одна з форм (графічна) зображення вибіркових даних. Побудова “ящика з вусами” стане зрозумілою з наступного рисунку, де : x_min = min{x₁, x₂, …, x_n} = x_[1];

x_max = max{x₁, x₂, …, x_n}= x_[n]

Інколи буває так, що окремі вибіркові значення розташовані далеко від основної групи даних. На практиці це може бути, наприклад, обумовлено грубими похибками при фіксації результатів експеримента. Було б зручно мати правило відділення таких значень. З цією метою вводяться [3] спеціальні числові характеристики вибірки, що мають назву “бар’єри“. Останні визначаються за вибіркою за наступною схемою:

1. позначимо С₂ – С₁ = С,

2. “внутрішні бар’єри“ визначимо за межами інтервалу [С₁,С₂] на відстані 1,5·С від С₁ і С₂,

3. “зовнішні бар’єри“ визначимо за межами інтервалу [С₁,С₂] на відстані 2·С від С₁ і С₂,

4. значення за “зовнішніми бар’єрами“ будемо називати “віддаленими“,

5. значення між “внутрішніми“ і “зовнішніми бар’єрами“ будемо називати “зовнішніми“,

6. значення, що знаходяться ближче до “внутрішніх бар’єрів“ зсередини, назвемо “прилеглими“.

Згідно з [3], відсутність серед вибіркових значень “віддалених“ або “зовнішніх“ вказує на певну “компактність“ розташування даних. Навпаки, наявність вказаних значень вказує на помітну величину розкиду даних.

Для побудови “ящика з вусами“ із врахуванням “внутрішніх“ і “зовнішніх бар’єрів“ будемо додержуватись наступних правил:

1. “вуса“ слід рисувати пунктиром і закінчувати рискою, що відповідає “прилеглим“ значенням,

2. “зовнішні“ і “віддалені“ значення слід наносити окремо.

Зауважимо, що при побудові “ящика з вусами“ на вертикальній лінії треба ввести масштаб і при нанесенні на ній відповідних значень суворо його додержуватись. Що стосується “віддалених“, “зовнішних“ і “прилеглих“ значень, то їх участь у наступному статистичному аналізі вибірки визначається як конкретним змістом значень вибірки, так і дослідником, який буде обробляти ці дані.

Контрольні питання

1. Що таке вибірка?

2. Що називається статистичним рядом?

3. Як будувати “стеблину з листям”? Про що можна дізнатися з такого зображення вибіркових даних?

4. Що таке ранг вибіркового елемента? Як знаходити елементи дробового рангу?

5. Прокоментувати графічне зображення вибіркових даних - “ящик з вусами”.

Розділ 2. Групування вибірки. Полігон і гістограма

Для полегшення аналізу вибірок великого об’єму використовується так зване групування вибірки з наступною побудовою полігонів і гістограм.

Процедура групування полягає в заміні індивідуальних вибіркових значень x₁, x₂, …, x_n деякою сукупністю числових інтервалів (інтервалів групування) [ , ], [ , ], …, [ , ], k>1 та вказівкою, скільки вибіркових значень належить кожному з цих інтервалів. При цьому об’єднання всіх зазначених інтервалів повинно містити в собі всі вибіркові значення x₁, x₂, …, x_n.

Сукупність інтервалів групування і відповідних кількостей вибіркових значень називається згрупованою вибіркою.

Частіше за все використовують інтервали групування однакової ширини. Існують різні методики їх побудови. В даній роботі для групування вибірки пропонується наступна послідовність дій.

1) Визначається наближена кількість інтервалів групування за формулою:

, (2.1)

де n – об’єм вибірки; - ціла частина числа .

2) Визначається довжина інтервалу групування за правилом:

, (2.2)

де x_max , x_min – відповідно максимальне та мінімальне вибіркові значення. Відзначимо, що для спрощення побудови число h як правило заокруглюють.

3) Визначаються числа a₁, a₂, ..., a_k+1 (і тим самим – інтервали групування) за формулою:

,

де i змінюється від 1 до k, а число k визначається з нерівності: . Числа a_i , a_i+1 називаються нижньою та верхньою границями i-го інтервалу групування. За нижню границю першого інтервалу групування можна взяти довільне число, але так, щоб в інтервалі [a₁,a₂] міcтилось принаймі одне вибіркове значення. Визначимо a₁ , наприклад, наступним чином:

. (2.3)

Означення. Абсолютною частотою i-го інтервалу групування називається кількість вибіркових елементів у даному інтервалі (позначається f_i).

Зауваження. Кінець і-го і початок (і+1)-го інтервалів групування збігаються. Тому, якщо вибіркові значення потрапляють на цей “стик”, то половину із них належить віднести до і-го інтервалу, а іншу половину – до (і+1)-го, тобто абсолютна частота і-го інтервалу може бути дробовим числом.

Означення. Гістограмою (від грецького “гістос” - стовп) абсолютних частот називається фігура, утворена із прямокутників, побудованих на інтервалах групування як на основах, а висота кожного прямокутника дорівнює абсолютній частоті відповідного інтервалу групування.

Означення. Полігоном (від грецьких “полі” – багато, “гон” - кут) абсолютних частот називається ламана, утворена послідовним сполученням на площині точок з координатами , де - середина i-го інтервалу групування, тобто , f_i - абсолютна частота i-го інтервалу групування.

Слід зазначити, що наведена вище методика визначення кількості інтервалів дозволяє одержати для полігону умовно плавну криву, яка дає приблизне уявлення про закон розподілу випадкової величини, що представлена вибіркою об'єму n. При збільшенні кількості інтервалів без збільшення n ця крива може мати гострі вершини і провали, що візуально заважає представити наближено закон розподілу.

Розглянемо побудову гістограми та полігону абсолютних частот на прикладі вибірки, поданої в вигляді таблиці 1.1 (див. розділ 1). У цій вибірці 24 елементи, тому

;

.

Знайдемо границі інтервалів. За формулою (2.3) маємо:

;

далі отримаємо:

;

; і т. д.

Для побудови полігонів та гістограм зручно попередньо заповнити таблицю “групування - частоти”. Так для нашого прикладу відповідна таблиця має вигляд:

Таблиця “групування - частоти” Таблиця 2.1

№	границі	інтервалів	середні точки	абсолютні частоти
i	ai	ai+1		fi
1	0,5	10,5	5,5	2
2	10,5	20,5	15,5	3
3	20,5	30,5	25,5	5
4	30,5	40,5	35,5	6
5	40,5	50,5	45,5	4
6	50,5	60,5	55,5	3
7	60,5	70,5	65,5	1

Гістограма та полігон абсолютних частот даної вибірки:

За побудованою гістограмою (полігоном) можна зробити наступні висновки:

а) вибіркові значення лежать в інтервалі від 0,5 до 70,5;

б) найбільш часто зустрічаються значення, що належать інтервалу від 30,5 до 40,5; найбільш рідко – в інтервалі від 60,5 до 70,5;

в) проглядається певна симетричність відносно центральних інтервалів.

При аналізі вибірок різного об'єму доцільно використовувати відносну частоту , де п – об'єм вибірки, f_i – абсолютна частота на і-му інтервалі. Відносну частоту і-го інтервалу можна інтерпретувати як ймовірність попадання значення випадкової величини в і-тий інтервал. Якщо ж групуванння елементів вибірки виконується з різною довжиною інтервалів групування, то доцільно використовувати зведені частоти , де h – довжина і-го інтервалу групування, f_i – абсолютна частота на і-му інтервалі.

Побудуємо гістограму у зведених частотах. Тоді площа кожного прямокутника дорівнює абсолютній частоті відповідного інтервалу. При переході до іншого поділу на групи виявляється дуже легким обчислення частот нових інтервалів. Ці частоти будуть наближено дорівнювати сумі площ прямокутників, які утворилися (або вже існували) при переході до нових інтервалів групувань.

Контрольні питання

1. Що розуміють під групуванням вибірки?

2. Що таке абсолютна частота інтервалу групування?

3. Що називається полігоном, гістограмою?

4. Відносні та приведені частоти. Їх гістограми і полігони.

Розділ 3. Вибіркові аналоги функції та щільності розподілу

Нехай вибірка x₁, x₂, … , x_n - це незалежні спостереження за випадковою величиною  з функцією розподілу .

Нагадаємо, що функцією розподілу випадкової величини  називається функція , x(- ; + ), яка визначається рівністю:

= P( <x ).

Якщо функція розподілу може бути представлена в вигляді:

де f(x) – деяка невід’ємна функція, то випадкова величина  називається абсолютно неперервною, а для функції f(x) використовується назва щільності розподілу.

Функція розподілу випадкової величини, значення (інакше, реалізації) якої утворюють вибірку, називається теоретичною функцією розподілу. Аналогічно, щільність цієї величини називають теоретичною щільністю розподілу.

Наше завдання полягає в тому, щоб оцінити невідомі теоретичну функцію розподілу та теоретичну щільність розподілу , f(x). Іншими словами, треба за вибіркою побудувати деякі функції, які будуть наближувати та f(x) при великих об’ємах вибірки n. Такими функціями є емпірична функція розподілу , кумулятивна функція розподілу та гістограма щільностей f_n^*(x).

Емпірична функція розподілу F_n(x)

Означення. Емпіричною функцією розподілу називається функція, яка задається формулою , де К_n(x) – число вибіркових значень х_і таких, що х_і<x, n – об’єм вибірки.

Наведемо приклад розрахунку значення F_n(x) для вибірки (-4, -1, 1, 2, 7). Оскільки вибірка вже є впорядкованою (якщо це не так, то її потрібно перш за все впорядкувати), знайдемо значення K_n , наприклад, для х = 0,3. Маємо K_n(0,3) = 2; отже F_n(0,3) = 2/5.

Представимо вибірку у вигляді таблиці частот:

x(1)	x(2)	…	x(m)
n1	n2	…	nm

де x₍₁₎ < x₍₂₎ < … < x_(m);

n_i – кількість повторень елемента x_(і) у вибірці; n₁+n₂+…+n_m= n. Тоді побудова графіка функції стає зрозумілою з рисунку 3.1.

Для будь-якого фіксованого х: при n → ∞, тобто прямує до за імовірністю. Це означає, що функція буде обґрунтованою оцінкою для теоретичної функції розподілу .

Рис. 3.1

Попередня оцінка функції будувалась за незгрупованою вибіркою. Розглянемо ще одну оцінку для .

Кумулятивна функція розподілу F_n^*(x)

Для згрупованої вибірки за оцінку функції розподілу часто вибирають так звану кумулятивну функцію розподілу , або скорочено - кумуляту (від латинського “кумуляція” - накопичення).

Нехай вибірка, що розглядається у розділі 1, згрупована за методикою розділу 2. Для побудови кумулятивної функції розподілу спочатку необхідно знайти абсолютні і відносні кумулятивні частоти. Ці частоти визначаються за формулами:

(3.1)

і=1, 2, ... , k, (3.2)

де f_i – абсолютна частота i-го інтервалу групування [a_i, a_i+1]; k – число інтервалів групування. Тоді за означенням:

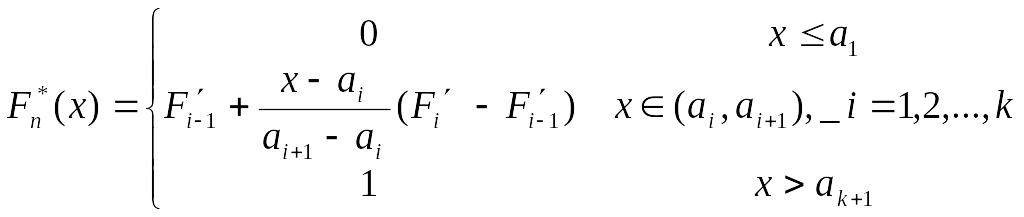_, (3.3)

де а₁, а₂, … , а_k+1 – границі інтервалів групування.

Іншими словами, для < x < одержуємо, з’єднуючи відрізками прямих точки площини з координатами ( , ), i=0, 1, 2,…, k. Графік кумулятивної функції розподілу наведено на рис. 3.2.

Рис. 3.2

Поряд з кумулятивною функцією розглядають кумулятивну функцію абсолютних частот, яку можна одержати із рис. 3.2, замінивши відносні кумулятивні частоти на абсолютні кумулятивні частоти та проградуювавши вісь Оу не від 0 до 1, а від 0 до n.

Гістограма щільностей f_n^*(x)

Поряд з абсолютними і відносними частотами розглядаються так звані вибіркові щільності, які визначаються наступним чином:

,

де – абсолютна частота і-го інтервала;

n – об’єм вибірки;

h – довжина інтервалів групування.

Аналітично гістограма щільностей задається наступною формулою:

(3.4)

Гістограма щільностей є оцінкою невідомої щільності розподілу випадкової величини .

З формул (3.3), (3.4) неважко переконатися, що для x  a_i, i = 1,2,…,k:

а також .

Звідси та з попередніх викладок маємо наступні рівності:

, (3.5)

які дозволяють для великих n наближено знаходити імовірність попадання випадкової величини  в довільний інтервал (, ). Аналогічно, імовірність із співвідношення (3.5) наближено дорівнює також .

Використовуючи функції F_n(x), та оцінити ймовірність попадання випадкової величини в деякий інтервал (α,β) можна трьома способами.

Перший спосіб - за емпіричною функцією розподілу F_n(x). Для цього треба знайти за графіком емпіричної функції значення F_n(α), F_n(β) і знайти різницю F_n(β) - F_n(α). Вона і буде шуканою оцінкою.

Другий спосіб – за кумулятивною функцією розподілу . Спочатку треба обчислити абсолютні F_i і відносні кумулятивні частоти згідно з формулами (3.1) і (3.2). Далі побудувати графік кумулятивної функції розподілу за даними для згрупованої вибірки. Знайти за графіком , і обчислити різницю - (шукана оцінка).

Третій спосіб – за гістограмою щільностей. Для цього треба спочатку обчислити значення для згрупованої вибірки і побудувати гістограму щільностей. В точках α і β на осі х провести перпендикуляри до перетину з горизонтальними лініями гістограми щільностей і обчислити площу тієї частини гістограми щільностей, яка обмежена цими перпендикулярами – це і буде оцінкою ймовірності попадання випадкової величини в інтервал (α,β).

Контрольні питання

1. Що таке функція розподілу випадкової величини? Сформулюйте її основні властивості.

2. Що таке теоретична функція розподілу?

3. Як за вибіркою оцінити невідому теоретичну функцію розподілу?

4. Що таке щільність розподілу випадкової величини? Сформулюйте її властивості.

5. Що таке теоретична щільність розподілу?

6. Як за вибіркою оцінити невідому щільність розподілу неперервної випадкової величини?

7. Як за вибіркою даної випадкової величини знайти наближено величину ?

8. На якому теоретичному результаті базується можливість оцінки теоретичної функції розподілу емпіричною функцією розподілу?

Розділ 4. Точкові статистичні оцінки основних числових параметрів випадкової величини

При дослідженні випадкових величин часто виникає потреба охарактеризувати випадкову величину за допомогою декількох чисел. Найбільш важливими є числа, що задають:

• центр, навколо якого розсіюються значення випадкової величини;

• відхилення (середнє) випадкової величини від центру розсіювання.

За центр значень випадкової величини , який є характеристикою її розміщення, найчастіше приймають одне з наступних чисел:

• математичне сподівання випадкової величини М;

• медіану випадкової величини med ;

• моду випадкової величини mоd .

Нагадаємо, що математичне сподівання випадкової величини  - це число, яке обчислюється за однією з формул:

а) - для абсолютно неперервних випадкових величин із щільністю розподілу .

б) - для дискретних випадкових величин, які приймають значення x_i з імовірністю p_i (і=1, 2, ...).

Медіаною (med ) неперервної випадкової величини  будемо називати найменше з чисел х, для яких Р( <x ) = 0,5. Це означає, що число med  ділить числову вісь на інтервали, в які випадкова величина  попадає з однаковою імовірністю 0,5.

Під модою випадкової величини  будемо розуміти число mоd , яке є:

• точкою максимуму щільності розподілу, якщо  - абсолютно неперервна випадкова величина;

• значенням, яке випадкова величина  приймає з найбільшою імовірністю, якщо  - дискретна випадкова величина.

Зрозуміло, що випадкова величина  може мати декілька мод і що числа М, med та mоd не обов’язково рівні між собою, але якщо вони співпадають, то будемо казати, що випадкова величина має симетричний відносно центру (або просто симетричний) розподіл.

Основними параметрами, які характеризують міру відхилення випадкової величини  від центру є дисперсія D та середнє квадратичне відхилення _ξ.

Нагадаємо, що D = М(-М )², а _ξ = .

Нехай x₁, x₂, … , x_n - вибірка, отримана при дослідженні випадкової величини , основні числові параметри якої відомі. Потрібно по результатам наших спостережень, тобто по вибірці x₁, x₂, … , x_n , знайти числа, які б були наближеннями невідомих параметрів досліджуваної випадкової величини.

Під точковою статистичною оцінкою невідомого числового параметра  будемо розуміти функцію _n^*= g( x₁, x₂, … , x_n ) вибіркових значень x₁, x₂, … , x_n , яка дає наближення значення параметра , тобто  ~ g( x₁, x₂, … , x_n ) (надалі слово “точкова” часто буде опускатися). Таким чином, для знаходження оцінки числового параметра потрібно підібрати функцію g( x₁, x₂, … , x_n ), яку називають статистикою, значення якої на конкретній вибірці давало б наближення невідомого числового параметра.

Оскільки до початку експериментів вибіркові значення вважаються невідомими і всі вони можуть вважатися випадковими величинами x₁, x₂, …, x_n , то функцію _n^* = g( x₁, x₂, … , x_n ) можна розглядати як деяку випадкову величину _n^*.

Зрозуміло, що для кожного числового параметра треба підібрати свою статистику, більш того, для оцінки одного і того ж параметра можна підібрати різні статистичні оцінки.