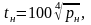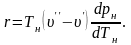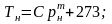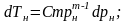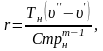Лабораторна робота № 4 експериментально-теоретичне дослідження фазових переходів ''рідина – насичена пара''
Мета роботи: оволодіння методикою дослідного вивчення фазових переходів, набуття практичних навичок в користуванні приладами, що застосовуються для експерименту.
Робота проводиться для закріплення теоретичних знань з розділу ''Реальні гази''.
За даними проведеного експерименту необхідно встановити залежність між тиском і температурою насиченої пари рідини, яку ми досліджуємо, та підібрати емпіричну формулу, яка б відображала цю залежність з допустимою похибкою. Також необхідно встановити залежність між теплотою пароутворення і температурою насичення.
До виконання лабораторної роботи слід вивчити розділи курсу ''Реальні гази'', ''Пари'' [3,4].
Загальні відомості
Удосконалення парових теплосилових установок диктує необхідність дослідження поведінки реальних речовин в широкому діапазоні тисків і температур.
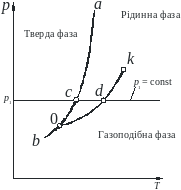
З рис.4.1 видно, що теплота пароутворення (теплота процесу b c) при досягненні критичних параметрів зменшується до нуля. Ізотерма, що проходить через критичну точку, має перетин у точці k.
Таким чином, тут виконуються умови:
|
(4.1) |
На діаграмі p-T виділено точки: 0 – потрійна точка; с – точка переходу ''тверде тіло - рідина'' (точка плавлення або твердіння); d – точка кипіння (конденсації).
|
|
Рис.4.1. p-υ і p-T - діаграми стану реальної речовини
При аналізі фазових рівноваг і процесів фазових переходів широко використовується так зване правило фаз Гіббса:
|
(4.2) |
де
 – число незалежних змінних, що визначають
стан системи, яка знаходиться у рівновазі
(ці незалежні змінні часто називають
ступенями вільності системи); n
– число компонентів системи; m
– число фаз в системі.
– число незалежних змінних, що визначають
стан системи, яка знаходиться у рівновазі
(ці незалежні змінні часто називають
ступенями вільності системи); n
– число компонентів системи; m
– число фаз в системі.
Для чистої речовини (n=1) правило фаз має вигляд
|
(4.3) |
Звідки для чистої речовини в однофазній системі (m=1) число ступенів вільності дорівнює двом. Такими незалежними змінними часто є р і Т, які однозначно визначають інші інтенсивні параметри системи.
Якщо
число фаз для попереднього випадку
дорівнює двом, система має один ступінь
вільності, а саме: тільки температура
(або тільки тиск) фазового переходу
визначає собою всі інші інтенсивні
термодинамічні величини кожної з фаз.
В даному випадку існує залежність
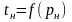 ,
конкретний вигляд якої визначається
природою речовини. Фазовий перехід в
р-Т-діаграмі
відображається точкою.
,
конкретний вигляд якої визначається
природою речовини. Фазовий перехід в
р-Т-діаграмі
відображається точкою.
Повернемося до процесу пароутворення ''b–c''. Теплота пароутворення r за першим законом термодинаміки може бути представлена як сума двох частин – роботи розширення і роботи дисгрегації (перетворення рідини на пару).
Позначивши роботу дисгрегації ρ, а роботу розширення – ψ, отримуємо
|
(4.4) |
|
(4.5) |
Перший закон термодинаміки для процесу пароутворення можна записати у вигляді
|
(4.6) |
Для
ідеальних газів робота дисгрегації
дорівнює нулю, а в насичених парах вона
незначна. Так, наприклад, для водяної
пари відношення
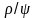 наведено
у табл.4.1.
наведено
у табл.4.1.
Таблиця 4.1. Відношення
|
0,1 |
2,0 |
5,0 |
10,0 |
20,0 |
|
12,4 |
9,46 |
7,6 |
7,0 |
6,61 |
Теплота
пароутворення r
і внутрішня теплота пароутворення
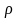 зменшуються із підвищенням тиску (як
наслідок, і температури) і стають рівними
нулю за критичних параметрів.
зменшуються із підвищенням тиску (як
наслідок, і температури) і стають рівними
нулю за критичних параметрів.
Теплота
пароутворення r,
приріст питомого об’єму в процесі
пароутворення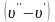 ,
тиск
і температура насичення Tн
пов’язані між собою залежністю, яка в
термодинаміці має назву рівняння
Клапейрона-Клаузіуса і виводиться у
теоретичному курсу:
,
тиск
і температура насичення Tн
пов’язані між собою залежністю, яка в
термодинаміці має назву рівняння
Клапейрона-Клаузіуса і виводиться у
теоретичному курсу:
|
(4.7) |
Рівняння (4.7) дозволяє обчислити теплоту фазових переходів, якщо відомі надійні залежності
|
(4.8) |
Точне теоретичне виведення залежностей (4.8) на сьогодні ще не отримано. Тому в обчислювальній практиці використовують експериментальні дані або емпіричні формули, достатньо точні в указаному інтервалі незалежної змінної. Для водяної пари існує багато емпіричних формул типу (4.8). Однією з них є формула Руша (система одиниць МКГСС)
|
(4.9) |
де
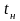 виражається
в оС;
–
в ат. Для водяної пари формула справедлива
до
виражається
в оС;
–
в ат. Для водяної пари формула справедлива
до
 Відомі
також інші залежності, наприклад формула,
запропонована А.Б. Болгарським та ін.
Відомі
також інші залежності, наприклад формула,
запропонована А.Б. Болгарським та ін.
Для експериментального вимірювання тиску пари над рідиною і твердими речовинами розроблена велика кількість методик [1]. В нашому випадку для побудови кривої насичення можуть бути застосовані статичний метод точок кипіння.
В даній роботі залежність (4.8) встановлюється експериментальним шляхом, а теплота пароутворення – наступним чином.
Рівняння Клапейрона–Клаузіуса можна подати у вигляді
|
(4.10) |
Величину
похідної можна отримати графічно,
використовуючи графік залежності
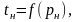 або безпосереднім диференціюванням
експериментальної залежності типу
або безпосереднім диференціюванням
експериментальної залежності типу

Тоді
|
(4.11) |
|
(4.12) |
|
(4.13) |
Враховуючи (4.13), теплота пароутворення r може бути обчислена за виразом
|
(4.14) |
де
m,C
– сталі, визначені експериментально;
– абсолютний тиск насичення, Па;
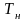 – абсолютна температура, К;
– різниця питомих об’ємів сухої
насиченої пари і води, що кипить при
тиску
,
м3/кг
(визначається за допомогою таблиць).
– абсолютна температура, К;
– різниця питомих об’ємів сухої
насиченої пари і води, що кипить при
тиску
,
м3/кг
(визначається за допомогою таблиць).

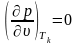 і
і
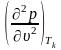


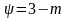 .
.
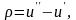

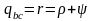 .
.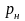 ,
МПа
,
МПа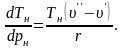
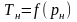 і
і