Плоские статически определимые фермы

Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирами.

В фермах стержни соединены в узлах или на болтах, или на сварке, т.е. жестко. Однако, как показывают сравнительные расчеты при действии на ферму узловой нагрузки усилия в ферме с шарнирными узлами и жесткими узлами мало отличаются. Например, усилия в идеальной ферме с шарнирами на 10% больше усилий в болтовых фермах. Будем рассматривать только фермы с идеальными шарнирами. В таких фермах при узловом действии нагрузки в стержнях будут возникать только сжимающие или растягивающие усилия.

Классификация ферм

1. По назначению:

а) фермы пролетных строений мостов; б) крановые фермы; в) фермы каркасов промышленных зданий; г) фермы башенного типа.

2. По характеру опорных закреплений:

а) балочные, б) арочные, в) консольные, г) неразрезные.

3. По очертанию опорных поясов:

а) фермы с параллельными поясами, б) фермы с полигональными поясами.

4. По системе решетки:

а) фермы с треугольной решеткой, б) шпренгельные фермы, в) фермы с раскосной решеткой, г) многорешетчатые фермы, д) фермы с ромбической решеткой.

5. По методу расчета:

а) статически определимые, б) статически неопределимые.

До определения усилий в стержнях ферм необходимо вычислить общее число неизвестных n: n = C + C₀, где С – число стержней фермы, С₀ – число опорных стержней. Для каждого узла фермы составляются два уравнения равновесия: Σx= 0 и Σy = 0, следовательно, общее число уравнений равно 2Y, где Y – число узлов. Таким образом, для статически определимой фермы необходимо выполнение условия:

2Y = С + С₀ или W = 2Y – С – С₀. (1)

Формула (1) дает возможность провести кинематический анализ. В структурном анализе надо доказать, что диски фермы соединены между собой по закону жесткого треугольника.

Аналитические методы расчета ферм

Для расчета простых ферм применяются различные методы. Рассмотрим их на конкретном примере (рис.1).

Метод вырезания узлов.

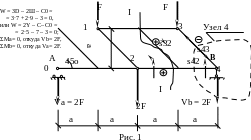Вырежем узел 4 (рис. 1) и рассмотрим его равновесие (рис 2):

Σy = s₄₃cos45^o + 2F = 0, откудаs₄₃ = –2F/cos45^o,

знак (–) показывает, что стержень 3–4 сжат, следовательно, на рис. 2 необходимо изменить направление усилия s₄₃. Затемсоставляем

Σx = –s₄₂ + s₄₃cos45^o = 0, тогдаs₄₂ = s₄₃cos45^o = 2F.

В дальнейшем следует применить следующий порядок вырезания узлов: узел 3, узелА, узел 1.

Если в узле сходятся три стержня, из которых два направлены одинаково и нет нагрузки, то усилие в отдельно направленном стержне равно нулю (рис. 3).

При вырезании узлов необходимо, чтобы число неизвестных усилий в нем не превышало двух.

Метод моментных точек

Проведем сечение I–I и отбросим левую часть фермы (рис. 1). Для оставшейся части точка 3 будет моментной:

ΣM₃ = V_ba – s₄₂ a= 0, тогдаs₄₂ = V_b = 2F.

Метод полного сечения (способ проекций)

Рассмотрим сечение I–I. Отбросим левую часть, а для оставшейся части составим условие:

Σy = –s₃₂sin45^o – F + V_b = 0, откудаs₃₂ = (–F + V_b)/sin45^o = F/sin45^o.

Метод двух или нескольких сечений

Делается два или несколько сечений, составляются уравнения статики и совместно решаются.

Метод замкнутых сечений

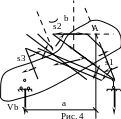
Делается замкнутый разрез, который пересекает некоторые стер-жни два раза. Усилия дважды пересеченных стержней в уравнения статики не войдут (рис. 4). Например, для замкнутого сечения, показанного на рис. 4, имеем:

ΣM_А= s₃b + V_ba= 0,

тогдаs₃ = V_ba/b.

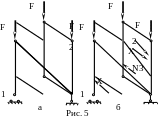
Метод замены стержней

Путем замены стержней ферма превращается в простую, которая кладется в основу расчета. Например, на ферме, показанной на рис. 5, а, убираем стержень 1–2, а его влияние заменяем фиктивной внешней силой Х и ставим дополнительный стержень, усилие в котором обозначим через N₃. Усилие Х (рис. 5, б) определяется из условия, что N₃= 0. Положим Х = 1 и находим 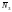, а усилие в фиктивном стержне только от внешней нагрузки обозначим через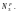 В этом случае запишем:

тогда после чего определяем усилия в остальных стержнях.

Л е к ц и я 5

Основные теоремы об упругих линейно-деформируемых системах. Принцип возможных перемещений. Теорема о взаимности работ (теорема Бетти). Теорема о взаимности перемещений (теорема Максвелла).