
Метод наименьших квадратов (расчёт коэффициентов)
На практике линия регрессии чаще всего
ищется в виде линейной функции
![]() (линейная
регрессия), наилучшим
образом приближающей искомую кривую.
Делается это с помощью метода
наименьших квадратов,
когда минимизируется сумма квадратов
отклонений реально наблюдаемых
от
их оценок
(линейная
регрессия), наилучшим
образом приближающей искомую кривую.
Делается это с помощью метода
наименьших квадратов,
когда минимизируется сумма квадратов
отклонений реально наблюдаемых
от
их оценок
![]() (имеются
в виду оценки с помощью прямой линии,
претендующей на то, чтобы представлять
искомую регрессионную зависимость):
(имеются
в виду оценки с помощью прямой линии,
претендующей на то, чтобы представлять
искомую регрессионную зависимость):

(M — объём выборки). Этот подход основан
на том известном факте, что фигурирующая
в приведённом выражении сумма принимает
минимальное значение именно для того
случая, когда
![]() .
.
Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

Условие минимума функции невязки:

Полученная система является системой
![]() линейных
уравнений с
неизвестными
линейных
уравнений с
неизвестными
![]()
Если представить свободные члены левой части уравнений матрицей

а коэффициенты при неизвестных в правой части матрицей

то получаем матричное уравнение:
![]() ,
которое легко решается методом
Гаусса. Полученная матрица
будет матрицей, содержащей коэффициенты
уравнения линии регрессии:
,
которое легко решается методом
Гаусса. Полученная матрица
будет матрицей, содержащей коэффициенты
уравнения линии регрессии:

Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса-Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.
2 Описание применяемой программы
Для нахождения поставленной цели будет использовать Инструментальную среду Delphi. Delphi - императивный, структурированный, объектно-ориентированный язык программирования, диалект Object Pascal. Начиная со среды разработки Delphi 7.0, в официальных документах Borland стала использовать название Delphi для обозначения языка Object Pascal. Начиная с 2007 года уже язык Delphi (производный от Object Pascal) начал жить своей самостоятельной жизнью и претерпевал различные изменения, связанные с современными тенденциями (например, с развитием платформы .NET) развития языков программирования: появились class helpers, перегрузки операторов и другое. Изначально среда разработки была предназначена исключительно для разработки приложений Microsoft Windows, затем был реализован также для платформ Linux (как Kylix), однако после выпуска в 2002 году Kylix 3 его разработка была прекращена, и, вскоре после этого, было объявлено о поддержке Microsoft .NET.
2.1 Описание интерфейса программы
Перейдём к описанию Интерфейса программы. На рисунке 1 показаны все использующиеся в интерфейсе программы детали: 3 кнопки, таблица, график и 4 поля ввода, поля ввода были описаны ранее, в таблице открываются данные, в поле графика появляется график полинома, и оставшиеся кнопки служат для загрузки Microsoft Office Excel и вывода коэффициентов.

Рисунок 1-Интерфейс программы.
Описание диалоговых окон
При запуске программы появляется следующие окно рисунок 2. На нём представлены все необходимые кнопки и поля для ввода и поле для рисование графика так же поле, где будет отображаться таблица с исходными данными.
Рисунок 2-Общий вид программы
При нажатии на кнопку "Открыть файл" открывается диалоговое окно, в котором нужно выбрать файл с экспериментальными данными рисунок 3.

Рисунок 3- Окно открытия файла данных
На рисунке 4 представлены все поля ввода и вывода данных. Поля N,A0,A1,A2 существуют для ввода и вывода данных, так в поле N мы вводим степень полинома, а в полях A0,A1,A2 выводятся эти самые коэффициенты.
Рисунок 4- Поля ввода и вывода
2.2 Исходные данные программы
Исходными данными к этой программе служит таблица экспериментальных данных представленная на рисунке 5.
 Рисунок
5-Таблица исходных данных
Рисунок
5-Таблица исходных данных
3 Результат решения и тестирования
Проверка и тестирование программы при всех допустимых значениях.
При n=1 результат решения представлен на рисунке 6.

Рисунок 6-Коэффициенты полинома 1 степени.
При n=2 результат решения представлен на рисунке 7
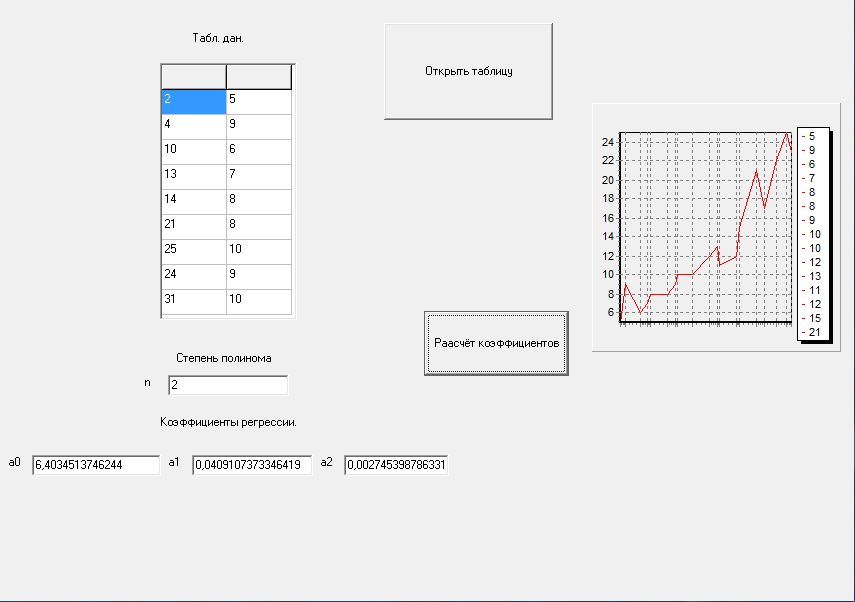
Рисунок 7- Коэффициенты полинома 2 степени.
Оба результата совпадают с расчетами, проведёнными в Microsoft Office Excel рисунок 9 (Приложени 3)
