Доказательство утверждения 1.4.2.

Из (1.4.4) следует, что

(1.4.8)

Имеем

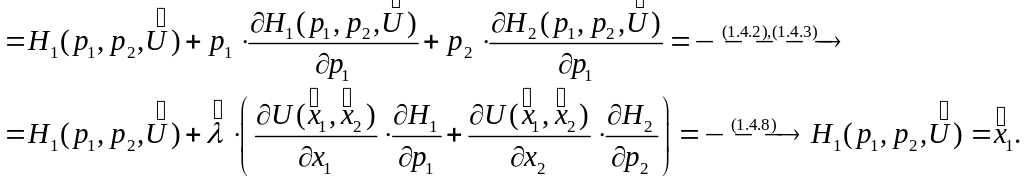
Равенство (1.4.7) получается аналогично.

Утверждение 1.4.2 доказано.

Утверждение 1.4.2 позволяет оценить новый расхода, который при относительно малом изменении цены (при этом новую задачу на условный минимум

решать не следует) имеет вид:

откуда следует, что

т.е.

что важно с теоретической и практической точек зрения.

Утверждения 1.4.1 и 1.4.2. при имеют вид

1.5 Взаимосвязь между решением задач максимизации функции полезности и минимизации расходов. Вывод уравнений Слуцкого. Уравнения Слуцкого в эластичностях.

Задача максимизации функции полезности имеет вид:	Задача минимизации расходов:
(1.5.1)	(1.5.3)
(1.5.2)	(1.5.4)
Вектор - её максимальное решение, (см. Рис. 1.6)	Вектор - её минимальное решение,

Положим в (1.5.2) тогда, очевидно,

(1.5.5)
(1.5.6)

Используя теорему о частных производных сложной функции, будем иметь

(1.5.7)
	(здесь

Подставив в (1.5.5) (лемма Шепарда – см. параграф 1.4) получим уравнение (точнее уравнения) Слуцкого.

(1.5.8)

(в общем случае

В уравнении (1.5.8) вместо фигурирует ибо они равны (см. (1.5.5), (1.5.6)).

По лемме Шепарда (см. параграф 1.4)

(в общем случае

откуда следует, что

В связи с тем, что

имеем

т.е.

(1.5.9)

(в общем случае

Выражение (1.5.9) – это вторая версия уравнений Слуцкого.

Матрица из вторых частных производных

называется матрицей Слуцкого.

Из математического анализа известно, что для выпуклости (вверх) функции расходов, необходимо и достаточно, чтобы матрица Слуцкого была отрицательно полуопределённой, что эквивалентно тому, что квадратичная форма, соответствующая матрице Слуцкого, была отрицательно полуопределённой. Поскольку функция расходов выпукла вверх по переменным и (см. параграф 1.3), постольку матрица Слуцкого отрицательно полуопределена, откуда следует, что все элементы её главной диагонали неположительны

откуда следует, что

т.е. с точки зрения функций спроса по Хиксу все продукты обыкновенные и, продуктов Гиффена у этих функций не бывает.

Уравнение Слуцкого

после деления на и умножения на перепишется так

Преобразовав последнее слагаемое

получим следующее уравнение

(1.5.10)

где - перекрёстная эластичность спроса (по Маршаллу) на й продукт по цене ого продукта (если получаем обычную эластичность спроса (по Маршаллу) на й продукт по цене

– перекрёстная эластичность спроса (по Хиксу) на й продукт по цене ого продукта (если получаем обычную эластичность спроса (по Хиксу) на й продукт по цене

эластичность спроса по доходу,

доля дохода потребителя, который он тратит на приобретение ого продукта.

Таким образом получено уравнение (точнее уравнения) Слуцкого в эластичностях

(1.5.11)

(в общем случае