Классическая статистическая модель.

Наиболее полно в математической статистике изучена классическая статистическая модель.

Определение.

Классической статистической моделью называется статистическая модель, в которой данные представляют собой числовую выборку

Эту выборку называют выборкой из распределения.

Оцениванию подлежит в этом случае неизвестная мера на прямой. Так как мераоднозначно определяется функцией распределения, то естественно следующее определение.

Плотность данных записывается в виде

где - плотность одного наблюдения.

Эмпирическая функция распределения

Определение.

Эмпирической функцией распределения называется случайная величина

Эмпирическая функция распределения является значением эмпирической меры на множестве и, следовательно, обладает следующими свойствами

1. Для любого фиксированного набора данных она является функцией распределения.

2. Среднее значение данной функции распределения для любого , вычисленное в предположении, что неизвестная мера равна, равно

3. для любой меры .

Эмпирическая функция распределения реализует идею подстановки, и обладает также еще двумя важными свойствами, которые приводятся без доказательства.

Теорема Гливенко.

Теорема Колмогорова.

Если функция распределения данных непрерывна, то

,

где

Распределение случайной величины называется распределением Колмогорова, а функция распределения называется функцией распределения Колмогорова.

Выборочные характеристики

Следующие функции от выборки называются выборочными характеристиками. Это

1. Выборочное среднее

2. Выборочная дисперсия

3. Несмещенная выборочная дисперсия

4. Минимальная порядковая статистика

5. Максимальная порядковая статистика

6. -тая порядковая статистика

7. Медиана

8. Вариационный ряд выборки

Эти характеристики позволяют компактно представить часть информации, содержащейся в выборке, и часто естественным образом возникают при решении статистических задач.

Свойства выборочных характеристик

Пользуясь методами теории вероятностей (свойства математического ожидания и дисперсии, закон больших чисел и центральная предельная теорема), нетрудно получить (в априорном предположении о существовании достаточного числа моментов у случайной величины ) следующие свойства выборочных характеристик.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. Если функция распределения данных непрерывна, то при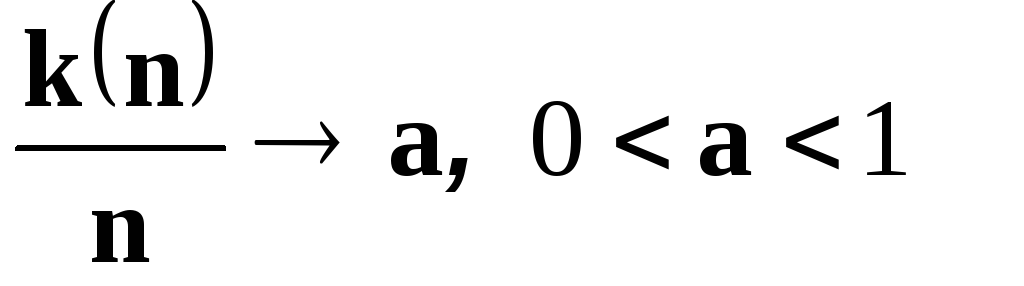 где- так называемая- квантиль, т. е. корень уравнения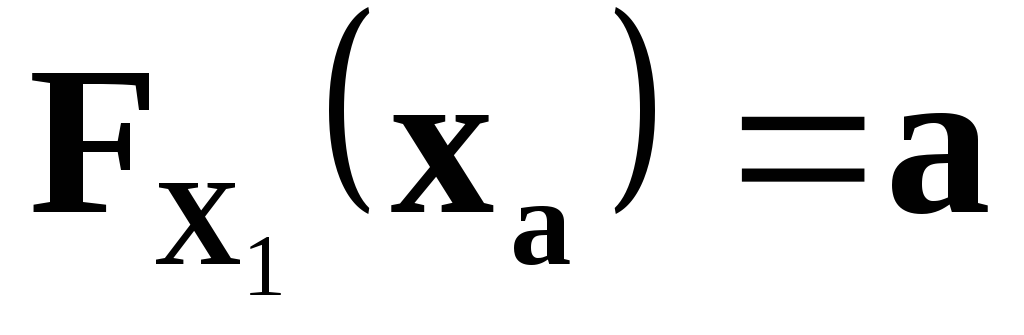

Моделирование выборок на компьютере

Моделирование числовых выборок на компьютере позволяет проиллюстрировать основные теоремы и методы классической статистики и рассчитать те характеристики статистических процедур, теоретический расчет которых затруднителен или невозможен.

Основная задача моделирования в этом случае – моделирование последовательности независимых значений некоторой числовой случайной величины (моделирование конкретного распределения). Обычно эту задачу разбивают на два этапа. Сначала моделируют последовательность значений базовой случайной величины, обычно равномерно распределенной на отрезке , затем преобразуют эту последовательность.

Датчик случайных чисел

Датчиком случайных чисел обычно называют программу, подпрограмму или функцию, которая обеспечивает построение последовательности чисел, моделирующих выборку из равномерного распределения на отрезке. В языках программирования эти функции обычно называются так: rand(), random() и т.п. Теория построения таких функций изложена, например, в книге Кнута «Искусство программирования для ЭВМ», том 2.

Последовательность независимых равномерно распределенных чисел на отрезке будем обозначать