
4 шпоргалки по Терверу / шпоры по терверу3
.doc
Гипергеометрическое
распределение.
Пусть имеется
совокупность элементов 2х типов, из А
элемента 1го типа и В элемента 2го типа
(например белые и чёрные шары). Из этой
совокупности без возвращения набирается
n
– элементов, n<=a+b.
Рассмотрим св КСИ, равную числу элементов
1го типа, попавших в выборку. Из
совокупности числа элементов (2х типов,
n
штук) набираем выборку объёмом n.
P(ξ=k)={число
элементов 1го типа равно k}=
Распределение
Пуассона П(λ).
О.: св КСИ имеет
распределение Пуассона с параметром
λ (П(λ)), если вероятность того, что ε
принимает значение к равна:
0 1 2 … K P0 P1 P2 … Pk
(Условие
нормировки
Найдём математическое
ожидание в распределении Пуассона:
Дисперсией св КСИ
называется число, определяемое как:
Дисперсия – мера
разброса значений св около своего
математического ожидания.
О.: Ковариацией св
ξ и ή называется число, определяемое
как:
Если св ξ и ή
независимы, то ковариация между ними
равна нулю и тогда независимы любые
функции от них.
Если φ(ξ) ψ(ή)
независимы, то независимы ξ-М ξ и ή-М ή.
По свойствам
математических ожиданий, математическое
ожидание произведения 2х независимых
св равно произведению их математических
ожиданий.
Если величины
зависимы, то ковариация может быть
равна пустому множеству (или нулю, хрен
разберёт что он пишет), т.е. если cov(ξ,ή)=0
это не означает, что св ξ и ή независимы.
О.: Коэффициентом
корреляции двух св ξ и ή называют число:
Свойства дисперсий.
Для любой св ξ
Dξ>=0,
при этом равентсво (Dξ=0)
возможно
тогда и только тогда, когда ξ=const.
Пусть ξ=const,
Mξ=const,
Dξ=M(C-C)2=0,
по последнему свойству матожиданий
(интересно какое это последнее свойство)
ξ –
Мξ=0,
ξ=Мξ=const.
Для любых св ξ
D(Cξ)=C2Dξ.
Для любых св ξ
D(ξ+C)=Dξ.
Если св ξ
и ή независимы, то
D(ξ+ή)=Dξ+Dή(2)
D(ξ+ή)=M[(ξ+ή)-M(ξ+ή)]2=M[ξ-Mξ+ή-Mξ(?)]2=
=M(ξ-Mξ)2+2M(ξ-Mξ)(ή-Mή)+M(ή-Mή)=Dξ+Dή.
Для произвольных
св ξ
и ή D(ξ+ή)=Dξ+Dή+2cov(ξ,ή).
Заметим, что формула
(2) верна не только для 2х независимых
величин, а для любых величин, у которых
ковариация равна пустому множеству
(или нулю), такие величины называются
некоррелированными.
Следствие: Для
любых св КСИ дисперсия их суммы равна:
Для любых св ξ
Dξ=Mξ2-(Mξ)2.
Доказательство:
Dξ=M(ξ-Mξ)2=M(ξ2-2(Mξ)ξ+(Mξ)2)=Mξ2-(2Mξ)(Mξ)+(Mξ)2=Mξ2-(Mξ)2.
Следствие: Для
любых св ξ
Mξ2>=(Mξ)2.
Свойства cov
и коэффициентов корреляций.
Для любых св ξ
и ή cov(ξ,ή)=M(ξή)-(Mξ)(Mή),
если ξ
и ή – независимые,
то cov(ξ,ή)=0.
cov(ξ,ή)>0
(≠0→ξ
и ή
– зависимые)
с ростом одной величины, вторая
увеличивается. Такие величины называются
положительным коррелированием.
Если cov(ξ,ή)<0→с
ростом одной величины, вторая уменьшается.
Свойства cov
и коэффициентов корреляций.
Для любых св ξ
и ή cov(ξ,ή)=M(ξή)-(Mξ)(Mή),
если ξ
и ή – независимые,
то cov(ξ,ή)=0.
cov(ξ,ή)>0
(≠0→ξ
и ή
– зависимые)
с ростом одной величины, вторая
увеличивается. Такие величины называются
положительным коррелированием.
Если cov(ξ,ή)<0→с
ростом одной величины, вторая уменьшается.
Характеристические
функции.
Для любых св
существует характеристическая функция,
определяемая как функция действительной
переменной t.
gξ(t)=Meitξ.
Если св ξ
дискретная, то
Если св ξ
абсолютно непрерывна с плоскостью
распределения вероятностей f(x),
то:
Свойства
характеристических функций.
gξ(0)=1;
Igξ(t)I<=1.
У св ξ
характеристическая функция есть gξ(t),
а св ή=aξ+b,
то характеристическая функция св ή
равна
Если св ξ1,
ξ2,...,ξn
независимы,
то характеристическая функция
Характеристическая
функция (ХФ) однозначно определяет
закон распределения св.
Если св ξ
целочисленная и её производящая функция
равна φξ(z),
то её характеристическая функция равна
LordCamel
шпоры
страница 5
О.: Говорят, что
последовательные функции распределения
F1(X),
F2(X)…
слабосходятся к функции F(X),
если Fn(X)→F(X)
во всех
точках непрерывности функции F(X).
Между слабой
сходимостью распределений и поточечной
сходимости ХФ существует взаимо-однозначное
соответствие, которое даётся теоремой:
Теорема
непрерывности характеристических
функций:
Пусть ξ1,
ξ2... есть последовательность св,
F1(X),
F2(X)…
есть последовательность их функций
распределения, а g1(t),
g2(t)…
есть последовательность их
характеристических функций, [обозначается
Если при любом t
gn(t)
сходится к некоторой функции g(t)
gn(t)→g(t)
при n→∞,
которая непрерывна в т.0=t,
то утверждение:
А.) g(t)
– есть характеристическая функция для
некоторого закона распределения,
задаваемого функцией распределения
F(X).
Б.) Fn(X)
2.) Если Fn(X)
Виды сходимости
св. Неравенство Чебышёва.
Сходимость по
вероятности.
Пусть св ξ
и ξ1 ξ2 ... определены
для одного и того же эксперимента.
Говорят, что
последовательность св ξ1,
ξ2... сходится
по вероятности к св ξ,
если для любого ε>0
вероятность того, что
Сходимость по
распределению. Обозначим через
F(x)=P(ξ<x),
а через
Fn(x)=P{ξn<x},
n=1,2,3…
О.: Говорят, что
последовательность св ξ1,
ξ2... сходится
по распределению к св ξ,
если последовательность функций
распределения слабо сходится к F(X).
Лаплас:
Как распределена
св μ без нормировки?
Неравенство
Чебышёва.
Т1.: Пусть св ξ
– неотрицательна и у неё существует
математическое ожидание и дисперсия.
Тогда для
Доказательство:
Пусть св ξ
– непрерывна и
задаётся плотностью распределения
вероятностей f(x).
Т2.: (Неравенство
Чебышёва): Для любой св ξ,
у которой существует Mξ
и Dξ,
для люого ε,
вероятность того, что св будет отличаться
от Mξ
более, чем на ξ
не превосходит Dξ/ε2.
Доказательство:
С помощью неравенства
Чебышёва можно оценить отклонения св
от своего математического ожидания
даже не зная закон её распределения.
Пример: Пусть надо
измерить диаметр лунного диска используя
фото луны, полученные с телескопа. Пусть
истинное значение диаметра равно а.
Пусть ξ
– полученный результат.
И Мξ=а.
Возьмём n
наблюдений:
Закон больших
чисел.
Пусть ξ1,
ξ2... есть последовательность
св, связанная с одним и тем же экспериментом
и имеющих математическое ожидание.
Говорят, что к последовательности
применим закон больших чисел (ЗБЧ), если
для любого ε>0,
вероятность
ЗБЧ – это совокупность
теорем, устанавливающих условия, при
которых для последовательности св
выполняется соотношение (1).
Теорема Бернулли:
Пусть св μт
– число успехов в n
испытаниях Бернулли, с вероятностью
успеха в одном испытании, равной p
(0<p<1).
Тогда для любого ε>0
Доказательство:
LordCamel
шпоры
страница 6 ,
к=0,1,…,а.
,
к=0,1,…,а.
![]() целое
неотрицательное число.
целое
неотрицательное число.
![]() )
)![]()
![]()
![]() .
.![]() .
.
![]()
![]() .
.

![]()
![]() .
.
![]() .
.
![]() .
.
![]() ],
тогда:
],
тогда:
![]() F(X)
F(X)![]() F(X),
где F(X)
– функция распределения, то gn(t)→g(t),
где g(t)
– характеристическая функция, которая
соответствует закону распределения с
функцией распределения F(X).
F(X),
где F(X)
– функция распределения, то gn(t)→g(t),
где g(t)
– характеристическая функция, которая
соответствует закону распределения с
функцией распределения F(X).
![]()
![]() .
.
![]()

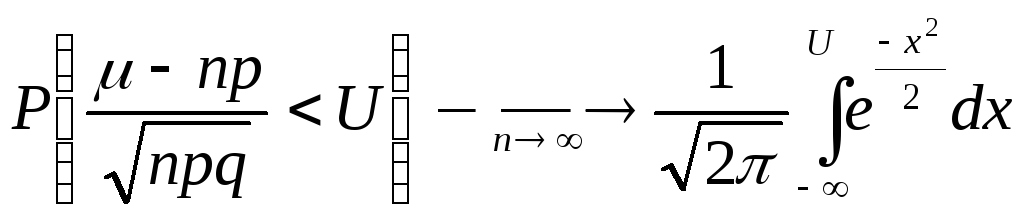 .
.![]() смысл
Лапласа.
смысл
Лапласа.![]() вероятность того, что св примет значение
не меньше, чем ε
ограничена Mξ/ξ.
(P{ξ>=ε}<=Mξ/ξ.
вероятность того, что св примет значение
не меньше, чем ε
ограничена Mξ/ξ.
(P{ξ>=ε}<=Mξ/ξ.![]()
![]() .
.
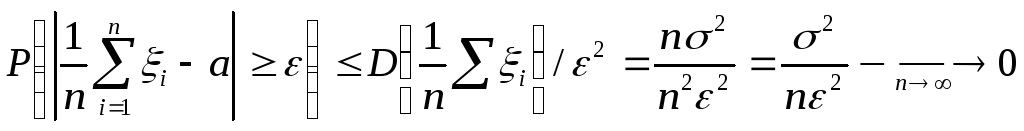 ,
,
![]() .
. .
.![]() т.е. последовательность св μn/n
сходится к числу р по
т.е. последовательность св μn/n
сходится к числу р по
![]() .
.

