
Вероятностные пространства
.pdfDZșȎȐȎ 1. ǰdzǾǼȍȀǻǼǿȀǻȉdz ǽǾǼǿȀǾǮǻǿȀǰǮ
§1.1. ȋǹdz dzǻȀȉ ǸǼ ǯǶǻǮȀǼǾǶǸǶ
ǰ ȠȓȜȞȖȖ ȐȓȞȜȭȠțȜȟȠȓȗ ȥȎȟȠȜ ȝȞȖȣȜȒȖȠȟȭ ȖȚȓȠȪ ȒȓșȜ ȟ ȕȎȒȎȥȎȚȖ, Ȑ ȘȜȠȜȞȩȣ țȓȜȏȣȜȒȖȚȜ ȝȜȒȟȥȖȠȩȐȎȠȪ ȥȖȟșȜ ȐȜȕȚȜȔțȩȣ ȟȝȜȟȜȏȜȐ ȟȜȐȓȞȦȓțȖȭ ȘȎȘȖȣ-șȖȏȜ ȒȓȗȟȠȐȖȗ. ǵȎȒȎȥȖ ȠȎȘȜȑȜ ȠȖȝȎ țȎȕȩȐȎȬȠȟȭ ȘȜȚȏȖțȎȠǝȞțȩȚȖ, Ȏ ȞȎȕȒȓș ȚȎȠȓȚȎȠȖȘȖ, ȕȎțȖȚȎȬȧȖȗȟȭ ȞȓȦȓțȖȓȚ ȠȎȘȖȣ ȕȎȒȎȥ, — ȘȜȚȏȖțȎȠǝȞȖȘȜȗ. ǿȢȜȞȚȡșȖȞȡȓȚ ȒȐȎ ȡțȖȐȓȞȟȎșȪțȩȣ ȝȞȎȐȖșȎ, ȝȞȖȚȓțȭȓȚȩȣ ȝȞȖ ȞȓȦȓțȖȖ ȘȜȚȏȖțȎȠȜȞțȩȣ ȕȎȒȎȥ.
ǽǾǮǰǶǹǼ ǽǾǼǶǵǰdzDzdzǻǶȍ. ǽȡȟȠȪ ȠȞȓȏȡȓȠȟȭ ȐȩȝȜșțȖȠȪ ȜȒțȜ ȕȎ ȒȞȡȑȖȚ ȘȎȘȖȓ-șȖȏȜ m ȒȓȗȟȠȐȖȗ. dzȟșȖ ȝȓȞȐȜȓ ȒȓȗȟȠȐȖȓ ȚȜȔțȜ ȐȩȝȜșțȖȠȪ n1 ȟȝȜȟȜȏȎȚȖ, ȐȠȜȞȜȓ ȒȓȗȟȠȐȖȓ — n2 ȟȝȜȟȜȏȎȚȖ Ȗ ȠȎȘ ȒȜ m -ȑȜ ȒȓȗȟȠ-
ȐȖȭ, ȘȜȠȜȞȜȓ ȚȜȔțȜ ȐȩȝȜșțȖȠȪ nm ȟȝȜȟȜȏȎȚȖ, ȠȜ Ȑȟȓ m ȒȓȗȟȠȐȖȗ ȚȜȑȡȠ ȏȩȠȪ ȐȩȝȜșțȓțȩ n1n2 L nm
ȟȝȜȟȜȏȎȚȖ.
ǽǾǮǰǶǹǼ ǿȁ ȉ. ǽȡȟȠȪ ȠȞȓȏȡȓȠȟȭ ȐȩȝȜșțȖȠȪ ȜȒțȜ Ȗȕ ȘȎȘȖȣ-șȖȏȜ m ȒȓȗȟȠȐȖȗ, ȐȕȎȖȚțȜ ȖȟȘșȬȥȎȬȧȖȣ ȒȞȡȑ ȒȞȡȑȎ. dzȟșȖ ȝȓȞȐȜȓ ȒȓȗȟȠȐȖȓ ȚȜȔțȜ ȐȩȝȜșțȖȠȪ n1 ȟȝȜȟȜȏȎȚȖ, ȐȠȜȞȜȓ ȒȓȗȟȠȐȖȓ — n2 ȟȝȜȟȜ-
ȏȎȚȖ Ȗ ȠȎȘ ȒȜ m -ȑȜ ȒȓȗȟȠȐȖȭ, ȘȜȠȜȞȜȓ ȚȜȔțȜ ȐȩȝȜșțȖȠȪ nm ȟȝȜȟȜȏȎȚȖ, ȠȜ ȐȩȝȜșțȖȠȪ ȜȒțȜ Ȗȕ ȫȠȖȣ m ȒȓȗȟȠȐȖȗ ȚȜȔțȜ (n1 + n2 + L + nm ) ȟȝȜȟȜȏȎȚȖ.
ǻȎȝȜȚțȖȚ ȝȜțȭȠȖȓ ȢȎȘȠȜȞȖȎșȎ, ȎȘȠȖȐțȜ ȖȟȝȜșȪȕȡȓȚȜȓ Ȑ ȘȜȚȏȖțȎȠȜȞȖȘȓ. ȂȎȘȠȜȞȖȎșȜȚ țȎȠȡȞȎșȪțȜȑȜ ȥȖȟșȎ n țȎȕȩȐȎȓȠȟȭ ȥȖȟșȜ
n ! = n(n - 1)(n - 2)L 3ɑ2 ɑ1. |
(1.1) |
ǽȜ ȜȝȞȓȒȓșȓțȖȬ, ȢȎȘȠȜȞȖȎșȜȚ țȡșȭ ȭȐșȭȓȠȟȭ ȓȒȖțȖȤȎ: |
|
0! = 1. |
(1.2) |
ǾȎȟȟȚȜȠȞȖȚ țȓȘȜȠȜȞȜȓ ȚțȜȔȓȟȠȐȜ S , ȟȜȟȠȜȭȧȓȓ Ȗȕ n ȞȎȕșȖȥțȩȣ ȫșȓȚȓțȠȜȐ. ǽȡȟȠȪ 1 „ |
k „ n . |
ǻȎȕȜȐȮȚ ȚțȜȔȓȟȠȐȜ, ȟȜȟȠȜȭȧȓȓ Ȗȕ k ȫșȓȚȓțȠȜȐ, ȡȝȜȞȭȒȜȥȓțțȩȚ, ȓȟșȖ ȘȎȔȒȜȚȡ ȫșȓȚȓțȠȡ ȫȠȜȑȜ ȚțȜȔȓȟȠȐȎ ȝȜȟȠȎȐșȓțȜ Ȑ ȟȜȜȠȐȓȠȟȠȐȖȓ ȥȖȟșȜ ȜȠ 1 ȒȜ k , ȝȞȖȥȮȚ ȞȎȕșȖȥțȩȚ ȫșȓȚȓțȠȎȚ ȚțȜȔȓȟȠȐȎ ȟȜȜȠȐȓȠȟȠȐȡȬȠ ȞȎȕțȩȓ ȥȖȟșȎ.
ǾȎȕȚȓȧȓțȖȭȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ ȝȜ k țȎȕȩȐȎȬȠȟȭ ȡȝȜȞȭȒȜȥȓțțȩȓ ȝȜȒȚțȜȔȓȟȠȐȎ ȚțȜȔȓȟȠȐȎ S , ȟȜȟȠȜȭȧȖȓ Ȗȕ k ȞȎȕșȖȥțȩȣ ȫșȓȚȓțȠȜȐ Ȗ ȜȠșȖȥȎȬȧȖȓȟȭ ȒȞȡȑ ȜȠ ȒȞȡȑȎ ȟȜȟȠȎȐȜȚ ȫșȓȚȓțȠȜȐ ȖșȖ ȝȜȞȭȒ-
ȘȜȚ Ȗȣ ȞȎȟȝȜșȜȔȓțȖȭ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ȅȖȟșȜ ȞȎȕȚȓȧȓțȖȗ Ȗȕ n |
ȫșȓȚȓțȠȜȐ ȝȜ k ȞȎȐțȜ |
|
|
|
|||||||||||
|
Ank = |
|
n ! |
= n |
(n |
- 1)(n - 2)L (n - |
k + 1) . |
|
(1.3) |
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
(n - k)! |
|
|
|
|
|
|
|
|
|||
ǽȓȞȓȟȠȎțȜȐȘȎȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ țȎȕȩȐȎȬȠȟȭ ȞȎȕȚȓȧȓțȖȭ Ȗȕ n |
ȫșȓȚȓțȠȜȐ ȝȜ n , Ƞ. ȓ. ȡȝȜȞȭȒȜȥȓț- |
||||||||||||||
țȩȓ ȝȜȒȚțȜȔȓȟȠȐȎ ȚțȜȔȓȟȠȐȎ S , ȟȜȟȠȜȭȧȖȓ Ȗȕ Ȑȟȓȣ ȫșȓȚȓțȠȜȐ ȒȎțțȜȑȜ ȚțȜȔȓȟȠȐȎ Ȗ ȜȠșȖȥȎȬȧȖȓ- |
|||||||||||||||
ȟȭ ȒȞȡȑ ȜȠ ȒȞȡȑȎ ȠȜșȪȘȜ ȝȜȞȭȒȘȜȚ Ȗȣ ȞȎȟȝȜșȜȔȓțȖȭ. |
|
|
|
||||||||||||
ȅȖȟșȜ ȝȓȞȓȟȠȎțȜȐȜȘ Ȗȕ n |
ȫșȓȚȓțȠȜȐ ȞȎȐțȜ |
|
|
|
|
|
|||||||||
|
|
|
|
Pn |
= n ! = n(n - |
|
1)(n - 2)L 3 ɑ2 ɑ1 . |
|
(1.4) |
||||||
ǿȜȥȓȠȎțȖȭȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ ȝȜ k |
țȎȕȩȐȎȬȠȟȭ ȝȜȒȚțȜȔȓȟȠȐȎ ȚțȜȔȓȟȠȐȎ S , ȟȜȟȠȜȭȧȖȓ Ȗȕ k |
ȞȎȕ- |
|||||||||||||
șȖȥțȩȣ ȫșȓȚȓțȠȜȐ Ȗ ȜȠșȖȥȎȬȧȖȓȟȭ ȒȞȡȑ ȜȠ ȒȞȡȑȎ ȠȜșȪȘȜ ȟȜȟȠȎȐȜȚ ȫșȓȚȓțȠȜȐ. |
|
||||||||||||||
ȅȖȟșȜ ȟȜȥȓȠȎțȖȗ Ȗȕ n ȫșȓȚȓțȠȜȐ ȝȜ k ȞȎȐțȜ |
|
|
|
||||||||||||
k |
|
|
Ank |
n ! |
|
|
|
|
n(n - 1)(n - 2)L (n - k + 1) |
. |
(1.5) |
||||
Cn |
= |
|
|
= |
|
|
|
|
= |
|
|
|
|||
|
|
|
|
|
|
k(k - 1)(k - 2) L 3 ɑ2 ɑ1 |
|||||||||
|
|
|
Pk |
k !(n - k)! |
|
|
|
|
|||||||
ǾȎȕȚȓȧȓțȖȭȚȖ ȟ ȝȜȐȠȜȞȓțȖȭȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ ȝȜ k țȎȕȩȐȎȬȠȟȭ ȡȝȜȞȭȒȜȥȓțțȩȓ ȝȜȒȚțȜȔȓȟȠȐȎ ȚțȜȔȓȟȠȐȎ S , ȟȜȟȠȜȭȧȖȓ Ȗȕ k ȫșȓȚȓțȠȜȐ, ȟȞȓȒȖ ȘȜȠȜȞȩȣ ȚȜȑȡȠ ȜȘȎȕȎȠȪȟȭ ȜȒȖțȎȘȜȐȩȓ, Ȗ ȜȠșȖȥȎȬȧȖȓȟȭ ȒȞȡȑ ȜȠ ȒȞȡȑȎ ȟȜȟȠȎȐȜȚ ȫșȓȚȓțȠȜȐ ȖșȖ ȝȜȞȭȒȘȜȚ Ȗȣ ȞȎȟȝȜșȜȔȓțȖȭ.
ȅȖȟșȜ ȞȎȕȚȓȧȓțȖȗ ȟ ȝȜȐȠȜȞȓțȖȭȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ ȝȜ k ȞȎȐțȜ
%k |
k |
. |
(1.6) |
An = n |
|
5
ǿȜȥȓȠȎțȖȭȚȖ ȟ ȝȜȐȠȜȞȓțȖȭȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ ȝȜ k țȎȕȩȐȎȬȠȟȭ ȝȜȒȚțȜȔȓȟȠȐȎ ȚțȜȔȓȟȠȐȎ S , ȟȜ-
ȟȠȜȭȧȖȓ Ȗȕ k ȫșȓȚȓțȠȜȐ, ȟȞȓȒȖ ȘȜȠȜȞȩȣ ȚȜȑȡȠ ȜȘȎȕȎȠȪȟȭ ȜȒȖțȎȘȜȐȩȓ, Ȗ ȜȠșȖȥȎȬȧȖȓȟȭ ȒȞȡȑ ȜȠ
ȒȞȡȑȎ ȠȜșȪȘȜ ȟȜȟȠȎȐȜȚ ȫșȓȚȓțȠȜȐ. |
|
|
|
|
|
|
|
|
|
|
|
ȅȖȟșȜ ȟȜȥȓȠȎțȖȗ ȟ ȝȜȐȠȜȞȓțȖȭȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ ȝȜ k |
ȞȎȐțȜ |
|
|||||||||
%k |
k |
|
(n + k - 1)! |
|
(n + k - 1)(n + k - 2)L n |
|
|||||
Cn |
= Cn + k- 1 |
= |
|
|
|
= |
|
|
|
|
|
|
k !(n - 1)! |
|
|
k(k - |
1)(k - 2)L 3 ɑ2 ɑ1 . |
(1.7) |
|||||
|
|
|
|
|
|
||||||
ǼȠȚȓȠȖȚ, ȥȠȜ ȢȜȞȚȡșȩ (1.4) – (1.7) ȟȜȣȞȎțȭȬȠ ȟȚȩȟș Ȗ ȜȟȠȎȬȠȟȭ ȟȝȞȎȐȓȒșȖȐȩȚȖ Ȗ ȝȞȖ k = 0 . dzȟșȖ ȐȜ ȚțȜȔȓȟȠȐȓ S , ȟȜȟȠȜȭȧȓȚ Ȗȕ n ȫșȓȚȓțȠȜȐ, ȓȟȠȪ ȠȜșȪȘȜ m ȞȎȕșȖȥțȩȣ ȫșȓȚȓțȠȜȐ, ȠȜ ȝȓȞȓȟȠȎțȜȐȘȎȚȖ ȟ ȝȜȐȠȜȞȓțȖȭȚȖ Ȗȕ n ȫșȓȚȓțȠȜȐ țȎȕȩȐȎȬȠȟȭ ȡȝȜȞȭȒȜȥȓțțȩȓ ȝȜȒȚțȜȔȓȟȠȐȎ ȚțȜȔȓȟȠȐȎ
S , Ȑ ȘȜȠȜȞȩȓ ȝȓȞȐȩȗ ȫșȓȚȓțȠ ȚțȜȔȓȟȠȐȎ S |
ȐȣȜȒȖȠ n1 ȞȎȕ, ȐȠȜȞȜȗ ȫșȓȚȓțȠ — n2 ȞȎȕ Ȗ ȠȎȘ ȒȜ |
||||||
m -ȑȜ ȫșȓȚȓțȠȎ, ȘȜȠȜȞȩȗ ȐȣȜȒȖȠ nm ȞȎȕ (n1 + n2 + L + nm = n ). |
|
|
|||||
ȅȖȟșȜ ȝȓȞȓȟȠȎțȜȐȜȘ ȟ ȝȜȐȠȜȞȓțȖȭȚȖ Ȗȕ n |
ȫșȓȚȓțȠȜȐ, Ȑ ȘȜȠȜȞȩȓ ȝȓȞȐȩȗ ȫșȓȚȓțȠ ȚțȜȔȓȟȠȐȎ S |
||||||
ȐȣȜȒȖȠ n1 ȞȎȕ, ȐȠȜȞȜȗ ȫșȓȚȓțȠ — n2 ȞȎȕ Ȗ ȠȎȘ ȒȜ |
m -ȑȜ ȫșȓȚȓțȠȎ, ȘȜȠȜȞȩȗ ȐȣȜȒȖȠ |
nm ȞȎȕ |
|||||
(n1 + n2 + L + nm = n ), ȞȎȐțȜ |
|
|
|
|
|
|
|
% |
|
|
n ! |
. |
(1.8) |
||
Pn (n1,n2,...,nm ) = |
|
|
|
||||
n1 !n2 !L nm ! |
|||||||
|
|
|
|
||||
1. ǺȎȦȎ ȝȜȟȟȜȞȖșȎȟȪ ȟ ǽȓȠȓȗ Ȗ țȓ ȣȜȥȓȠ ȓȣȎȠȪ ȟ țȖȚ Ȑ ȜȒțȜȚ ȎȐȠȜȏȡȟȓ. ǼȠ ȜȏȧȓȔȖȠȖȭ ȒȜ ȖțȟȠȖȠȡȠȎ ȟ 7 ȒȜ 8 ȥ ȜȠȝȞȎȐșȭȓȠȟȭ ȝȭȠȪ ȎȐȠȜȏȡȟȜȐ. ǻȓ ȡȟȝȓȐȦȖȗ țȎ ȝȜȟșȓȒțȖȗ Ȗȕ ȫȠȖȣ ȎȐȠȜȏȡȟȜȐ ȜȝȎȕȒȩȐȎȓȠ țȎ șȓȘȤȖȬ. ǿȘȜșȪȘȖȚȖ ȟȝȜȟȜȏȎȚȖ ǺȎȦȎ Ȗ ǽȓȠȭ ȚȜȑȡȠ ȒȜȓȣȎȠȪ ȒȜ ȖțȟȠȖȠȡȠȎ Ȑ ȞȎȕțȩȣ ȎȐȠȜȏȡȟȎȣ Ȗ țȓ ȜȝȜȕȒȎȠȪ țȎ șȓȘȤȖȬ?
ǾdzȆdzǻǶdz. ǽȓȠȭ ȚȜȔȓȠ ȒȜȓȣȎȠȪ ȒȜ ȖțȟȠȖȠȡȠȎ n1= 5 ȞȎȕșȖȥțȩȚȖ ȟȝȜȟȜȏȎȚȖ (țȎ ȜȒțȜȚ Ȗȕ ȝȭȠȖ ȎȐȠȜȏȡȟȜȐ), ȝȞȖ ȫȠȜȚ ǺȎȦȓ ȜȟȠȎȮȠȟȭ ȠȜșȪȘȜ n2 = 4 ȟȝȜȟȜȏȎ (ȠȎȘ ȘȎȘ ȜȒȖț Ȗȕ ȎȐȠȜȏȡȟȜȐ ȕȎțȭȠ ǽȓ-
Ƞȓȗ). ȀȎȘȖȚ ȜȏȞȎȕȜȚ, ȝȜ ȝȞȎȐȖșȡ ȝȞȜȖȕȐȓȒȓțȖȭ ȡ ǽȓȠȖ Ȗ ǺȎȦȖ ȓȟȠȪ n1n2 = 5ɑ4 = 20 ȞȎȕșȖȥțȩȣ
ȟȝȜȟȜȏȜȐ ȒȜȏȞȎȠȪȟȭ ȒȜ ȖțȟȠȖȠȡȠȎ Ȑ ȞȎȕțȩȣ ȎȐȠȜȏȡȟȎȣ Ȗ țȓ ȜȝȜȕȒȎȠȪ țȎ șȓȘȤȖȬ.
2. ǰ ȖțȢȜȞȚȎȤȖȜțțȜ-ȠȓȣțȜșȜȑȖȥȓȟȘȜȚ ȡȝȞȎȐșȓțȖȖ ȏȎțȘȎ ȞȎȏȜȠȎȬȠ ȠȞȖ ȎțȎșȖȠȖȘȎ, ȒȓȟȭȠȪ ȝȞȜȑȞȎȚȚȖȟȠȜȐ Ȗ 20 ȖțȔȓțȓȞȜȐ. Dzșȭ ȟȐȓȞȣȡȞȜȥțȜȗ ȞȎȏȜȠȩ Ȑ ȝȞȎȕȒțȖȥțȩȗ ȒȓțȪ țȎȥȎșȪțȖȘ ȡȝȞȎȐșȓțȖȭ ȒȜșȔȓț ȐȩȒȓșȖȠȪ ȜȒțȜȑȜ ȟȜȠȞȡȒțȖȘȎ. ǿȘȜșȪȘȜ ȟȝȜȟȜȏȜȐ ȟȡȧȓȟȠȐȡȓȠ ȡ țȎȥȎșȪțȖȘȎ ȡȝȞȎȐșȓțȖȭ?
ǾdzȆdzǻǶdz. ǻȎȥȎșȪțȖȘ ȡȝȞȎȐșȓțȖȭ ȚȜȔȓȠ ȜȠȜȏȞȎȠȪ ȜȒțȜȑȜ ȎțȎșȖȠȖȘȎ n1 = 3 ȟȝȜȟȜȏȎȚȖ, ȜȒțȜȑȜ ȝȞȜȑȞȎȚȚȖȟȠȎ — n2 = 10 ȟȝȜȟȜȏȎȚȖ, Ȏ ȜȒțȜȑȜ ȖțȔȓțȓȞȎ — n3 = 20 ȟȝȜȟȜȏȎȚȖ. ǽȜȟȘȜșȪȘȡ ȝȜ ȡȟ-
șȜȐȖȬ ȕȎȒȎȥȖ țȎȥȎșȪțȖȘ ȡȝȞȎȐșȓțȖȭ ȚȜȔȓȠ ȐȩȒȓșȖȠȪ șȬȏȜȑȜ Ȗȕ ȟȐȜȖȣ ȟȜȠȞȡȒțȖȘȜȐ, ȟȜȑșȎȟțȜ ȝȞȎȐȖșȡ ȟȡȚȚȩ ȡ țȓȑȜ ȟȡȧȓȟȠȐȡȓȠ n1 + n2 + n3 = 3 + 10 + 20 = 33 ȞȎȕșȖȥțȩȣ ȟȝȜȟȜȏȎ ȐȩȏȞȎȠȪ ȟȜ-
ȠȞȡȒțȖȘȎ Ȓșȭ ȟȐȓȞȣȡȞȜȥțȜȗ ȞȎȏȜȠȩ.
3. ǻȎȥȎșȪțȖȘ ȟșȡȔȏȩ ȏȓȕȜȝȎȟțȜȟȠȖ ȏȎțȘȎ ȒȜșȔȓț ȓȔȓȒțȓȐțȜ ȞȎȟȟȠȎȐșȭȠȪ ȒȓȟȭȠȪ ȜȣȞȎțțȖȘȜȐ ȝȜ ȒȓȟȭȠȖ ȝȜȟȠȎȚ. ǰ Ȥȓșȭȣ ȡȟȖșȓțȖȭ ȏȓȕȜȝȎȟțȜȟȠȖ ȜȒțȎ Ȗ ȠȎ Ȕȓ ȘȜȚȏȖțȎȤȖȭ ȞȎȟȟȠȎțȜȐȘȖ ȜȣȞȎțțȖȘȜȐ ȝȜ ȝȜȟȠȎȚ țȓ ȚȜȔȓȠ ȝȜȐȠȜȞȭȠȪȟȭ ȥȎȧȓ ȜȒțȜȑȜ ȞȎȕȎ Ȑ ȚȓȟȭȤ. ȅȠȜȏȩ ȜȤȓțȖȠȪ, ȐȜȕȚȜȔțȜ șȖ ȫȠȜ, țȎȗȠȖ ȥȖȟșȜ ȞȎȕșȖȥțȩȣ ȘȜȚȏȖțȎȤȖȗ ȞȎȟȟȠȎțȜȐȘȖ ȜȣȞȎțțȖȘȜȐ.
ǾdzȆdzǻǶdz. ǽȓȞȐȩȗ ȟȝȜȟȜȏ. ǻȎ ȝȓȞȐȩȗ ȝȜȟȠ țȎȥȎșȪțȖȘ ȟșȡȔȏȩ ȏȓȕȜȝȎȟțȜȟȠȖ ȚȜȔȓȠ țȎȕțȎȥȖȠȪ șȬȏȜȑȜ Ȗȕ n1 = 10 ȜȣȞȎțțȖȘȜȐ, țȎ ȐȠȜȞȜȗ ȝȜȟȠ — șȬȏȜȑȜ Ȗȕ ȜȟȠȎȐȦȖȣȟȭ n2 = 9 ȜȣȞȎțțȖȘȜȐ Ȗ ȠȎȘ
ȒȜ ȒȓȐȭȠȜȑȜ ȝȜȟȠȎ, țȎ ȘȜȠȜȞȩȗ ȚȜȔțȜ țȎȕțȎȥȖȠȪ șȬȏȜȑȜ Ȗȕ ȜȟȠȎȐȦȖȣȟȭ n9 = 2 ȜȣȞȎțțȖȘȜȐ, ȝȞȖ ȫȠȜȚ ȜȟȠȎȐȦȖȗȟȭ n10 = 1 ȜȣȞȎțțȖȘ ȏȡȒȓȠ țȎȕțȎȥȓț țȎ ȒȓȟȭȠȩȗ ȝȜȟȠ. ǽȜȫȠȜȚȡ, ȟȜȑșȎȟțȜ ȝȞȎȐȖșȡ ȝȞȜȖȕȐȓȒȓțȖȭ, ȡ țȎȥȎșȪțȖȘȎ ȟșȡȔȏȩ ȏȓȕȜȝȎȟțȜȟȠȖ ȓȟȠȪ n1n2 L n10 = 10 ɑ9L 2 ɑ1 = 10! = 3 628 800
ȟȝȜȟȜȏȜȐ ȞȎȟȟȠȎțȜȐȘȖ ȜȣȞȎțțȖȘȜȐ ȝȜ ȝȜȟȠȎȚ. ǽȜȟȘȜșȪȘȡ ȘȜșȖȥȓȟȠȐȜ Ȓțȓȗ Ȑ ȚȓȟȭȤȓ țȓ ȝȞȓȐȩȦȎȓȠ 31, ȡ țȎȥȎșȪțȖȘȎ ȟșȡȔȏȩ ȏȓȕȜȝȎȟțȜȟȠȖ ȕȎȐȓȒȜȚȜ ȟȡȧȓȟȠȐȡȓȠ ȒȜȟȠȎȠȜȥțȜȓ ȥȖȟșȜ ȟȝȜȟȜȏȜȐ ȞȎȟȟȠȎțȜȐȘȖ ȟȐȜȖȣ ȝȜȒȥȖțȮțțȩȣ ȝȜ ȝȜȟȠȎȚ.
6
ǰȠȜȞȜȗ ȟȝȜȟȜȏ. ȅȖȟșȜ ȟȝȜȟȜȏȜȐ ȞȎȟȟȠȎțȜȐȘȖ ȒȓȟȭȠȖ ȜȣȞȎțțȖȘȜȐ ȝȜ ȒȓȟȭȠȖ ȝȜȟȠȎȚ, ȟȡȧȓȟȠȐȡȬȧȖȣ ȡ țȎȥȎșȪțȖȘȎ ȟșȡȔȏȩ ȏȓȕȜȝȎȟțȜȟȠȖ, ȜȝȖȟȩȐȎȓȠȟȭ ȥȖȟșȜȚ ȝȓȞȓȟȠȎțȜȐȜȘ Ȗȕ 10 ȫșȓȚȓțȠȜȐ, Ƞ. ȓ.
P10 = 10! = 3 628 800 .
4.ǼȝȞȓȒȓșȖȠȪ, ȟȘȜșȪȘȖȚȖ ȟȝȜȟȜȏȎȚȖ ȚȜȔțȜ ȞȎȕȚȓȟȠȖȠȪ țȎ ȦȎȣȚȎȠțȜȗ ȒȜȟȘȓ ȐȜȟȓȚȪ șȎȒȓȗ ȠȎȘ, ȥȠȜȏȩ ȜțȖ țȓ ȏȖșȖ ȒȞȡȑ ȒȞȡȑȎ.
5.ǻȜȐȩȗ ȝȞȓȕȖȒȓțȠ ȏȎțȘȎ ȒȜșȔȓț țȎȕțȎȥȖȠȪ ȒȐȡȣ țȜȐȩȣ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȜȐ Ȗȕ ȥȖȟșȎ ȒȓȟȭȠȖ ȒȖȞȓȘȠȜȞȜȐ. ǿȘȜșȪȘȜ ȟȝȜȟȜȏȜȐ ȟȡȧȓȟȠȐȡȓȠ ȡ ȝȞȓȕȖȒȓțȠȎ, ȓȟșȖ: Ȏ) ȜȒȖț Ȗȕ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȜȐ (ȝȓȞȐȩȗ) ȐȩȦȓ ȒȞȡȑȜȑȜ ȝȜ ȒȜșȔțȜȟȠȖ; ȏ) ȐȖȤȓȝȞȓȕȖȒȓțȠȩ ȝȜ ȒȜșȔțȜȟȠȖ ȞȎȐțȩ ȚȓȔȒȡ ȟȜȏȜȗ.
ǾdzȆdzǻǶdz. ǽȓȞȐȩȗ ȟȝȜȟȜȏ. Ȏ) ǽȓȞȐȜȑȜ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȎ ȚȜȔțȜ ȐȩȏȞȎȠȪ Ȗȕ n1 = 10 ȝȞȓȠȓțȒȓț-
ȠȜȐ, ȝȞȖ ȫȠȜȚ țȎ ȝȜȟȠ ȐȠȜȞȜȑȜ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȎ ȏȡȒȡȠ ȝȞȓȠȓțȒȜȐȎȠȪ n2 = 9 ȜȟȠȎȐȦȖȣȟȭ ȒȖȞȓȘȠȜ-
ȞȜȐ. ǽȜȫȠȜȚȡ, ȟȜȑșȎȟțȜ ȝȞȎȐȖșȡ ȝȞȜȖȕȐȓȒȓțȖȭ, ȡ țȜȐȜȑȜ ȝȞȓȕȖȒȓțȠȎ ȏȎțȘȎ ȓȟȠȪ n1n2 = 10 ɑ9 = 90
ȟȝȜȟȜȏȜȐ țȎȕțȎȥȓțȖȭ ȒȐȡȣ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȜȐ, ȜȒȖț Ȗȕ ȘȜȠȜȞȩȣ ȝȜȒȥȖțȭȓȠȟȭ ȒȞȡȑȜȚȡ, Ȗȕ ȥȖȟșȎ ȒȓȟȭȠȖ ȒȖȞȓȘȠȜȞȜȐ. ȏ) ǽȡȟȠȪ ȝȓȞȐȜȓ ȒȓȗȟȠȐȖȓ ȕȎȘșȬȥȎȓȠȟȭ Ȑ ȠȜȚ, ȥȠȜ ȝȞȓȕȖȒȓțȠ ȜȠȏȖȞȎȓȠ ȒȐȡȣ ȥȓșȜȐȓȘ țȎ ȒȜșȔțȜȟȠȖ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȜȐ, Ȏ ȐȠȜȞȜȓ ȒȓȗȟȠȐȖȓ — Ȑ ȠȜȚ, ȥȠȜ ȝȞȓȕȖȒȓțȠ ȑȜȐȜȞȖȠ ȜȠȜȏȞȎțțȩȚ șȬȒȭȚ, ȘȠȜ Ȗȕ țȖȣ ȭȐșȭȓȠȟȭ ȝȓȞȐȩȚ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȜȚ, Ȏ ȘȠȜ — ȐȠȜȞȩȚ. ǽȡȟȠȪ ȝȓȞȐȜȓ ȒȓȗȟȠȐȖȓ ȚȜȔțȜ ȐȩȝȜșțȖȠȪ n1 ȟȝȜȟȜȏȎȚȖ, ȐȠȜȞȜȓ ȒȓȗȟȠȐȖȓ, ȜȥȓȐȖȒțȜ, ȚȜȔțȜ ȐȩȝȜșțȖȠȪ n2 = 2 ȟȝȜȟȜ-
ȏȎȚȖ, Ȗ ȝȜ ȝȞȎȐȖșȡ ȝȞȜȖȕȐȓȒȓțȖȭ ȥȖȟșȜ ȟȝȜȟȜȏȜȐ țȎȕțȎȥȓțȖȭ ȒȐȡȣ ȐȖȤȓ-ȝȞȓȕȖȒȓțȠȜȐ, ȜȒȖț Ȗȕ ȘȜȠȜȞȩȣ ȝȜȒȥȖțȭȓȠȟȭ ȒȞȡȑȜȚȡ, Ȗȕ ȥȖȟșȎ ȒȓȟȭȠȖ ȒȖȞȓȘȠȜȞȜȐ ȟȜȟȠȎȐșȭȓȠ n1n2 = 2n1 . ǿ ȒȞȡȑȜȗ ȟȠȜȞȜ-
țȩ, Ȑ ȝȡțȘȠȓ Ȏ) Țȩ țȎȦșȖ ȫȠȜ ȥȖȟșȜ, Ȗ ȜțȜ ȜȘȎȕȎșȜȟȪ ȞȎȐțȩȚ 90, ȝȜȫȠȜȚȡ n |
|
= |
90 |
= 45. |
1 |
|
|||
|
2 |
|
||
ǰȠȜȞȜȗ ȟȝȜȟȜȏ. Ȏ) ȅȖȟșȜ ȟȝȜȟȜȏȜȐ ȐȩȏȜȞȎ ȒȐȡȣ ȘȎțȒȖȒȎȠȜȐ țȎ ȒȐȓ ȞȎȕșȖȥțȩȓ ȒȜșȔțȜȟȠȖ Ȗȕ Ȓȓ-
ȟȭȠȖ ȝȞȓȠȓțȒȓțȠȜȐ ȜȝȖȟȩȐȎȓȠȟȭ ȥȖȟșȜȚ ȞȎȕȚȓȧȓțȖȗ Ȗȕ 10 ȫșȓȚȓțȠȜȐ ȝȜ 2, Ƞ. ȓ. A102 = 90. ȏ) ȅȖȟșȜ ȟȝȜȟȜȏȜȐ ȐȩȏȜȞȎ ȒȐȡȣ ȘȎțȒȖȒȎȠȜȐ țȎ ȒȐȓ ȜȒȖțȎȘȜȐȩȓ ȒȜșȔțȜȟȠȖ Ȗȕ ȒȓȟȭȠȖ ȝȞȓȠȓțȒȓțȠȜȐ ȜȝȖȟȩ-
ȐȎȓȠȟȭ ȥȖȟșȜȚ ȟȜȥȓȠȎțȖȗ Ȗȕ 10 ȫșȓȚȓțȠȜȐ ȝȜ 2, Ƞ. ȓ. C102 = 45.
6.ǰ ȘȞȓȒȖȠțȜȚ ȜȠȒȓșȓ ȏȎțȘȎ ȞȎȏȜȠȎȬȠ ȐȜȟȓȚȪ ȥȓșȜȐȓȘ. ǿȘȜșȪȘȜ ȟȡȧȓȟȠȐȡȓȠ ȟȝȜȟȜȏȜȐ ȞȎȟȝȞȓȒȓșȖȠȪ ȚȓȔȒȡ țȖȚȖ ȠȞȖ ȝȞȓȚȖȖ: Ȏ) ȜȒȖțȎȘȜȐȜȑȜ ȞȎȕȚȓȞȎ; ȏ) ȞȎȕțȩȣ ȞȎȕȚȓȞȜȐ, ȖȕȐȓȟȠțȩȣ ȕȎȞȎțȓȓ?
7.ǼȒțȎ Ȗȕ ȐȜȬȬȧȖȣ ȟȠȜȞȜț ȕȎȣȐȎȠȖșȎ Ȑ ȝșȓț 12 ȟȜșȒȎȠ, Ȏ ȒȞȡȑȎȭ 15. ǼȝȞȓȒȓșȖȠȪ, ȟȘȜșȪȘȖȚȖ ȟȝȜȟȜȏȎȚȖ ȟȠȜȞȜțȩ ȚȜȑȡȠ ȜȏȚȓțȭȠȪ ȟȓȚȓȞȩȣ ȐȜȓțțȜȝșȓțțȩȣ.
8.ǽȓȠȭ Ȗ ǺȎȦȎ ȘȜșșȓȘȤȖȜțȖȞȡȬȠ ȐȖȒȓȜȘȎȟȟȓȠȩ. ȁ ǽȓȠȖ ȓȟȠȪ 30 ȘȜȚȓȒȖȗ, 80 ȏȜȓȐȖȘȜȐ Ȗ 7 ȚȓșȜȒȞȎȚ, ȡ ǺȎȦȖ — 20 ȘȜȚȓȒȖȗ, 5 ȏȜȓȐȖȘȜȐ Ȗ 90 ȚȓșȜȒȞȎȚ. ǿȘȜșȪȘȖȚȖ ȟȝȜȟȜȏȎȚȖ ǽȓȠȭ Ȗ ǺȎȦȎ ȚȜȑȡȠ ȜȏȚȓțȭȠȪȟȭ ȠȞȓȚȭ ȘȜȚȓȒȖȭȚȖ, ȒȐȡȚȭ ȏȜȓȐȖȘȎȚȖ Ȗ ȜȒțȜȗ ȚȓșȜȒȞȎȚȜȗ?
9.ǰ ȟȓȟȟȖȬ Ȑ ȠȓȥȓțȖȓ 20 Ȓțȓȗ ȟȠȡȒȓțȠȩ ȜȒțȜȗ ȑȞȡȝȝȩ ȒȜșȔțȩ ȟȒȎȠȪ ȝȭȠȪ ȫȘȕȎȚȓțȜȐ. ǿȘȜșȪȘȖȚȖ ȟȝȜȟȜȏȎȚȖ ȚȜȔțȜ ȟȜȟȠȎȐȖȠȪ ȞȎȟȝȖȟȎțȖȓ ȫȘȕȎȚȓțȜȐ, ȓȟșȖ: Ȏ) ȕȎȝȞȓȧȎȓȠȟȭ ȟȒȎȐȎȠȪ ȒȐȎ ȫȘȕȎȚȓțȎ Ȑ ȜȒȖț ȒȓțȪ; ȏ) ȚȓȔȒȡ ȒȐȡȚȭ ȫȘȕȎȚȓțȎȚȖ ȒȜșȔȓț ȝȞȜȗȠȖ ȣȜȠȭ ȏȩ ȜȒȖț ȒȓțȪ Ȓșȭ ȝȜȒȑȜȠȜȐȘȖ?
10.ǰ ȏȎțȘȓ ȒȓȐȭȠȪ ȡȥȞȓȒȖȠȓșȓȗ. ǾȓȑȖȟȠȞȎȤȖȜțțȩȓ ȒȜȘȡȚȓțȠȩ ȣȞȎțȭȠȟȭ Ȑ ȟȓȗȢȓ. ǿȘȜșȪȘȜ ȕȎȚȘȜȐ ȒȜșȔȓț ȖȚȓȠȪ ȟȓȗȢ, Ȗ ȟȘȜșȪȘȜ ȘșȬȥȓȗ Ș țȖȚ țȡȔțȜ ȖȕȑȜȠȜȐȖȠȪ, ȥȠȜȏȩ ȒȜȟȠȡȝ Ș ȟȜȒȓȞȔȖȚȜȚȡ ȟȓȗȢȎ ȏȩș ȐȜȕȚȜȔȓț ȠȜșȪȘȜ ȠȜȑȒȎ, ȘȜȑȒȎ ȟȜȏȓȞȮȠȟȭ țȓ Țȓțȓȓ ȦȓȟȠȖ ȡȥȞȓȒȖȠȓșȓȗ?
11.ǺȎȦȎ ȞȓȦȖșȎ ȝȜȚȖȞȖȠȪȟȭ ȟ ǽȓȠȓȗ Ȗ ȝȜȕȐȜțȖȠȪ ȓȚȡ, țȜ ȕȎȏȩșȎ ȒȐȓ ȝȜȟșȓȒțȖȣ ȤȖȢȞȩ ȓȑȜ ȠȓșȓȢȜțȎ Ȗ țȎȏȖȞȎȓȠ Ȗȣ țȎȡȒȎȥȡ. ǻȎȗȠȖ țȎȖȏȜșȪȦȓȓ ȐȜȕȚȜȔțȜȓ ȥȖȟșȜ țȓȡȒȎȥțȩȣ ȝȜȝȩȠȜȘ, ȘȜȠȜȞȩȓ ȟȒȓșȎȓȠ ǺȎȦȎ, ȝȞȓȔȒȓ ȥȓȚ ȒȜȕȐȜțȖȠȟȭ ȒȜ ǽȓȠȖ.
7
12.ǿȘȜșȪȘȜ ȎȐȠȜȚȜȏȖșȓȗ Ȑ ȜȒțȜȚ ȑȜȞȜȒȓ ȚȜȔțȜ ȜȏȓȟȝȓȥȖȠȪ ȑȜȟȡȒȎȞȟȠȐȓțțȩȚȖ ȞȓȑȖȟȠȞȎȤȖȜțțȩȚȖ ȕțȎȘȎȚȖ, ȓȟșȖ ȘȎȔȒȩȗ ȞȓȑȖȟȠȞȎȤȖȜțțȩȗ ȕțȎȘ ȟȜȟȠȜȖȠ Ȗȕ ȘȜȒȎ ȑȜȞȜȒȎ, ȠȞȮȣ ȏȡȘȐ, ȖȚȓȬȧȖȣ ȜȒȖțȎȘȜȐȜȓ țȎȥȓȞȠȎțȖȓ ȘȎȘ Ȑ ȞȡȟȟȘȜȚ, ȠȎȘ Ȗ Ȑ șȎȠȖțȟȘȜȚ ȎșȢȎȐȖȠȓ («Ǯ», «ǰ», «dz», «Ǹ», «Ǻ», «ǻ», «Ǽ», «Ǿ», «ǿ», «Ȁ», «ȁ», «ȃ»), Ȗ
ȠȞȮȣ ȤȖȢȞ?
13.DzȜȘȎȕȎȠȪ ȝȞȎȐȖșȜ ȝȞȜȖȕȐȓȒȓțȖȭ.
14.DzȜȘȎȕȎȠȪ ȝȞȎȐȖșȜ ȟȡȚȚȩ.
15.DzȜȘȎȕȎȠȪ ȟȝȞȎȐȓȒșȖȐȜȟȠȪ ȢȜȞȚȡș (1.3) – (1.5).
16.DzȜȘȎȕȎȠȪ ȞȎȐȓțȟȠȐȜ: Ckn = Cnn- k (0 „ k „ n ).
ǾdzȆdzǻǶdz. Cnk = |
n ! |
= |
|
n ! |
= Cnn |
- k . |
|||
|
|
|
|
|
|||||
k !(n- k)! |
(n- k)![n- (n- k)]! |
||||||||
|
|
|
|
||||||
17. ǾǮǰdzǻǿȀǰǼ ǽǮǿǸǮǹȍ. DzȜȘȎȕȎȠȪ ȞȎȐȓțȟȠȐȜ: Ckn + Ckn+ 1= Cnk++ 11 (0„ k< n). 18. DzȜȘȎȕȎȠȪ ȞȎȐȓțȟȠȐȜ: Cn0 + Cn1 + Cn2 + L + Cnn = 2n .
19. ǼȝȞȓȒȓșȖȠȪ, ȟȘȜșȪȘȜ ȟȡȧȓȟȠȐȡȓȠ ȐȎȞȖȎțȠȜȐ ȜȝȞȜȟȎ ȑȞȡȝȝȩ Ȗȕ ȒȓȟȭȠȖ ȟȠȡȒȓțȠȜȐ țȎ ȜȒțȜȚ ȕȎțȭȠȖȖ ȝȜ ȠȓȜȞȖȖ ȐȓȞȜȭȠțȜȟȠȓȗ, ȓȟșȖ țȖ ȜȒȖț Ȗȕ ȟȠȡȒȓțȠȜȐ țȓ ȏȡȒȓȠ ȝȜȒȐȓȞȑțȡȠ ȜȝȞȜȟȡ ȒȐȎȔȒȩ, Ȗ țȎ ȕȎțȭȠȖȖ ȚȜȔȓȠ ȏȩȠȪ ȜȝȞȜȦȓțȜ șȬȏȜȓ ȥȖȟșȜ ȟȠȡȒȓțȠȜȐ (Ȑ ȠȜȚ ȥȖȟșȓ, țȖ ȜȒȖț)?
20. DzȜȘȎȕȎȠȪ ȞȎȐȓțȟȠȐȜ: (Cn0 )2 + (Cn1 )2 + (Cn2 )2 + L + (Cnn )2 = Cn2n .
21. ǺȎȦȎ ȜȥȓțȪ șȬȏȖȠ ȝȖȞȜȔțȩȓ Ȗ ȓȔȓȒțȓȐțȜ Ȑ ȏȡșȜȥțȜȗ ȞȭȒȜȚ ȟ ȖțȟȠȖȠȡȠȜȚ ȝȜȘȡȝȎȓȠ ȦȓȟȠȪ ȝȖȞȜȔțȩȣ (ȜȒȖțȎȘȜȐȩȣ ȖșȖ ȞȎȕțȩȣ). ǰȟȓȑȜ Ȑ ȏȡșȜȥțȜȗ ȝȞȜȒȎȮȠȟȭ 11 ȟȜȞȠȜȐ ȝȖȞȜȔțȩȣ. ǿȘȜșȪȘȖȚȖ ȟȝȜȟȜȏȎȚȖ ǺȎȦȎ ȚȜȔȓȠ ȐȩȏȞȎȠȪ Ȗȕ țȖȣ ȦȓȟȠȪ ȦȠȡȘ?
ǾdzȆdzǻǶdz. ǸȎȔȒȜȚȡ țȎȏȜȞȡ ȝȖȞȜȔțȩȣ, ȘȜȠȜȞȩȓ ȐȩȏȓȞȓȠ ǺȎȦȎ, ȏȡȒȓȚ ȟȠȎȐȖȠȪ Ȑ ȟȜȜȠȐȓȠȟȠȐȖȓ ȝȜȟșȓȒȜȐȎȠȓșȪțȜȟȠȪ țȡșȓȗ Ȗ ȓȒȖțȖȤ, ȜȝȞȓȒȓșȭȓȚȡȬ ȝȜ ȟșȓȒȡȬȧȓȚȡ ȝȞȎȐȖșȡ. ǻȎȝȖȦȓȚ ȝȜȒȞȭȒ ȟȠȜșȪȘȜ ȓȒȖțȖȤ, ȟȘȜșȪȘȜ ȝȖȞȜȔțȩȣ ȝȓȞȐȜȑȜ ȐȖȒȎ ȐȩȏȞȎșȎ ǺȎȦȎ, ȒȎșȓȓ ȝȜȟȠȎȐȖȚ țȡșȪ Ȗ ȝȜȟșȓ țȓȑȜ ȕȎȝȖȦȓȚ ȘȜșȖȥȓȟȠȐȜ ȜȠȜȏȞȎțțȩȣ ȝȖȞȜȔțȩȣ ȐȠȜȞȜȑȜ ȐȖȒȎ Ȗ Ƞ. Ȓ. ǻȎȝȞȖȚȓȞ, ȘȜȚȏȖțȎȤȖȖ
«ȜȒțȜ ȝȖȞȜȔțȜȓ ȐȠȜȞȜȑȜ ȐȖȒȎ, ȠȞȖ ȝȖȞȜȔțȩȣ ȝȭȠȜȑȜ ȐȖȒȎ Ȗ ȜȒțȜ ȝȖȞȜȔțȜȓ ȐȜȟȪȚȜȑȜ ȐȖȒȎ» ȟȜȜȠȐȓȠȟȠȐȡȓȠ ȠȎȘȎȭ ȝȜȟșȓȒȜȐȎȠȓșȪțȜȟȠȪ: «010001110001000» (țȡșȖ ȜȠȒȓșȭȬȠ ȐȖȒȩ ȝȖȞȜȔțȩȣ ȒȞȡȑ ȜȠ ȒȞȡȑȎ, ȝȜȫȠȜȚȡ țȡșȪ ȝȜȟșȓ ȜȒȖțțȎȒȤȎȠȜȑȜ ȐȖȒȎ țȓ țȡȔȓț). ǽȞȖ ȫȠȜȚ ȘȎȔȒȜȚȡ țȎȏȜȞȡ ȝȖȞȜȔțȩȣ ȐȕȎȖȚțȜ ȜȒțȜȕțȎȥțȩȚ ȜȏȞȎȕȜȚ ȟȜȜȠȐȓȠȟȠȐȡȓȠ ȝȜȟșȓȒȜȐȎȠȓșȪțȜȟȠȪ, ȝȜȟȠȞȜȓțțȎȭ ȝȜ ȜȝȖȟȎțțȜȚȡ ȝȞȎȐȖșȡ. ǰȟȓ ȠȎȘȖȓ ȝȜȟșȓȒȜȐȎȠȓșȪțȜȟȠȖ ȟȜȟȠȜȭȠ, ȜȥȓȐȖȒțȜ, Ȗȕ 16 ȕțȎȘȜȐ, ȝȞȖȥȮȚ 10 Ȗȕ țȖȣ țȡșȖ, ȘȜȠȜȞȩȓ ȚȜȑȡȠ ȕȎțȖȚȎȠȪ șȬȏȜȓ ȚȓȟȠȜ. ǽȜȫȠȜȚȡ ȘȜșȖȥȓȟȠȐȜ ȟȝȜȟȜȏȜȐ ȐȩȏȜȞȎ ȝȖȞȜȔțȩȣ ȞȎȐțȜ ȘȜșȖȥȓȟȠȐȡ
Ȑȟȓȣ ȠȎȘȖȣ ȝȜȟșȓȒȜȐȎȠȓșȪțȜȟȠȓȗ, Ƞ. ȓ. ȥȖȟșȡ ȞȎȕȚȓȧȓțȖȗ ȒȓȟȭȠȖ țȡșȓȗ ȝȜ 16 ȚȓȟȠȎȚ: C1016 = 8 008.
22.ǰ ȘȜțȘȡȞȟȓ ȝȜ ȠȞȮȚ țȜȚȖțȎȤȖȭȚ ȡȥȎȟȠȐȡȬȠ ȒȓȟȭȠȪ ȘȖțȜȢȖșȪȚȜȐ. ǰȩȥȖȟșȖȠȪ ȥȖȟșȜ ȐȎȞȖȎțȠȜȐ ȞȎȟȝȞȓȒȓșȓțȖȭ ȝȞȖȕȜȐ, ȓȟșȖ ȝȜ ȘȎȔȒȜȗ țȜȚȖțȎȤȖȖ ȡȟȠȎțȜȐșȓțȩ: Ȏ) ȞȎȕșȖȥțȩȓ ȝȞȖȕȩ; ȏ) ȜȒȖțȎȘȜȐȩȓ ȝȞȖȕȩ.
23.ǿȘȜșȪȘȜ ȞȎȕșȖȥțȩȣ ȟșȜȐ ȚȜȔțȜ ȟȜȟȠȎȐȖȠȪ, ȝȓȞȓȟȠȎȐșȭȭ ȏȡȘȐȩ Ȑ ȟșȜȐȓ «ȚȎȚȎ»? ǰȩȝȖȟȎȠȪ Ȑȟȓ ȫȠȖ ȟșȜȐȎ.
ǾdzȆdzǻǶdz. ȅȖȟșȜ ȞȎȕșȖȥțȩȣ ȟșȜȐ, ȘȜȠȜȞȩȓ ȚȜȔțȜ ȟȜȟȠȎȐȖȠȪ, ȝȓȞȓȟȠȎȐșȭȭ ȏȡȘȐȩ Ȑ ȟșȜȐȓ «ȚȎȚȎ», ȜȝȖȟȩȐȎȓȠȟȭ ȥȖȟșȜȚ ȝȓȞȓȟȠȎțȜȐȜȘ ȟ ȝȜȐȠȜȞȓțȖȭȚȖ Ȗȕ n = 4 ȫșȓȚȓțȠȜȐ (ȏȡȘȐ Ȑ ȟșȜȐȓ «ȚȎȚȎ»), Ȑ ȘȜȠȜȞȩȓ ȝȓȞȐȩȗ ȫșȓȚȓțȠ (ȏȡȘȐȎ «Ț») ȐȣȜȒȖȠ n1 = 2 ȞȎȕȎ, Ȏ ȐȠȜȞȜȗ ȫșȓȚȓțȠ (ȏȡȘȐȎ «Ȏ») — n2 = 2 ȞȎȕȎ
(n1 + n2 = 4 = n ). ȋȠȜ ȥȖȟșȜ ȞȎȐțȜ |
% |
(2, 2) = |
|
4! |
|
6 . ȆȓȟȠȪ ȞȎȕșȖȥțȩȣ ȟșȜȐ, ȝȜșȡȥȎȬȧȖȓȟȭ ȝȓ- |
P4 |
|
|
= |
|||
|
ɑ |
|||||
|
|
2 |
!2! |
|
|
|
ȞȓȟȠȎțȜȐȘȎȚȖ ȏȡȘȐ Ȑ ȟșȜȐȓ «ȚȎȚȎ», ȠȎȘȜȐȩ: «ȚȚȎȎ», «ȚȎȚȎ», «ȚȎȎȚ», «ȎȚȚȎ», «ȎȚȎȚ», «ȎȎȚȚ».
24.ǿȘȜșȪȘȜ ȞȎȕșȖȥțȩȣ ȟșȜȐ ȚȜȔțȜ ȟȜȟȠȎȐȖȠȪ, ȝȓȞȓȟȠȎȐșȭȭ ȏȡȘȐȩ Ȑ ȟșȜȐȓ «ȚȎ-
ȠȓȚȎȠȖȘȎ»?
25.DzȜȘȎȕȎȠȪ ȟȝȞȎȐȓȒșȖȐȜȟȠȪ ȢȜȞȚȡș (1.6) – (1.8).
8
§1.2. ǶǿȅǶǿǹdzǻǶdz ǿǼǯȉȀǶǷ
ǿșȡȥȎȗțȜȓ ȟȜȏȩȠȖȓ A , ȟȐȭȕȎțțȜȓ ȟ ȜȝȩȠȜȚ S , — ȫȠȜ ȠȎȘȜȓ ȟȜȏȩȠȖȓ, ȘȜȠȜȞȜȓ ȚȜȔȓȠ ȝȞȜȖȕȜȗȠȖ ȖșȖ țȓ ȝȞȜȖȕȜȗȠȖ Ȑ ȞȓȕȡșȪȠȎȠȓ ȜȝȩȠȎ S , ȝȞȖȥȮȚ ȕȎȞȎțȓȓ, ȒȜ ȝȞȜȐȓȒȓțȖȭ ȜȝȩȠȎ, țȓȖȕȐȓȟȠțȜ, ȝȞȜȖȕȜȗȒȮȠ ȜțȜ ȖșȖ țȓȠ. ǰȟȬȒȡ Ȑ ȒȎșȪțȓȗȦȓȚ ȝȞȖ ȞȎȟȟȚȜȠȞȓțȖȖ ȟșȡȥȎȗțȩȣ ȟȜȏȩȠȖȗ Țȩ ȏȡȒȓȚ ȜȝȡȟȘȎȠȪ ȟșȜȐȜ «ȟșȡȥȎȗțȜȓ». DzȜȟȠȜȐȓȞțȩȚ ȟȜȏȩȠȖȓȚ, ȟȐȭȕȎțțȩȚ ȟ ȜȝȩȠȜȚ S , țȎȕȩȐȎȓȠȟȭ ȠȎȘȜȓ ȟȜȏȩȠȖȓ W, ȘȜ-
ȠȜȞȜȓ ȜȏȭȕȎȠȓșȪțȜ ȝȞȜȖȕȜȗȒȮȠ Ȑ ȞȓȕȡșȪȠȎȠȓ ȜȝȩȠȎ S . ǻȓȐȜȕȚȜȔțȩȚ ȟȜȏȩȠȖȓȚ, ȟȐȭȕȎțțȩȚ ȟ ȜȝȩȠȜȚ S , țȎȕȩȐȎȓȠȟȭ ȠȎȘȜȓ ȟȜȏȩȠȖȓ ɀ, ȘȜȠȜȞȜȓ ȜȏȭȕȎȠȓșȪțȜ țȓ ȝȞȜȖȕȜȗȒȮȠ Ȑ ȞȓȕȡșȪȠȎȠȓ ȜȝȩȠȎ S .
ǻȎȒ ȟȜȏȩȠȖȭȚȖ A Ȗ B , ȟȐȭȕȎțțȩȚȖ ȟ ȜȒțȖȚ Ȗ ȠȓȚ Ȕȓ ȜȝȩȠȜȚ S , ȜȝȞȓȒȓșȓțȩ ȟșȓȒȡȬȧȖȓ ȜȝȓȞȎȤȖȖ.
ǿȜȏȩȠȖȓ A ȐșȓȥȮȠ ȕȎ ȟȜȏȜȗ ȟȜȏȩȠȖȓ B (ȖșȖ ȟȜȏȩȠȖȓ A ȐșȜȔȓțȜ Ȑ ȟȜȏȩȠȖȓ B ), ȓȟșȖ ȘȎȔȒȜȓ ȝȜȭȐ-
șȓțȖȓ ȟȜȏȩȠȖȭ A ȟȜȝȞȜȐȜȔȒȎȓȠȟȭ ȝȜȭȐșȓțȖȓȚ ȟȜȏȩȠȖȭ B . ȋȠȜ ȜȏȜȕțȎȥȎȓȠȟȭ ȘȎȘ A ɇ B . ǿȜȏȩȠȖȭ A Ȗ B țȎȕȩȐȎȬȠ ȫȘȐȖȐȎșȓțȠțȩȚȖ, ȓȟșȖ A ɇ B Ȗ B ɇ A . ȋȘȐȖȐȎșȓțȠțȜȟȠȪ ȜȏȜȕțȎȥȎȓȠȟȭ ȘȎȘ A = B .
ǼȏȨȓȒȖțȓțȖȓȚ (ȖșȖ ȟȡȚȚȜȗ) ȟȜȏȩȠȖȗ A Ȗ B țȎȕȩȐȎȓȠȟȭ ȟȜȏȩȠȖȓ A ɂB (ȖșȖ A + B ), ȘȜȠȜȞȜȓ țȎȟȠȡȝȎȓȠ ȐȟȓȑȒȎ, ȘȜȑȒȎ țȎȟȠȡȝȎȓȠ șȖȏȜ ȟȜȏȩȠȖȓ A , șȖȏȜ ȟȜȏȩȠȖȓ B .
ǽȓȞȓȟȓȥȓțȖȓȚ (ȖșȖ ȝȞȜȖȕȐȓȒȓțȖȓȚ) ȟȜȏȩȠȖȗ A Ȗ B țȎȕȩȐȎȓȠȟȭ ȟȜȏȩȠȖȓ A Ɂ B (ȖșȖ AB ), ȘȜȠȜȞȜȓ țȎȟȠȡȝȎȓȠ ȐȟȓȑȒȎ, ȘȜȑȒȎ ȟȜȏȩȠȖȭ A Ȗ B țȎȟȠȡȝȎȬȠ ȜȒțȜȐȞȓȚȓțțȜ.
DzȜȝȜșțȓțȖȓȚ ȟȜȏȩȠȖȭ B ȒȜ ȟȜȏȩȠȖȭ A (ȖșȖ ȞȎȕțȜȟȠȪȬ ȟȜȏȩȠȖȗ A Ȗ B ) țȎȕȩȐȎȓȠȟȭ ȟȜȏȩȠȖȓ
A \ B , ȘȜȠȜȞȜȓ țȎȟȠȡȝȎȓȠ ȐȟȓȑȒȎ, ȘȜȑȒȎ țȎȟȠȡȝȎȓȠ ȟȜȏȩȠȖȓ A , Ȗ ȝȞȖ ȫȠȜȚ țȓ țȎȟȠȡȝȎȓȠ ȟȜȏȩȠȖȓ B .
ǽȞȜȠȖȐȜȝȜșȜȔțȩȚ ȟȜȏȩȠȖȬ A țȎȕȩȐȎȓȠȟȭ ȟȜȏȩȠȖȓ A = W\ A (ȥȖȠȎȓȠȟȭ «țȓ A »), ȘȜȠȜȞȜȓ țȎȟȠȡȝȎȓȠ ȐȟȓȑȒȎ, ȘȜȑȒȎ ȟȜȏȩȠȖȓ A țȓ țȎȟȠȡȝȎȓȠ.
ǿȜȏȩȠȖȭ A Ȗ B țȎȕȩȐȎȬȠȟȭ țȓȟȜȐȚȓȟȠțȩȚȖ, ȓȟșȖ A Ɂ B = ɀ, Ƞ. ȓ. ȓȟșȖ Ȑ ȞȓȕȡșȪȠȎȠȓ ȜȝȩȠȎ ȟȜȏȩȠȖȭ A Ȗ B țȓ ȚȜȑȡȠ țȎȟȠȡȝȖȠȪ ȜȒțȜȐȞȓȚȓțțȜ.
DZȜȐȜȞȭȠ, ȥȠȜ ȟȜȏȩȠȖȭ H1,H2,K ,Hn ȜȏȞȎȕȡȬȠ ȝȜșțȡȬ ȑȞȡȝȝȡ, ȓȟșȖ ȜțȖ ȝȜȝȎȞțȜ țȓȟȜȐȚȓȟȠțȩ
(Hi Ɂ H j = ɀ, i ʋj ) Ȗ Ȗȣ ȜȏȨȓȒȖțȓțȖȓ ȫȘȐȖȐȎșȓțȠțȜ ȒȜȟȠȜȐȓȞțȜȚȡ ȟȜȏȩȠȖȬ (H1 ɂH2 ɂ
ɂL ɂHn = W).
ǿșȡȥȎȗțȜȓ ȟȜȏȩȠȖȓ w , ȟȐȭȕȎțțȜȓ ȟ ȜȝȩȠȜȚ S , ȘȜȠȜȞȜȓ țȓȐȜȕȚȜȔțȜ ȝȞȓȒȟȠȎȐȖȠȪ ȘȎȘ ȜȏȨȓȒȖțȓțȖȓ ȖșȖ ȝȓȞȓȟȓȥȓțȖȓ ȏȜșȓȓ ȝȞȜȟȠȩȣ ȟȜȏȩȠȖȗ, ȟȐȭȕȎțțȩȣ ȟ ȠȓȚ Ȕȓ ȜȝȩȠȜȚ, țȎȕȩȐȎȓȠȟȭ ȫșȓȚȓțȠȎȞțȩȚ ȟȜȏȩȠȖȓȚ. ǼȥȓȐȖȒțȜ, ȒȜȟȠȜȐȓȞțȜȓ ȟȜȏȩȠȖȓ W= {w} — ȫȠȜ ȚțȜȔȓȟȠȐȜ Ȑȟȓȣ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ (ȝȜȫȠȜȚȡ W țȎȕȩȐȎȬȠ ȓȧȮ ȝȞȜȟȠȞȎțȟȠȐȜȚ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ), Ȏ țȓȐȜȕȚȜȔțȜȓ ȟȜȏȩȠȖȓ ɀ — ȫȠȜ ȝȡȟȠȜȓ ȚțȜȔȓȟȠȐȜ. ǹȬȏȜȓ ȟȜȏȩȠȖȓ, ȟȐȭȕȎțțȜȓ ȟ ȜȝȩȠȜȚ S , ȚȜȔțȜ ȝȞȓȒȟȠȎȐȖȠȪ ȘȎȘ țȓȘȜȠȜȞȜȓ ȝȜȒȚțȜȔȓȟȠȐȜ ȒȜȟȠȜȐȓȞțȜȑȜ ȟȜȏȩȠȖȭ W, Ƞ. ȓ. ȘȎȘ ȚțȜȔȓȟȠȐȜ țȓȘȜȠȜȞȩȣ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩ-
ȠȖȗ.
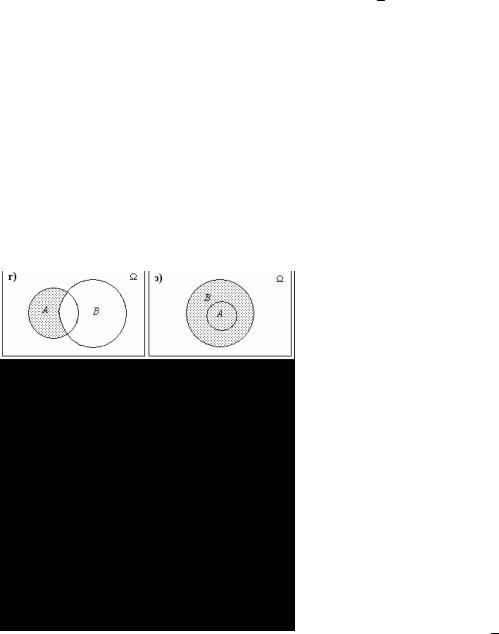
Dzșȭ țȎȑșȭȒțȜȑȜ ȝȞȓȒȟȠȎȐșȓțȖȭ ȟȜȏȩȠȖȗ, ȜȝȓȞȎȤȖȗ țȎȒ ȟȜȏȩȠȖȭȚȖ Ȗ ȜȠțȜȦȓțȖȗ ȚȓȔȒȡ țȖȚȖ ȖȟȝȜșȪȕȡȬȠȟȭ ȒȖȎȑȞȎȚȚȩ ǰȪȓțțȎ – ȋȗșȓȞȎ (ȞȖȟ. 1.1).
ǻȎ ȫȠȖȣ ȒȖȎȑȞȎȚȚȎȣ ȒȜȟȠȜȐȓȞțȜȓ ȟȜȏȩȠȖȓ W ȖȕȜȏȞȎȔȎȓȠȟȭ Ȑ ȐȖȒȓ țȓȘȜȠȜȞȜȗ ȜȏșȎȟȠȖ țȎ ȝșȜȟȘȜȟȠȖ, ȫșȓȚȓțȠȎȞțȩȓ ȟȜȏȩȠȖȭ wi — ȠȜȥȘȎȚȖ ȐțȡȠȞȖ Ȝȏ-
șȎȟȠȖ, ȟȜȜȠȐȓȠȟȠȐȡȬȧȓȗ W. ǽȞȖ ȫȠȜȚ șȬȏȜȚȡ ȟșȡ-
ȥȎȗțȜȚȡ ȟȜȏȩȠȖȬ A ȏȡȒȓȠ ȟȜȜȠȐȓȠȟȠȐȜȐȎȠȪ țȓȘȜȠȜȞȎȭ ȑȓȜȚȓȠȞȖȥȓȟȘȎȭ ȢȖȑȡȞȎ ȐțȡȠȞȖ ȜȏșȎȟȠȖ, ȟȜȜȠȐȓȠȟȠȐȡȬȧȓȗ W (ȞȖȟ. 1.1Ȏ). ǼȏȨȓȒȖțȓțȖȓ A ɂB ȟȜȏȩȠȖȗ A Ȗ B ȟȜȟȠȜȖȠ Ȗȕ Ȑȟȓȣ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ, ȝȞȖțȎȒșȓȔȎȧȖȣ, ȝȜ ȘȞȎȗțȓȗ ȚȓȞȓ, ȜȒțȜȚȡ Ȗȕ ȟȜȏȩȠȖȗ A Ȗ B (ȞȖȟ. 1.1ȏ). ǽȓȞȓȟȓȥȓțȖȓ A Ɂ B ȟȜȏȩȠȖȗ A Ȗ B ȟȜȟȠȜȖȠ Ȗȕ Ȑȟȓȣ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ, ȝȞȖțȎȒșȓȔȎȧȖȣ ȜȒțȜȐȞȓȚȓțțȜ ȜȏȜȖȚ ȟȜȏȩȠȖȭȚ A Ȗ B (ȞȖȟ. 1.1Ȑ). DzȜȝȜșțȓțȖȓ A \ B ȟȜȏȩȠȖȭ B ȒȜ ȟȜȏȩȠȖȭ A ȟȜȟȠȜȖȠ Ȗȕ Ȑȟȓȣ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ, ȝȞȖțȎȒșȓȔȎȧȖȣ ȟȜȏȩȠȖȬ A Ȗ ȝȞȖ ȫȠȜȚ țȓ ȝȞȖțȎȒșȓȔȎȧȖȣ ȟȜȏȩȠȖȬ
B (ȞȖȟ. 1.1ȑ). ǿȜȏȩȠȖȓ A , ȝȞȜȠȖȐȜȝȜșȜȔțȜȓ ȟȜȏȩ-
9
ȠȖȬ A , ȟȜȟȠȜȖȠ Ȗȕ Ȑȟȓȣ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ, țȓ ȝȞȖțȎȒșȓȔȎȧȖȣ ȟȜȏȩȠȖȬ A (ȞȖȟ. 1.1Ȓ). ǻȓȟȜȐȚȓȟȠțȩȓ ȟȜȏȩȠȖȭ țȓ ȖȚȓȬȠ ȜȏȧȖȣ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ (ȞȖȟ. 1.1ȓ). ǽȜșțȎȭ ȑȞȡȝȝȎ ȟȜȏȩȠȖȗ ȝȞȓȒȟȠȎȐșȓțȎ țȎ ȞȖȟ. 1.1Ȕ. ǿȜȏȩȠȖȓ A ȐșȓȥȮȠ ȕȎ ȟȜȏȜȗ ȟȜȏȩȠȖȓ B , ȓȟșȖ Ȑȟȓ ȫșȓȚȓțȠȎȞțȩȓ ȟȜȏȩȠȖȭ, ȐȣȜȒȭȧȖȓ Ȑ A , ȐȣȜȒȭȠ Ȗ Ȑ B (ȞȖȟ. 1.1ȕ).
ǼȝȓȞȎȤȖȖ țȎȒ ȟȜȏȩȠȖȭȚȖ ȜȏșȎȒȎȬȠ ȟșȓȒȡȬȧȖȚȖ ȟȐȜȗȟȠȐȎȚȖ:
ȘȜȚȚȡȠȎȠȖȐțȜȟȠȪ ȜȏȨȓȒȖțȓțȖȭ ȟȜȏȩȠȖȗ: |
|
|||||||||||
A ɂB = B ɂA , |
(1.9) |
|||||||||||
ȎȟȟȜȤȖȎȠȖȐțȜȟȠȪ ȜȏȨȓȒȖțȓțȖȭ ȟȜȏȩȠȖȗ: |
|
|||||||||||
(A ɂB) ɂC = A ɂ(B ɂC ) , |
(1.10) |
|||||||||||
|
A ɂA = A , |
(1.11) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A ɂA = W, |
(1.12) |
||||||||||
|
A ɂɀ= A , |
(1.13) |
||||||||||
|
A ɂW= W, |
(1.14) |
||||||||||
ȘȜȚȚȡȠȎȠȖȐțȜȟȠȪ ȝȓȞȓȟȓȥȓțȖȭ ȟȜȏȩȠȖȗ: |
|
|||||||||||
|
A Ɂ B = B Ɂ A , |
(1.15) |
||||||||||
ȎȟȟȜȤȖȎȠȖȐțȜȟȠȪ ȝȓȞȓȟȓȥȓțȖȭ ȟȜȏȩȠȖȗ: |
|
|||||||||||
(A Ɂ B) Ɂ C = A Ɂ (B Ɂ C ) , |
(1.16) |
|||||||||||
ȒȖȟȠȞȖȏȡȠȖȐțȜȟȠȪ ȝȓȞȓȟȓȥȓțȖȭ ȟȜȏȩȠȖȗ ȜȠțȜȟȖȠȓșȪțȜ ȜȏȨȓȒȖțȓțȖȭ: |
|
|||||||||||
(A ɂB) Ɂ C = (A Ɂ C ) ɂ(B Ɂ C ) , |
(1.17) |
|||||||||||
|
A Ɂ A = A , |
(1.18) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A Ɂ A = ɀ, |
(1.19) |
||||||||||
|
A Ɂ ɀ= ɀ, |
(1.20) |
||||||||||
|
A Ɂ W= A , |
(1.21) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
A \ B = A Ɂ B , |
(1.22) |
||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
W= ɀ, |
(1.23) |
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
ɀ= W, |
(1.24) |
|||||||||
ȝȞȎȐȖșȎ Ȓȓ ǺȜȞȑáțȎ: |
|
|||||||||||
|
|
|
|
|
|
|
||||||
|
A ɂB = A Ɂ B , |
(1.25) |
||||||||||
|
|
|
|
|||||||||
|
A Ɂ B = A ɂB . |
(1.26) |
||||||||||
26.ǽȞȖȐȓȟȠȖ ȝȞȖȚȓȞȩ ȝȞȜȠȖȐȜȝȜșȜȔțȩȣ ȟșȡȥȎȗțȩȣ ȟȜȏȩȠȖȗ.
27.ǽȞȖȐȓȟȠȖ ȝȞȖȚȓȞȩ țȓȟȜȐȚȓȟȠțȩȣ ȟșȡȥȎȗțȩȣ ȟȜȏȩȠȖȗ.
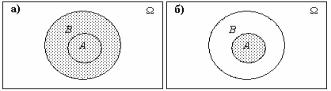
28.ǶȕȐȓȟȠțȜ, ȥȠȜ A ɇ B . ǻȎȗȠȖ: Ȏ) A ɂB ; ȏ) A Ɂ B .
ǾdzȆdzǻǶdz. ǿȜȏȩȠȖȓ A ɂB ȕȎȦȠȞȖȣȜȐȎțȜ țȎ ȞȖȟ. 1.2Ȏ, ȟȜȏȩȠȖȓ A Ɂ B — țȎ ȞȖȟ. 1.2ȏ, ȜȠȘȡȒȎ ȟșȓȒȡȓȠ, ȜȥȓȐȖȒțȜ, ȥȠȜ AɂB = B , AɁB = A .
29.ȁȟȠȎțȜȐȖȠȪ, ȝȞȖ ȘȎȘȖȣ ȡȟșȜȐȖȭȣ
ȟȜȏȩȠȖȭ A Ȗ A Ɂ B ȭȐșȭȬȠȟȭ ȫȘȐȖȐȎșȓțȠ-
țȩȚȖ. |
ǾȖȟ. 1.2. ǿȜȏȩȠȖȭ AɂB (Ȏ) Ȗ AɁB (ȏ), ȘȜȑȒȎ AɇB |
|
30.ǽȡȟȠȪ A, B, C — ȝȞȜȖȕȐȜșȪțȩȓ ȟȜȏȩȠȖȭ. ǻȎȗȠȖ ȐȩȞȎȔȓțȖȭ Ȓșȭ ȟȜȏȩȠȖȗ,
ȟȜȟȠȜȭȧȖȣ Ȑ ȠȜȚ, ȥȠȜ: Ȏ) ȝȞȜȖȕȜȦșȜ ȠȜșȪȘȜ A ; ȏ) ȝȞȜȖȕȜȦșȖ A Ȗ B , țȜ C țȓ ȝȞȜȖȕȜȦșȜ; Ȑ) Ȑȟȓ ȠȞȖ ȟȜȏȩȠȖȭ ȝȞȜȖȕȜȦșȖ; ȑ) ȝȞȜȖȕȜȦșȜ ȣȜȠȭ ȏȩ ȜȒțȜ Ȗȕ ȫȠȖȣ ȟȜȏȩȠȖȗ; Ȓ) ȝȞȜȖȕȜȦșȜ ȣȜȠȭ ȏȩ ȒȐȎ ȟȜȏȩȠȖȭ; ȓ) țȖ ȜȒțȜ Ȗȕ ȟȜȏȩȠȖȗ A , B Ȗ C țȓ ȝȞȜȖȕȜȦșȜ; Ȕ) ȝȞȜȖȕȜȦșȜ țȓ ȏȜșȓȓ ȒȐȡȣ Ȗȕ ȟȜȏȩȠȖȗ A , B Ȗ C ; ȕ) ȝȞȜȖȕȜȦșȜ ȞȜȐțȜ ȜȒțȜ Ȗȕ ȫȠȖȣ ȟȜȏȩȠȖȗ; Ȗ) ȝȞȜȖȕȜȦșȜ ȞȜȐțȜ ȒȐȎ Ȗȕ ȫȠȖȣ ȟȜȏȩȠȖȗ.
10

31.ǽȡȟȠȪ A, B, C — țȓȘȜȠȜȞȩȓ ȟȜȏȩȠȖȭ, ȝȞȖȥȮȚ A ɇ B . ǿ ȝȜȚȜȧȪȬ ȒȖȎ-
ȑȞȎȚȚ ǰȪȓțțȎ – ȋȗșȓȞȎ ȡȝȞȜȟȠȖȠȪ ȐȩȞȎȔȓțȖȭ: Ȏ) A Ɂ B ; ȏ) A ɂB ; Ȑ) A Ɂ B Ɂ C ;
ȑ) A ɂB ɂC .
32.ǽȞȜȐȓȞȖȠȪ ȟȝȞȎȐȓȒșȖȐȜȟȠȪ ȟșȓȒȡȬȧȖȣ ȡȠȐȓȞȔȒȓțȖȗ, ȟȞȎȐțȖȐȎȭ ȒȖȎȑȞȎȚ-
Țȩ ǰȪȓțțȎ – ȋȗșȓȞȎ |
Ȓșȭ ȟȜȏȩȠȖȗ, ȟȠȜȭȧȖȣ Ȑ șȓȐȩȣ Ȗ Ȑ ȝȞȎȐȩȣ ȥȎȟȠȭȣ: |
Ȏ) (AɂB)\C = Aɂ(B\C ); |
ȏ) A Ɂ B Ɂ C = A Ɂ B Ɂ (C ɂB); Ȑ) AɂBɂC = Aɂ(B\(AɁB))ɂ |
ɂ(C \(AɁC )) ; ȑ) A ɂB = (A\(A Ɂ B)) ɂB ; Ȓ) (A ɂB)\ A = B ; ȓ) (A ɂB ɂC ) = A Ɂ B ɁC ;
Ȕ) (A ɂB)ɁC = (A ɁC )ɂ(B ɁC ); ȕ) (A ɂB) ɁC = A Ɂ B ɁC ; Ȗ) (AɂB)ɁC = C\(C Ɂ(AɂB)) ;
Ș) A Ɂ B ɁC ɇ(B ɁC )ɂ(C Ɂ A) ; ș) (AɁB)ɂ(B ɁC )ɂ(C ɁA)ɇA ɂB ɂC ; Ț) AɁB ɁC ɇAɂB .
33.ǿ ȝȜȚȜȧȪȬ ȒȖȎȑȞȎȚȚ ǰȪȓțțȎ – ȋȗșȓȞȎ ȡȏȓȒȖȠȪȟȭ Ȑ ȟȝȞȎȐȓȒșȖȐȜȟȠȖ ȟȐȜȗȟȠȐ (1.9) – (1.26) Ȓșȭ ȝȞȜȖȕȐȜșȪțȩȣ ȟȜȏȩȠȖȗ A, B, C .
34.ǽȞȜȐȓȞȖȠȪ, ȭȐșȭȬȠȟȭ șȖ ȟȜȏȩȠȖȭ A Ȗ A ɂB (ȑȒȓ A Ȗ B — ȝȞȜȖȕȐȜșȪțȩȓ ȟȜȏȩȠȖȭ) țȓȟȜȐȚȓȟȠțȩȚȖ.
ǾdzȆdzǻǶdz. A Ɂ (A ɂB) = {ȝȜ ȝȞȎȐȖșȡ Ȓȓ ǺȜȞȑáțȎ}= A Ɂ (A Ɂ B) = {ȝȜ ȟȐȜȗȟȠȐȡ ȎȟȟȜȤȖȎȠȖȐțȜȟȠȖ
ȝȓȞȓȟȓȥȓțȖȭ}= (A Ɂ A) Ɂ B = ɒɁ B = ɒ, ȕțȎȥȖȠ, ȟȜȏȩȠȖȭ A Ȗ A ɂB ȭȐșȭȬȠȟȭ țȓȟȜȐȚȓȟȠțȩȚȖ.
35. ǽȞȜȐȓȞȖȠȪ, |
ȜȏȞȎȕȡȬȠ șȖ ȟȜȏȩȠȖȭ A , A Ɂ B , A ɂB ȝȜșțȡȬ ȑȞȡȝȝȡ (A Ȗ |
B — ȝȞȜȖȕȐȜșȪțȩȓ ȟȜȏȩȠȖȭ). |
|
§1.3. |
ǸǹǮǿǿǶȅdzǿǸǼdz ǼǽǾdzDzdzǹdzǻǶdz ǰdzǾǼȍȀǻǼǿȀǶ |
ǰȓȞȜȭȠțȜȟȠȪ țȎȟȠȡȝșȓțȖȭ ȟȜȏȩȠȖȭ ȣȎȞȎȘȠȓȞȖȕȡȓȠ ȚȓȞȡ ȐȜȕȚȜȔțȜȟȠȖ țȎȟȠȡȝșȓțȖȭ ȫȠȜȑȜ ȟȜȏȩȠȖȭ ȝȞȖ ȝȞȜȐȓȒȓțȖȖ ȜȝȩȠȎ. dzȟșȖ ȚțȜȔȓȟȠȐȜ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ W= {w1, w2,..., wN } ȘȜțȓȥțȜ, Ȗ
Ȑȟȓ ȫșȓȚȓțȠȎȞțȩȓ ȟȜȏȩȠȖȭ ȜȒȖțȎȘȜȐȜ ȐȜȕȚȜȔțȩ, ȠȜ ȠȎȘȎȭ ȐȓȞȜȭȠțȜȟȠțȎȭ ȟȣȓȚȎ țȜȟȖȠ țȎȕȐȎțȖȓ
ȘșȎȟȟȖȥȓȟȘȜȗ. ǰ ȫȠȜȚ ȟșȡȥȎȓ ȐȓȞȜȭȠțȜȟȠȪ P{A} țȎȟȠȡȝșȓțȖȭ ȟȜȏȩȠȖȭ A , ȟȜȟȠȜȭȧȓȑȜ Ȗȕ M ȫșȓȚȓț-
ȠȎȞțȩȣ ȟȜȏȩȠȖȗ, ȐȣȜȒȭȧȖȣ Ȑ W, ȜȝȞȓȒȓșȭȓȠȟȭ ȘȎȘ ȜȠțȜȦȓțȖȓ ȥȖȟșȎ M ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ,
ȏșȎȑȜȝȞȖȭȠȟȠȐȡȬȧȖȣ țȎȟȠȡȝșȓțȖȬ ȟȜȏȩȠȖȭ A , Ș ȜȏȧȓȚȡ ȥȖȟșȡ N |
ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ. ȋȠȎ |
|||||||||
ȢȜȞȚȡșȎ țȜȟȖȠ țȎȕȐȎțȖȓ ȘșȎȟȟȖȥȓȟȘȜȑȜ ȜȝȞȓȒȓșȓțȖȭ ȐȓȞȜȭȠțȜȟȠȖ: |
|
|||||||||
|
P{A} = |
M |
. |
(1.27) |
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
N |
|
||
ǰ ȥȎȟȠțȜȟȠȖ, ȟȜȑșȎȟțȜ ȘșȎȟȟȖȥȓȟȘȜȚȡ ȜȝȞȓȒȓșȓțȖȬ ȐȓȞȜȭȠțȜȟȠȖ, |
|
|||||||||
P{w } = |
1 |
, i = 1, 2,...,N , |
(1.28) |
|||||||
|
||||||||||
i |
|
N |
|
|||||||
|
|
|
||||||||
|
P{W} = |
|
N |
= 1 , |
(1.29) |
|||||
|
|
|
||||||||
|
|
|
|
|
N |
|
||||
|
P{ɀ} = |
0 |
= 0 . |
(1.30) |
||||||
|
|
|||||||||
|
|
|
|
|
N |
|
||||
ȅȎȟȠțȩȚ ȟșȡȥȎȓȚ ȘșȎȟȟȖȥȓȟȘȜȗ ȐȓȞȜȭȠțȜȟȠțȜȗ ȟȣȓȚȩ ȭȐșȭȓȠȟȭ ȡȞțȜȐȎȭ ȟȣȓȚȎ: Ȑ ȡȞțȓ ȟȜȒȓȞȔȖȠȟȭ (K + L) ȦȎȞȜȐ, ȟȞȓȒȖ ȘȜȠȜȞȩȣ K ȏȓșȩȣ Ȗ L ȥȮȞțȩȣ; Ȗȕ ȡȞțȩ țȎȡȑȎȒ ȏȓȕ ȐȜȕȐȞȎȧȓțȖȭ ȖȕȐșȓȘȎȬȠȟȭ (k + l) ȦȎȞȜȐ, ȠȜȑȒȎ ȐȓȞȜȭȠțȜȟȠȪ PK ,L (k,l) ȠȜȑȜ, ȥȠȜ Ȑ ȐȩȏȜȞȘȓ ȟȜȒȓȞȔȖȠȟȭ ȞȜȐțȜ k ȏȓșȩȣ ȦȎ-
ȞȜȐ Ȗ l ȥȮȞțȩȣ, ȐȩȥȖȟșȭȓȠȟȭ ȝȜ ȢȜȞȚȡșȓ ȑȖȝȓȞȑȓȜȚȓȠȞȖȥȓȟȘȜȗ ȐȓȞȜȭȠțȜȟȠȖ:
P |
(k,l) = |
CkK ClL |
. |
(1.31) |
|
||||
K ,L |
|
Ck+ l |
|
|
|
|
K + L |
|
|
ǰ ȟșȡȥȎȓ, ȘȜȑȒȎ ȚțȜȔȓȟȠȐȜ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ ȏȓȟȘȜțȓȥțȜ Ȗ ȒȎȔȓ țȓȟȥȮȠțȜ (țȜ ȫȠȖ ȟȜȏȩȠȖȭ ȭȐșȭȬȠȟȭ ȜȒȖțȎȘȜȐȜ ȐȜȕȚȜȔțȩȚȖ), ȐȓȞȜȭȠțȜȟȠȪ țȎȟȠȡȝșȓțȖȭ ȟȜȏȩȠȖȭ ȚȜȔțȜ ȞȎȟȟȥȖȠȎȠȪ, ȝȜșȪȕȡȭȟȪ ȑȓȜȚȓȠȞȖȥȓȟȘȖȚ ȜȝȞȓȒȓșȓțȖȓȚ ȐȓȞȜȭȠțȜȟȠȖ, ȘȜȠȜȞȜȓ ȟȜȟȠȜȖȠ Ȑ ȟșȓȒȡȬȧȓȚ. ǽȡȟȠȪ ȚțȜȔȓȟȠȐȜ
11

ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ W ȝȞȓȒȟȠȎȐșȭȓȠ ȟȜȏȜȗ țȓȘȜȠȜȞȡȬ ȜȏșȎȟȠȪ Ȑ d -ȚȓȞțȜȚ ȝȞȜȟȠȞȎțȟȠȐȓ,
ȖȚȓȬȧȡȬ țȓțȡșȓȐȜȗ ȜȏȨȮȚ1 V (W) : Wɇ ȸd, 0 < V (W) < ʈ . ǽȞȖ ȫȠȜȚ ȘȎȔȒȜȚȡ ȫșȓȚȓțȠȎȞțȜȚȡ ȟȜ-
ȏȩȠȖȬ ȟȜȜȠȐȓȠȟȠȐȡȓȠ ȠȜȥȘȎ w ɈWɇ ȸd , Ȏ ȘȎȔȒȜȓ ȟȜȏȩȠȖȓ A ȝȞȓȒȟȠȎȐșȭȓȠ ȟȜȏȜȗ ȜȏșȎȟȠȪ, ȐșȜȔȓț-
țȡȬ Ȑ W Ȗ ȖȚȓȬȧȡȬ ȜȏȨȮȚ V (A) : A ɇ Wɇ ȸd, 0 „ V (A) < ʈ . ȀȜȑȒȎ, ȟȜȑșȎȟțȜ ȑȓȜȚȓȠȞȖȥȓȟȘȜȚȡ
ȜȝȞȓȒȓșȓțȖȬ ȐȓȞȜȭȠțȜȟȠȖ, ȐȓȞȜȭȠțȜȟȠȪ P{A} țȎȟȠȡȝșȓțȖȭ ȟȜȏȩȠȖȭ A |
ȚȜȔțȜ ȞȎȟȟȥȖȠȎȠȪ ȘȎȘ ȜȠ- |
||
țȜȦȓțȖȓ ȜȏȨȮȚȎ V (A) ȜȏșȎȟȠȖ A Ș ȜȏȨȮȚȡ V (W) ȜȏșȎȟȠȖ W: |
|
||
P{A} = |
V (A) |
. |
(1.32) |
|
|||
V (W) |
|
||
dzȟșȖ ȫșȓȚȓțȠȎȞțȩȓ ȟȜȏȩȠȖȭ țȓ ȭȐșȭȬȠȟȭ ȜȒȖțȎȘȜȐȜ ȐȜȕȚȜȔțȩȚȖ, Ȓșȭ ȝȞȖȏșȖȔȮțțȜȑȜ ȐȩȥȖȟșȓțȖȭ ȐȓȞȜȭȠțȜȟȠȓȗ ȚȜȔțȜ ȖȟȝȜșȪȕȜȐȎȠȪ ȜȠțȜȟȖȠȓșȪțȩȓ ȥȎȟȠȜȠȩ. ǽȡȟȠȪ Ȑ ȞȓȕȡșȪȠȎȠȓ n -ȘȞȎȠțȜȑȜ
ȝȞȜȐȓȒȓțȖȭ ȜȝȩȠȎ S ȟȜȏȩȠȖȓ A țȎȟȠȡȝȖșȜ mn |
ȞȎȕ. ǻȎȕȜȐȮȚ ȜȠțȜȟȖȠȓșȪțȜȗ ȥȎȟȠȜȠȜȗ p€(A) ȝȜȭȐșȓ- |
|||||||
țȖȭ ȟȜȏȩȠȖȭ A Ȑ ȟȓȞȖȖ Ȗȕ n ȜȝȩȠȜȐ S ȜȠțȜȦȓțȖȓ ȥȖȟșȎ mn |
țȎȟȠȡȝșȓțȖȗ ȟȜȏȩȠȖȭ A Ș ȜȏȧȓȚȡ |
|||||||
ȥȖȟșȡ n ȝȞȜȐȓȒȮțțȩȣ ȜȝȩȠȜȐ: |
|
|
|
|
|
|
|
|
|
|
p€(A) = |
|
mn |
. |
(1.33) |
||
|
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
ǽȞȖ ȫȠȜȚ ȐȓȞȜȭȠțȜȟȠȪ P{A} țȎȟȠȡȝșȓțȖȭ ȟȜȏȩȠȖȭ A ȏȡȒȓȠ ȞȎȐțȎ ȝȞȓȒȓșȡ2 ȜȠțȜȟȖȠȓșȪțȜȗ ȥȎȟ- |
||||||||
ȠȜȠȩ țȎȟȠȡȝșȓțȖȭ ȫȠȜȑȜ ȟȜȏȩȠȖȭ Ȑ ȟȓȞȖȖ Ȗȕ n |
ȜȝȩȠȜȐ ȝȞȖ țȓȜȑȞȎțȖȥȓțțȜȚ ȡȐȓșȖȥȓțȖȖ ȥȖȟșȎ |
|||||||
ȜȝȩȠȜȐ: |
|
|
|
|
|
|
|
|
|
mn |
|
|
P |
ɾ ® P{A} |
(1.34) |
||
|
|
ɾ |
ɾ |
ɾ |
||||
|
n |
|
n® ʈ |
|
|
|
|
|
(ȕȒȓȟȪ « ɾ ɾP ɾ® » ȜȕțȎȥȎȓȠ «ȟȣȜȒȖȠȟȭ ȝȜ ȐȓȞȜȭȠțȜȟȠȖ», ȟȚ. §4.2).
ǻȎ ȝȞȎȘȠȖȘȓ Ȑ ȫȠȜȚ ȟșȡȥȎȓ ȐȓȞȜȭȠțȜȟȠȪ ȞȎȟȟȥȖȠȩȐȎȬȠ ȝȞȖ ȝȜȚȜȧȖ ȝȞȖȏșȖȔȮțțȜȑȜ ȞȎȐȓțȟȠȐȎ
P{A} » p€(A) = |
mn |
. |
(1.35) |
n
ǿșȓȒȡȓȠ ȝȜȚțȖȠȪ, ȥȠȜ ȒȎțțȜȗ ȢȜȞȚȡșȜȗ ȚȜȔțȜ ȝȜșȪȕȜȐȎȠȪȟȭ șȖȦȪ ȝȞȖ ȐȩȝȜșțȓțȖȖ ȠȞȮȣ ȡȟșȜȐȖȗ:
xȞȎȟȟȚȎȠȞȖȐȎȓȚȩȓ ȟȜȏȩȠȖȭ ȒȜșȔțȩ ȏȩȠȪ ȖȟȣȜȒȎȚȖ ȠȜșȪȘȜ ȠȎȘȖȣ ȜȝȩȠȜȐ, ȘȜȠȜȞȩȓ ȚȜȑȡȠ ȏȩȠȪ ȐȜȟȝȞȜȖȕȐȓȒȓțȩ țȓȜȑȞȎțȖȥȓțțȜȓ ȥȖȟșȜ ȞȎȕ ȝȞȖ ȜȒțȜȚ Ȗ ȠȜȚ Ȕȓ ȘȜȚȝșȓȘȟȓ ȡȟșȜȐȖȗ;
xȟȜȏȩȠȖȭ ȒȜșȔțȩ ȜȏșȎȒȎȠȪ ȡȟȠȜȗȥȖȐȜȟȠȪȬ ȜȠțȜȟȖȠȓșȪțȩȣ ȥȎȟȠȜȠ (ȟȚ. ȠȓȜȞȓȚȡ ǯȓȞțȡșșȖ Ȑ §4.3);
xȥȖȟșȜ ȖȟȝȩȠȎțȖȗ, ȝȜ ȞȓȕȡșȪȠȎȠȎȚ ȘȜȠȜȞȩȣ ȐȩȥȖȟșȭȓȠȟȭ ȐȓȞȜȭȠțȜȟȠȪ, ȒȜșȔțȜ ȏȩȠȪ ȒȜȟȠȎȠȜȥțȜ ȐȓșȖȘȜ.
36. ǰ ȘȜȞȕȖțȓ ȠȞȖ ȘȞȎȟțȩȣ Ȗ ȟȓȚȪ ȕȓșȮțȩȣ ȭȏșȜȘ. Ƕȕ ȘȜȞȕȖțȩ ȐȩțȖȚȎȬȠ ȜȒțȜ ȭȏșȜȘȜ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ȜțȜ ȏȡȒȓȠ ȘȞȎȟțȩȚ.
ǾdzȆdzǻǶdz. ǽȡȟȠȪ ȜȝȩȠȜȚ ȏȡȒȓȠ ȖȕȐșȓȥȓțȖȓ ȭȏșȜȘȎ Ȗȕ ȘȜȞȕȖțȩ, Ȏ ȟȜȏȩȠȖȓ A ȟȜȟȠȜȖȠ Ȑ ȠȜȚ, ȥȠȜ ȖȕȐșȓȥȮțțȜȓ Ȗȕ ȘȜȞȕȖțȩ ȭȏșȜȘȜ ȜȘȎȔȓȠȟȭ ȘȞȎȟțȩȚ. ȀȜȑȒȎ Ȝȏȧȓȓ ȥȖȟșȜ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ n = 10 , Ȗȕ ȘȜȠȜȞȩȣ m = 3 ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȭ ȏșȎȑȜȝȞȖȭȠȟȠȐȡȬȠ țȎȟȠȡȝșȓțȖȬ ȟȜȏȩȠȖȭ A .
ǿȜȑșȎȟțȜ ȘșȎȟȟȖȥȓȟȘȜȚȡ ȜȝȞȓȒȓșȓțȖȬ ȐȓȞȜȭȠțȜȟȠȖ P{A} = |
m |
= |
3 |
= 0, 3. |
|
10 |
|||
|
n |
|
||
37.ǰ ȘȜȞȕȖțȓ ȠȞȖ ȘȞȎȟțȩȣ Ȗ ȟȓȚȪ ȕȓșȮțȩȣ ȭȏșȜȘ. Ƕȕ ȘȜȞȕȖțȩ ȐȩțȡșȖ ȜȒțȜ ȭȏșȜȘȜ Ȗ ȜȠșȜȔȖșȖ Ȑ ȟȠȜȞȜțȡ. ȋȠȜ ȭȏșȜȘȜ ȜȘȎȕȎșȜȟȪ ȕȓșȮțȩȚ. ǽȜȟșȓ ȫȠȜȑȜ Ȗȕ ȘȜȞȕȖțȩ ȏȓȞȡȠ ȓȧȮ ȜȒțȜ ȭȏșȜȘȜ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ȜțȜ ȏȡȒȓȠ ȘȞȎȟțȩȚ.
38.ȀȞȜȓ ȖȑȞȎȬȠ Ȑ ȘȎȞȠȩ. ǸȎȔȒȜȚȡ ȖȑȞȜȘȡ ȟȒȎțȜ ȝȜ ȒȓȟȭȠȪ ȘȎȞȠ Ȗ ȒȐȓ ȜȟȠȎȐșȓțȩ Ȑ ȝȞȖȘȡȝȓ3. ǼȒȖț Ȗȕ ȖȑȞȜȘȜȐ ȐȖȒȖȠ, ȥȠȜ ȡ țȓȑȜ țȎ ȞȡȘȎȣ ȦȓȟȠȪ ȘȎȞȠ ȏȡȏțȜȐȜȗ ȚȎȟȠȖ, Ȏ ȥȓȠȩȞȓ — ȒȞȡȑȖȣ ȚȎȟȠȓȗ. Ǽț ȟȏȞȎȟȩȐȎȓȠ ȒȐȓ ȘȎȞȠȩ Ȗȕ ȫȠȖȣ ȥȓȠȩȞȮȣ Ȗ ȏȓ-
1 ǵȒȓȟȪ ȝȜȒ ȜȏȨȮȚȜȚ V (A) ȜȏșȎȟȠȖ A ȝȜțȖȚȎȓȠȟȭ ȓȮ ȒșȖțȎ Ȑ ȜȒțȜȚȓȞțȜȚ ȟșȡȥȎȓ (d = 1), ȝșȜȧȎȒȪ Ȑ ȒȐȡȚȓȞțȜȚ ȟșȡȥȎȓ (d = 2 ), ȜȏȨȮȚ — Ȑ ȠȞȮȣȚȓȞțȜȚ ȟșȡȥȎȓ (d = 3 ) Ȗ Ƞ. Ȓ.
2 ȼ ɧɟɤɨɬɨɪɨɦ ɫɦɵɫɥɟ ɫɯɨɞɢɦɨɫɬɢ ɩɨ ɜɟɪɨɹɬɧɨɫɬɢ, ɤɨɬɨɪɵɣ ɛɭɞɟɬ ɩɨɹɫɧɺɧ ɧɢɠɟ, §4.2-§4.3.
3 ǶȚȓȓȠȟȭ Ȑ ȐȖȒȡ ȖȑȞȎ Ȑ ȝȞȓȢȓȞȎțȟ, ȘȜȑȒȎ Ȑ ȘȜșȜȒȓ ȐȟȓȑȜ 32 ȘȎȞȠȩ, ȝȜ 8 ȘȎȔȒȜȗ ȚȎȟȠȖ.
12
ȞȮȠ ȟȓȏȓ ȝȞȖȘȡȝ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ Ȑ ȝȞȖȘȡȝȓ ȜȘȎȔȡȠȟȭ ȒȐȓ ȏȡȏțȜȐȩȓ ȘȎȞȠȩ.
ǾdzȆdzǻǶdz. ǽȡȟȠȪ ȟȜȏȩȠȖȓ A ȟȜȟȠȜȖȠ Ȑ ȠȜȚ, ȥȠȜ Ȑ ȝȞȖȘȡȝȓ ȜȘȎȔȡȠȟȭ ȒȐȓ ȏȡȏțȜȐȩȓ ȘȎȞȠȩ. Ƕȕ 32 ȘȎȞȠ ȖȑȞȜȘȡ ȖȕȐȓȟȠțȩ ȒȓȟȭȠȪ, Ȏ ȜȟȠȎșȪțȩȓ 22 țȓȖȕȐȓȟȠțȩ. ǰȕȭȠȪ ȒȐȓ ȘȎȞȠȩ Ȗȕ ȝȞȖȘȡȝȎ — ȫȠȜ ȠȜ Ȕȓ ȟȎȚȜȓ, ȥȠȜ ȐȕȭȠȪ Ȗȣ Ȗȕ 22 țȓȖȕȐȓȟȠțȩȣ ȘȎȞȠ, ȟȞȓȒȖ ȘȜȠȜȞȩȣ ȒȐȓ ȏȡȏțȜȐȩȓ. ǽȜȫȠȜȚȡ Ȝȏȧȓȓ ȥȖȟșȜ
ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ n = C222 , Ȗȕ ȘȜȠȜȞȩȣ șȖȦȪ m = 1 ȫșȓȚȓțȠȎȞțȜȓ ȟȜȏȩȠȖȓ ȏșȎȑȜȝȞȖȭȠȟȠȐȡȓȠ
țȎȟȠȡȝșȓțȖȬ |
|
ȟȜȏȩȠȖȭ |
A . |
ǿȜȑșȎȟțȜ |
ȘșȎȟȟȖȥȓȟȘȜȚȡ |
ȜȝȞȓȒȓșȓțȖȬ |
ȐȓȞȜȭȠțȜȟȠȖ, |
|||||
P{A} = |
m |
= |
|
1 |
= |
1 |
. |
|
|
|
|
|
|
n C2 |
231 |
|
|
|
|
|
|
||||
|
|
|
|
22 |
|
|
|
|
|
|
|
|
39. ǰ ȝȎȞȠȖȖ, ȟȜȟȠȜȭȧȓȗ Ȗȕ 1 000 ȖȕȒȓșȖȗ, ȥȓȠȩȞȓ ȖȕȒȓșȖȭ ȖȚȓȬȠ ȒȓȢȓȘȠȩ. Dzșȭ ȘȜțȠȞȜșȭ ȜȠȏȖȞȎȬȠȟȭ 100 ȖȕȒȓșȖȗ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ȟȞȓȒȖ ȜȠȜȏȞȎțțȩȣ ȖȕȒȓșȖȗ țȓ ȜȘȎȔȓȠȟȭ ȏȞȎȘȜȐȎțțȩȣ.
|
ǾdzȆdzǻǶdz. |
|
ǽȜ |
ȢȜȞȚȡșȓ ȑȖȝȓȞȑȓȜȚȓȠȞȖȥȓȟȘȜȗ ȐȓȞȜȭȠțȜȟȠȖ |
|
|
|
|
C0C100 |
|
|||||||||||||
|
|
|
(1.31) P |
(100, 0) = |
4 996 |
= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000,4 |
C100 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
4! ɑ 996! |
|
|
|
|
4! ɑ 996! |
|
996!ɑ100!ɑ900ɑ899ɑ898ɑ897ɑ896! |
|
|
899ɑ449ɑ897 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ɑ |
|
|
|
|
|
|
|
|
|
||||
= |
0!4! 100!896 |
! |
= |
|
1 4! 100!896! |
= |
|
|
= |
|
|
|
» 0, 656 . |
|
|||||||||
|
100!ɑ896!ɑ1000ɑ999ɑ998ɑ997ɑ996! |
|
10ɑ111ɑ499ɑ997 |
|
|||||||||||||||||||
|
|
1000! |
|
|
|
|
1000ɑ999ɑ998ɑ997ɑ996! |
|
|
|
|
|
|
||||||||||
|
100!900! |
|
|
100!ɑ900ɑ899ɑ898ɑ897ɑ896! |
|
|
|
|
|
|
|
|
|
|
|||||||||
40.DzȜȘȎȕȎȠȪ ȢȜȞȚȡșȡ ȑȖȝȓȞȑȓȜȚȓȠȞȖȥȓȟȘȜȗ ȐȓȞȜȭȠțȜȟȠȖ (1.31).
41.ǰ 80-ȓ ȑȑ. XX Ȑ. Ȑ ǿǿǿǾ ȏȩșȎ ȝȜȝȡșȭȞțȎ ȖȑȞȎ «ǿȝȜȞȠșȜȠȜ». ǶȑȞȎȬȧȖȗ ȜȠȚȓȥȎș țȎ ȘȎȞȠȜȥȘȓ ȝȭȠȪ ȥȖȟȓș ȜȠ 1 ȒȜ 36 Ȗ ȝȜșȡȥȎș ȝȞȖȕȩ ȞȎȕșȖȥțȜȑȜ ȒȜȟȠȜȖțȟȠȐȎ, ȓȟșȖ Ȝț ȡȑȎȒȎș ȜȒțȜ, ȒȐȎ, ȠȞȖ, ȥȓȠȩȞȓ Ȗ ȝȭȠȪ ȥȖȟȓș, ȜȏȨȭȐșȓțțȩȣ ȠȖȞȎȔțȜȗ ȘȜȚȖȟȟȖȓȗ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȖ ȟșȓȒȡȬȧȖȣ ȟȜȏȩȠȖȗ: țȓ ȡȑȎȒȎȠȪ țȖ ȜȒțȜȑȜ ȥȖȟșȎ Ȗȕ 36, ȡȑȎȒȎȠȪ ȜȒțȜ, ȒȐȎ, ȠȞȖ, ȥȓȠȩȞȓ Ȗ ȝȭȠȪ ȥȖȟȓș Ȗȕ 36.
42.ǻȎ ȚȎșȜȚ ȝȞȓȒȝȞȖȭȠȖȖ ȞȎȏȜȠȎȬȠ ȒȓȟȭȠȪ ȟȓȚȓȗțȩȣ ȝȎȞ. ȅȠȜȏȩ țȖȘȜȚȡ țȓ ȏȩșȜ ȜȏȖȒțȜ, țȎ ȓȔȓȑȜȒțȜȚ ȟȜȏȞȎțȖȖ ȎȘȤȖȜțȓȞȜȐ ȟȜȐȓȠ ȒȖȞȓȘȠȜȞȜȐ, ȟȜȟȠȜȭȧȖȗ Ȗȕ ȐȜȟȪȚȖ ȥȓșȜȐȓȘ, ȐȩȏȖȞȎȓȠȟȭ ȟșȡȥȎȗțȩȚ ȜȏȞȎȕȜȚ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȖ ȟșȓȒȡȬȧȖȣ ȟȜȏȩȠȖȗ: Ȏ) Ȑ ȟȜȐȓȠȓ ȒȖȞȓȘȠȜȞȜȐ ȜȠȟȡȠȟȠȐȡȬȠ ȟȓȚȓȗțȩȓ ȝȎȞȩ; ȏ) Ȑ ȟȜȐȓȠȓ ȒȖȞȓȘȠȜȞȜȐ ȓȟȠȪ ȞȜȐțȜ ȜȒțȎ ȟȓȚȓȗțȎȭ ȝȎȞȎ; Ȑ) Ȑ ȟȜȐȓȠȓ ȒȖȞȓȘȠȜȞȜȐ ȓȟȠȪ ȞȜȐțȜ ȒȐȓ ȟȓȚȓȗțȩȣ ȝȎȞȩ?
43.ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ȝȞȖ ȞȎȕȒȎȥȓ ȘȜșȜȒȩ Ȑ 52 ȘȎȞȠȩ ȥȓȠȩȞȮȚ ȖȑȞȜȘȎȚ ȝȓȞȐȩȗ Ȗȕ țȖȣ ȝȜșȡȥȖȠ ȞȜȐțȜ n ȝȎȞ «Ƞȡȕ Ȗ ȘȜȞȜșȪ ȜȒțȜȗ ȚȎȟȠȖ» (n = 0, 1, 2, 3, 4).
44.DzȐȓȞȖ șȖȢȠȎ ȕȎȘȞȩșȖȟȪ țȎ ȝȓȞȐȜȚ ȫȠȎȔȓ ȝȞȭȚȜ ȝȓȞȓȒ ǽȓȠȓȗ, ȘȜȠȜȞȩȗ ȡȟȝȓș ȠȜșȪȘȜ ȕȎȚȓȠȖȠȪ, ȥȠȜ Ȑ șȖȢȠ ȐȜȦșȖ ȦȓȟȠȪ ȥȓșȜȐȓȘ. ǰ ȜȏȧȓȔȖȠȖȖ ȟȓȚȪ ȫȠȎȔȓȗ,
ȖșȖȢȠ, ȓȟșȖ ȜȠȘȞȜȓȠ țȎ ȘȎȘȜȚ-șȖȏȜ Ȗȕ țȖȣ ȒȐȓȞȖ, ȟȠȜȖȠ ȠȎȚ ȤȓșȡȬ ȚȖțȡȠȡ. ǽȓȠȭ ȔȖȐȮȠ țȎ ȟȓȒȪȚȜȚ ȫȠȎȔȓ Ȗ ȜȥȓțȪ țȓ ȣȜȥȓȠ ȖȒȠȖ ȝȜ șȓȟȠțȖȤȓ. Ǽț ȞȎȕȚȩȦșȭȓȠ, ȘȎȘȜȐȩ ȐȓȞȜȭȠțȜȟȠȖ ȟșȓȒȡȬȧȖȣ ȟȜȏȩȠȖȗ: Ȏ) Ȑȟȓ ȦȓȟȠȓȞȜ ȐȩȗȒȡȠ țȎ ȜȒțȜȚ ȫȠȎȔȓ; ȏ) Ȑȟȓ ȦȓȟȠȓȞȜ ȐȩȗȒȡȠ țȎ ȞȎȕțȩȣ ȫȠȎȔȎȣ. ǻȎȗȠȖ ȫȠȖ ȐȓȞȜȭȠțȜȟȠȖ.
ǾdzȆdzǻǶdz. Ȏ) ǼȝȩȠ, ȕȎ ȘȜȠȜȞȩȚ țȎȏșȬȒȎȓȠ ǽȓȠȭ, ȟȜȟȠȜȖȠ Ȑ ȠȜȚ, ȥȠȜ șȬȒȖ ȐȩȣȜȒȭȠ Ȗȕ șȖȢȠȎ ȝȞȜȖȕȐȜșȪțȩȚ ȜȏȞȎȕȜȚ: ȘȎȔȒȩȗ Ȗȕ ȦȓȟȠȖ ȥȓșȜȐȓȘ ȚȜȔȓȠ ȐȩȗȠȖ țȎ șȬȏȜȚ Ȗȕ ȦȓȟȠȖ ȫȠȎȔȓȗ (ȟȜ
°6 |
= |
6 |
6 |
(ȝȓȞȐȩȗ ȥȓșȜȐȓȘ ȚȜȔȓȠ Ȑȩȗ- |
ȐȠȜȞȜȑȜ ȝȜ ȟȓȒȪȚȜȗ). Ǽȏȧȓȓ ȥȖȟșȜ ȖȟȣȜȒȜȐ ȫȠȜȑȜ ȜȝȩȠȎ n = A6 |
|
ȠȖ țȎ șȬȏȜȚ Ȗȕ ȦȓȟȠȖ ȫȠȎȔȓȗ, ȐȠȜȞȜȗ — ȠȎȘȔȓ țȎ șȬȏȜȚ Ȗȕ ȦȓȟȠȖ ȫȠȎȔȓȗ Ȗ ȠȎȘ ȒȜ ȦȓȟȠȜȑȜ ȥȓșȜȐȓȘȎ; Ȑȟȓ ȫȠȖ ȦȓȟȠȪ ȦȓȟȠȮȞȜȘ ȝȓȞȓȚțȜȔȎȬȠȟȭ ȝȜ ȝȞȎȐȖșȡ ȝȞȜȖȕȐȓȒȓțȖȭ). ǽȡȟȠȪ ȟȜȏȩȠȖȓ A ȟȜȟȠȜȖȠ Ȑ ȠȜȚ, ȥȠȜ Ȑȟȓ ȦȓȟȠȪ ȥȓșȜȐȓȘ ȐȩȗȒȡȠ țȎ ȜȒțȜȚ Ȗ ȠȜȚ Ȕȓ ȫȠȎȔȓ, ȠȜȑȒȎ ȥȖȟșȜ ȖȟȣȜȒȜȐ ȜȝȖȟȎțțȜȑȜ ȜȝȩȠȎ, ȏșȎȑȜȝȞȖȭȠȟȠȐȡȬȧȖȣ țȎȟȠȡȝșȓțȖȬ ȟȜȏȩȠȖȭ A , ȞȎȐțȜ mA = 6 (ȐȟȓȑȜ ȓȟȠȪ ȦȓȟȠȪ ȫȠȎȔȓȗ).
ǽȜȫȠȜȚȡ, ȟȜȑșȎȟțȜ ȘșȎȟȟȖȥȓȟȘȜȚȡ ȜȝȞȓȒȓșȓțȖȬ ȐȓȞȜȭȠțȜȟȠȖ, P{A} = |
6 |
= |
1 |
» 0, 00013 . ȏ) ǾȎȟ- |
|||
6 |
6 |
6 |
5 |
||||
|
|
|
|||||
|
|
|
|
|
|||
ȟȚȜȠȞȖȚ ȠȜȠ Ȕȓ ȜȝȩȠ, ȥȠȜ Ȗ Ȑ ȝ. Ȏ). ǽȡȟȠȪ ȟȜȏȩȠȖȓ B ȟȜȟȠȜȖȠ Ȑ ȠȜȚ, ȥȠȜ Ȑȟȓ ȦȓȟȠȪ ȥȓșȜȐȓȘ ȐȩȗȒȡȠ țȎ ȞȎȕțȩȣ ȫȠȎȔȎȣ, ȠȜȑȒȎ ȥȖȟșȜ ȖȟȣȜȒȜȐ ȜȝȩȠȎ, ȏșȎȑȜȝȞȖȭȠȟȠȐȡȬȧȖȣ țȎȟȠȡȝșȓțȖȬ ȟȜȏȩȠȖȭ B ,
13

ȞȎȐțȜ mB = 6! (ȥȖȟșȜ ȝȓȞȓȟȠȎțȜȐȜȘ ȦȓȟȠȖ șȬȒȓȗ ȝȜ ȦȓȟȠȖ ȫȠȎȔȎȚ). ǽȜ ȘșȎȟȟȖȥȓȟȘȜȗ ȢȜȞȚȡșȓ
|
|
|
1 |
|
|
2 |
1 |
1 |
|
|
|
|
|
|||
ȐȓȞȜȭȠțȜȟȠȖ P{B} = |
6! |
= |
6 |
ɑ |
5 |
ɑ |
4 |
ɑ |
3 |
ɑ |
2 |
ɑ |
1 |
= |
5 |
. |
66 |
|
6 |
6 |
6 |
6 |
6 |
6 |
|
324 |
|
||||||
|
|
|
1 |
|
|
3 |
2 |
3 |
|
|
|
|
|
|||
45.ǽȓȠȭ Ȗ ǺȎȦȎ ȝȞȖȑșȎȦȓțȩ țȎ ȒȓțȪ ȞȜȔȒȓțȖȭ Ȑ ȘȜȚȝȎțȖȬ Ȗȕ ȒȓȟȭȠȖ ȥȓșȜȐȓȘ, ȐȘșȬȥȎȭ Ȗȣ, țȜ ȝȞȖȣȜȒȭȠ țȎ țȓȑȜ ȝȜȞȜȕțȪ, ȝȞȖȥȮȚ, ȘȎȘ Ȗ ȜȟȠȎșȪțȩȓ ȑȜȟȠȖ, Ȑ ȟșȡȥȎȗțȜȓ ȐȞȓȚȭ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ȜțȖ ȏȡȒȡȠ ȟȖȒȓȠȪ ȕȎ ȝȞȎȕȒțȖȥțȩȚ ȟȠȜșȜȚ ȞȭȒȜȚ, ȓȟșȖ ȣȜȕȭȖț ȞȎȟȟȎȔȖȐȎȓȠ ȑȜȟȠȓȗ ȟșȡȥȎȗțȩȚ ȜȏȞȎȕȜȚ, Ȏ ȟȠȜș, ȖȚȓȬȧȖȗ ȝȞȭȚȜȡȑȜșȪțȡȬ ȢȜȞȚȡ: Ȏ) ȟȠȜȖȠ Ȑ ȟȓȞȓȒȖțȓ ȘȜȚțȎȠȩ; ȏ) ȝȞȖȒȐȖțȡȠ Ș ȟȠȓțȓ.
46.ǰȜ ȐȞȓȚȭ ȑȞȜȕȩ țȎ ȡȥȎȟȠȘȓ ȚȓȔȒȡ 40-Ț Ȗ 70-Ț ȘȖșȜȚȓȠȞȎȚȖ ȠȓșȓȢȜțțȜȗ șȖțȖȖ ȝȞȜȖȕȜȦȮș ȜȏȞȩȐ ȝȞȜȐȜȒȎ. ǿȥȖȠȎȭ, ȥȠȜ ȜȏȞȩȐ ȜȒȖțȎȘȜȐȜ ȐȜȕȚȜȔȓț Ȑ șȬȏȜȗ ȠȜȥȘȓ, țȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ȜȏȞȩȐ ȞȎȟȝȜșȜȔȓț ȚȓȔȒȡ 40-Ț Ȗ 45-Ț ȘȖșȜȚȓȠȞȎȚȖ.
47.ǻȎ 200-ȘȖșȜȚȓȠȞȜȐȜȚ ȡȥȎȟȠȘȓ ȑȎȕȜȝȞȜȐȜȒȎ ȚȓȔȒȡ ȘȜȚȝȞȓȟȟȜȞțȩȚȖ ȟȠȎțȤȖȭȚȖ A Ȗ B ȝȞȜȖȟȣȜȒȖȠ ȡȠȓȥȘȎ ȑȎȕȎ, ȘȜȠȜȞȎȭ ȜȒȖțȎȘȜȐȜ ȐȜȕȚȜȔțȎ Ȑ șȬȏȜȗ ȠȜȥȘȓ ȑȎȕȜȝȞȜȐȜȒȎ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȖ ȟșȓȒȡȬȧȖȣ ȟȜȏȩȠȖȗ: Ȏ) ȡȠȓȥȘȎ ȞȎȟȝȜșȜȔȓțȎ țȓ ȒȎșȓȓ 20 ȘȚ ȜȠ A ȖșȖ B; ȏ) ȡȠȓȥȘȎ ȞȎȟȝȜșȜȔȓțȎ ȏșȖȔȓ Ș A, ȥȓȚ Ș B.
48.ǾȎȒȎȞ ȎȐȠȜȖțȟȝȓȘȠȜȞȎ ȖȚȓȓȠ ȠȜȥțȜȟȠȪ 10 ɤɦ Ȗ ȜȘȞȡȑșȭȓȠ ȟȐȜȖ ȝȜȘȎȕȎțȖȭ Ȑ
ɱ
ȏșȖȔȎȗȦȡȬ ȟȠȜȞȜțȡ. ǼȝȞȓȒȓșȖȠȪ, ȥȠȜ ȝȞȜȖȟȣȜȒȖȠ ȥȎȧȓ — ȞȎȒȎȞ ȜȘȞȡȑșȭȓȠ ȟȘȜ-
ȞȜȟȠȪ «Ȑ ȝȜșȪȕȡ ȐȜȒȖȠȓșȭ» ȖșȖ «Ȑ ȝȜșȪȕȡ DZǶǯDzDz»?
49.ǽȞȖ ȝȞȜȐȓȒȓțȖȖ ȖțȐȓțȠȎȞȖȕȎȤȖȖ Ȓșȭ ȜȝȞȓȒȓșȓțȖȭ ȖȚȓȬȧȓȑȜȟȭ țȎ ȟȘșȎȒȓ ȘȜșȖȥȓȟȠȐȎ ȔȖȒȘȜȑȜ ȣȖȚȖȥȓȟȘȜȑȜ ȞȓȎȘȠȖȐȎ ȖȟȝȜșȪȕȡȓȠȟȭ ȖȕȚȓȞȖȠȓșȪțȩȗ ȝȞȖȏȜȞ ȟ ȤȓțȜȗ ȒȓșȓțȖȭ ȦȘȎșȩ 0,2 ș. ǽȜȘȎȕȎțȖȭ ȝȞȖȏȜȞȎ ȜȘȞȡȑșȭȬȠȟȭ ȒȜ ȏșȖȔȎȗȦȓȑȜ ȒȓșȓțȖȭ ȦȘȎșȩ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ȜȦȖȏȘȎ ȜȘȞȡȑșȓțȖȭ țȓ ȝȞȓȐȩȟȖȠ 0,04 ș.
50.ǠȚȘȜȟȠȪ ȤȖȟȠȓȞțȩ Ȓșȭ ȣȞȎțȓțȖȭ ȏȓțȕȖțȎ țȎ ȎȐȠȜȕȎȝȞȎȐȜȥțȜȗ ȟȠȎțȤȖȖ ȞȎȐțȎ 50 Ƞ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȖ ȟȜȏȩȠȖȗ, ȟȜȟȠȜȭȧȖȣ Ȑ ȠȜȚ, ȥȠȜ ȝȞȖ ȟșȡȥȎȗțȜȗ ȝȞȜȐȓȞȘȓ Ȑ ȤȖȟȠȓȞțȓ ȏȡȒȓȠ ȜȏțȎȞȡȔȓțȜ: Ȏ) Țȓțȓȓ 5 Ƞ ȏȓțȕȖțȎ; ȏ) ȏȜșȓȓ 20 Ƞ ȏȓțȕȖțȎ; Ȑ) ȣȜȠȭ ȏȩ 1 Ƞ ȏȓțȕȖțȎ.
51.ǺȎȦȎ ȠȞȎȠȖȠ țȎ ȒȜȞȜȑȡ Ȑ ȖțȟȠȖȠȡȠ ȜȠ 40 ȒȜ 50 ȚȖț, ȝȞȖȥȮȚ șȬȏȜȓ ȐȞȓȚȭ Ȑ ȫȠȜȚ ȝȞȜȚȓȔȡȠȘȓ ȭȐșȭȓȠȟȭ ȞȎȐțȜȐȓȞȜȭȠțȩȚ. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ Ȑ ȒȓțȪ ȫȘȕȎȚȓțȎ ȜțȎ ȝȜȠȞȎȠȖȠ țȎ ȒȜȞȜȑȡ ȜȠ 45 ȒȜ 50 ȚȖț.
52.ȅȠȜȏȩ ȒȜȏȞȎȠȪȟȭ Ȑ ȖțȟȠȖȠȡȠ, ǽȓȠȭ ȚȜȔȓȠ ȐȜȟȝȜșȪȕȜȐȎȠȪȟȭ ȎȐȠȜȏȡȟȜȚ ȜȒțȜȑȜ Ȗȕ ȒȐȡȣ ȚȎȞȦȞȡȠȜȐ. ǮȐȠȜȏȡȟȩ ȝȓȞȐȜȑȜ ȚȎȞȦȞȡȠȎ ȟșȓȒȡȬȠ ȟ ȖțȠȓȞȐȎșȜȚ Ȑ 18 ȚȖț, ȐȠȜȞȜȑȜ ȚȎȞȦȞȡȠȎ — ȟ ȖțȠȓȞȐȎșȜȚ Ȑ 15 ȚȖț. ǻȎȗȠȖ ȐȓȞȜȭȠțȜȟȠȪ ȠȜȑȜ, ȥȠȜ ǽȓȠȭ ȏȡȒȓȠ ȔȒȎȠȪ ȎȐȠȜȏȡȟȎ țȓ ȏȜșȓȓ 10 ȚȖț.
ǾdzȆdzǻǶdz. ǰȩȏȓȞȓȚ Ȑ ȘȎȥȓȟȠȐȓ ȚțȜȔȓȟȠȐȎ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ W ȝȞȭȚȜȡȑȜșȪțȖȘ ȟȜ ȟȠȜȞȜțȎȚȖ T1 = 18 ȚȖț Ȗ T2 = 15 ȚȖț (ȞȖȟ. 1.3). ǿȜȏȩȠȖȓ A ȟȜȟȠȜȖȠ Ȑ ȠȜȚ, ȥȠȜ ȐȞȓȚȭ, ȘȜȠȜȞȜȓ ǽȓȠȭ
ȏȡȒȓȠ ȔȒȎȠȪ ȎȐȠȜȏȡȟȎ, ȚȓțȪȦȓ t = 10 ȚȖț. ȋșȓȚȓțȠȎȞțȩȓ ȟȜȏȩȠȖȭ, ȏșȎȑȜȝȞȖȭȠȟȠȐȡȬȧȖȓ țȎȟȠȡȝșȓțȖȬ ȟȜȏȩȠȖȭ A , ȕȎȦȠȞȖȣȜȐȎțȩ țȎ ȞȖȟ. 1.3. ǽȜȫȠȜȚȡ, ȟȜȑșȎȟțȜ ȑȓȜȚȓȠȞȖȥȓȟȘȜȚȡ ȜȝȞȓȒȓșȓțȖȬ
ȐȓȞȜȭȠțȜȟȠȖ, P{A} = |
V (A) |
|
T T |
2 |
- (T |
1 |
- t)(T |
2 |
- t) |
|
|
ɠ t |
ɰɠ t |
ɰ |
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
= 1- ɡ1 - |
ɱ |
- |
|
|
ɱ |
||||||
V (W) |
|
|
|
|
|
|
|
|
|
|
ɱɡ1 |
|
|
ɱ. |
||||||||||
|
|
|
|
|
T1T2 |
|
|
|
|
|
ɢɡ |
|
T1 ɲɢɱɡ |
|
T2 |
ɱɲ |
||||||||
ǽȞȖ T1 = 18 , T2 = 15 , t = 10 P{A} = 1 - |
(1 - |
10 |
)(1 - |
10 |
)= |
|
23 |
. |
|
|||||||||||||||
18 |
15 |
27 |
|
|||||||||||||||||||||
53. ǽȓȠȭ Ȗ ǺȎȦȎ ȒȜȑȜȐȜȞȖșȖȟȪ ȐȟȠȞȓȠȖȠȪȟȭ ȟ 12 ȒȜ 13 ȥ țȎ ȟȠȎțȤȖȖ ȚȓȠȞȜ «ǰȩȣȖțȜ» ȡ ȝȜȟșȓȒțȓȑȜ ȐȎȑȜțȎ ȝȜȓȕȒȎ, ȖȒȡȧȓȑȜ Ȑ ȤȓțȠȞ ȑȜȞȜȒȎ, ȜȒțȎȘȜ țȖ ȜȒȖț Ȗȕ țȖȣ țȓ
ǾȖȟ. 1.3. ǺțȜȔȓȟȠȐȜ ȫșȓȚȓțȠȎȞțȩȣ ȟȜȏȩȠȖȗ Ȑ ȕȎȒȎȥȓ 52
14
