Примеры заданий на контрольные работы

Часть 1. Механика, молекулярная физика и термодинамика

Контрольная работа № 1

Вариант 1

1. Пароход идет по реке от A до B со скоростью v₁ = 10 км/ч относительно берега, а обратно – со скоростью v₂ = 16 км/ч. Найти среднюю скорость парохода и скорость течения реки.

2. Прямой круглый однородный конус имеет массу m и радиус основания R. Найти момент инерции конуса относительно его оси.

3. Человек массой m = 60кг, бегущий со скоростью ν = 8 км/ч, вскакивает на тележку массой M = 80кг, движущуюся со скоростью u = 2,9 км/ч навстречу ему. С какой скоростью будет двигаться тележка?

4. Тело соскальзывает с плоскости, наклоненной под углом  = 8 к горизонту, и проходит по горизонтальной плоскости до остановки путь, равный пути, пройденному по наклонной плоскости. Определить коэффициент трения k, считая его постоянным в процессе всего движения тела.

Вариант 2

1. Камень брошен горизонтально со скоростью v_x = 15м/с. Найти нормальное а_n и тангенциальное а_ ускорения камня через время t = 1 c после начала движения.

2. Н а тонкостенный цилиндр намотана нить, конец которой закреплен (рис.). Нить остается параллельной наклонной плоскости с углом наклона  при разматывании. Какую скорость приобрел цилиндр, если его ось прошла расстояние l? Коэффициент трения между цилиндром и плоскостью k.

3. Тело массой m = 1кг, движущееся горизонтально со скоростью ν = 1 м/с, неупруго сталкивается с другим телом массой M = 0,5 кг. Какую скорость получат тела, если второе тело стояло неподвижно.

4. Мешок с песком сползает без начальной скорости с высоты H по гладкой доске, наклоненной под углом  = 60° к горизонту. После спуска мешок попадает на горизонтальный пол. Коэффициент трения мешка о пол k = 0,7. Где остановится мешок?

Контрольная работа № 2

Вариант 1

1. Математический маятник длиной l = 24,7 см совершает затухающие колебания. Через какое время t энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания  = 0,01.

2. Гиря массой m = 0,5 кг, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F=cos(t) Н. Определить для данной колебательной системы: 1) коэффициент затухания ; 2) резонансную амплитуду A_рез.

3. Найти разность фаз  колебаний двух точек, отстоящих от источника колебаний на расстояниях l₁ = 10 м и l₂ = 16 м. Период колебаний T = 0,04 с; скорость распространения c = 300 м/с.

4. В дне цилиндрического сосуда диаметром D = 0,5 м имеется круглое отверстие диаметром d = 1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты h этого уровня. Найти значение этой скорости для высоты h = 0,2 м.

Вариант 2

1. По грунтовой дороге прошел трактор, оставив следы в; виде ряда углублений, находящихся на расстоянии l = 30 см друг от друга. По этой дороге покатили детскую коляску, имеющую, две одинаковые рессоры, каждая из которых прогибается на x₀ = 2 см под действием груза массой m₀ = 1 кг. С какой скоростью v катили коляску, если от толчков на углублениях, она, попав в резонанс, начала сильно раскачиваться? Масса коляски M = 10 кг.

2. Собственная частота ₀ колебаний некоторой системы составляет 500 Гц. Определить частоту  затухающих колебаний этой системы, если резонансная частота _рез=499 Гц.

3. Два динамика расположены на расстоянии d=2,5 м друг от друга и воспроизводят один и тот же музыкальный тон на определенной частоте, который регистрируется приемником, находящимся на расстоянии l=3,5 м от центра динамиков. Если приемник передвинуть от центральной линии параллельно динамикам на расстояние x=1,55 м, то он фиксирует первый интерференционный минимум. Скорость звука v=340 м/с. Определить частоту звука.

4. В 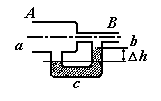оздух продувается через трубку АВ (см. рис.). За время t=1 мин. через трубку АВ протекает объем воздуха V = 5 л. Площадь поперечного сечения широкой части трубки АВ равна S₁ = 2 см², а узкой ее части – S₂ = 0,5 см². Найти разность уровней h воды, налитой в трубку acb. Плотность воздуха  = 1,32 кг/м³.

Контрольная работа № 3

Вариант 1

1. Сосуд разделен перегородками на три части, объемы которых равны V₁, V₂ и V₃ и в которых находятся газы при давлениях p₁, p₂ и p₃ соответственно. Какое давление в сосуде установится после удаления перегородок, если температура при этом осталась неизменной?

2. Массовые доли водорода, азота и неона газовой смеси равны соответственно 0.1, 0.7 и 0.2. Определить молярную массу смеси и ее удельную теплоемкость при постоянном объеме.

3. Идеальный газ совершает круговой процесс, состоящий из двух изотерм и двух изохор. Изотермические процессы протекают при температурах T₁ и T₂ (T₁ > T₂), изохорические – при объемах V₁ и V₂. (V₂ в «e» раз больше V₁). Найти к.п.д. η цикла. Известен показатель адиабаты .

4. Гелий массы m = 1,7 г адиабатически расширили в n = 3,0 раза и затем изобарически сжали до первоначального объема. Найти приращение энтропии газа в этом процессе.

Вариант 2

1. Воздушный шар объемом 240 м³, заполненный водородом при температуре 300 К, поднимает полезный груз массой 300 кг. Какой полезный груз сможет поднять воздушный шар, если его заполнить горячим воздухом при температуре 400 К? До какой температуры нужно нагреть воздух, чтобы воздушный шар смог поднять такой же полезный груз, как и при заполнении его водородом? Молярная масса воздуха μ = 0,029 кг/моль.

2. Найти удельную теплоемкость c_p газовой смеси, состоящей из 3000 молей аргона и 2000 молей азота.

3. Для нагревания некоторой массы газа на t₁ = 50°C при p = const необходимо затратить количество теплоты Q₁ = 670 Дж. Если эту массу газа охладить на Δt₂ = 100°C при V = const, то выделяется теплота Q₂ = 1005 Дж. Какое число степеней свободы, i имеют молекулы этого газа?

4. Найти приращение энтропии двух молей идеального газа с показателем адиабаты  = 1,30, если в результате некоторого процесса объем газа увеличился в  = 2,0 раза, а давление уменьшилось в  = 3,0 раза.