Контрольні питання

1. Що розуміють під математичною постановкою гідромеханічної задачі?

2. Чому рівняння нерозривності фільтраційного потоку являє собою рівняння балансу маси флюїду?

3. Запишіть закон Дарсі у векторному вигляді.

4. Як змінюються в’язкість і густина нафти залежно від тиску?

5. Запишіть і поясніть рівняння стану рідини.

6. Запишіть і поясніть рівняння стану реального газу.

7. Запишіть і поясніть залежності коефіцієнтів пористості та проникності пористого середовища від тиску флюїдів.

8. Що розуміють під функцією Лейбензона?

4 Усталена фільтрація нестисливої рідини в пористому пласті до галереї і свердловини за законом дарсі

4.1 Виведення диференціального рівняння усталеної фільтрації нестисливої рідини в пористому пласті за законом Дарсі

Для нестисливої рідини, наприклад для нафти, густина _=const. Тоді згідно із рівнянням (3.5) функція Лейбензона

, (4.1)

а отже шукане диференціальне рівняння отримуємо з узагальненого рівняння (3.6) у вигляді рівняння Лапласа щодо тиску р:

, (4.2)

або

. (4.3)

4.2 Усталена прямолінійно-паралельна фільтрація нестисливої рідини в пористому пласті за законом Дарсі

Тут маємо випадок одновимірної фільтрації до галереї (рис. 4.1). Диференціальне рівняння Лапласа (4.3) відповідно набуває вигляду:

або . (4.4)

оскільки тиск р залежить тільки від одної координати х.

Граничні умови:

, (4.5)

де p_к, p_г – тиск відповідно на контурі пласта і на стінці галереї; L – довжина пласта.

Задача повністю поставлена. Інтегруючи двічі рівняння (4.4), отримуємо загальний розв’язок рівняння, тобто:

_(4.6)

Довільні постійні інтегрування с₁ і с₂ знаходимо з граничних умов (4.5)

(4.7)

у вигляді:

Підставляючи с₁ і с₂ у рівняння (4.6), дістаємо рівняння розподілу тиску вздовж пласта (рівняння п’єзометричної лінії)

. (4.8)

Диференціюючи рівняння (4.8), маємо вираз градієнта тиску

(4.9)

Із загальної формули закону Дарсі

, (4.10)

оскільки dl = dx, маємо формулу закону Дарсі стосовно до прямолінійно-паралельного потоку:

, (4.11)

де dl – довжина шляху фільтрації.

Підставляючи вираз (4.9) у формулу (4.11), записуємо формулу швидкості фільтрації:

, (4.12)

а помноживши швидкість v на площу фільтрації F – формулу дебіту галереї:

. (4.13)

Із рівняння (4.8) випливає, що тиск р у довільній точці пласта є лінійною функцією координати x, а п’єзометрична лінія представлена прямою лінією (див. рис. 4.1). Із рівняння (4.8) також випливає, що тиск однаковий в усіх точках пласта, для яких

. (4.14)

Рівняння (4.14) є рівнянням ізобар (ліній рівного тиску). Сукупність ліній течій та ізобар називають гідродинамічним полем потоку (гідродинамічною сіткою) на горизонтальній площині (рис. 4.2). Поверхнями рівного тиску в такому потоці є вертикальні площини, перпендикулярні лініям течії. Гідродинамічне поле представлено еквівалентними (рівновіддаленими) прямими лініями (див. рис. 4.1), причому лінії течії перпендикулярні до ізобар (властивість гідродинамічного поля). Лінії ізобар на горизонтальній площині утворюють карту ізобар. Лінії ізобар є рівновіддаленими одна від одної прямими, перпендикулярними до осі Ох, а лінії течії (траєкторії частинок рідини) є рівновіддаленими прямими, паралельними осі Ох (рівновіддаленість одна від одної ліній течій означає однакову витрату рідини між ними). Під час побудови карти ізобар значини ізобар змінюють в арифметичній прогресії, а їх координати х також відповідно змінюються в арифметичній прогресії.

Рис. 4.2 – Гідродинамічне поле усталеного прямолінійно-паралельного фільтраційного потоку

Із рівнянь (4.9), (4.12) і (4.13) видно, що , v і Q є постійними величинами, що не залежать від просторової координати x (рис. 4.3).

Рис. 4.3 – Зміна характеристик усталеного прямолінійно-паралельного фільтраційного потоку вздовж лінії течії (вздовж осі Ох)

Визначимо середній тиск у пласті (середньозважений за об’ємом)

, (4.15)

де – середній тиск у пласті; V_п – об’єм пор пласта; p – тиск у довільній точці пласта.

Оскільки об’єм пор V_п = LFm, dV_п = Fmdx, то з урахуванням рівняння (4.8) знаходимо:

(4.16)

тобто середній тиск у пласті

Тут результат взагалі очевидний, бо залежність p(x) є прямою лінією.

Для визначення часу руху частинок рідини використаємо вже відомий зв’язок (1.5) між дійсною швидкістю w та швидкістю фільтрації v і запишемо:

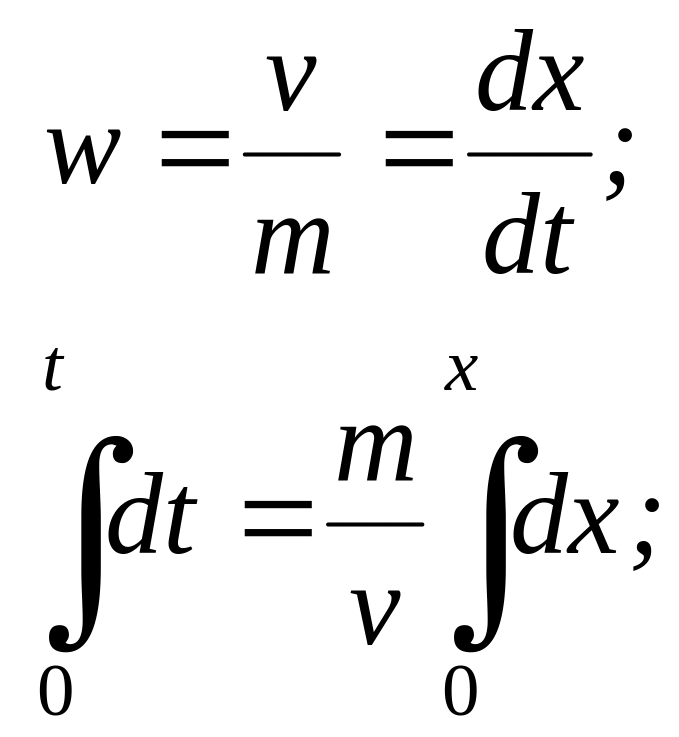(4.17)

(4.18)

або

. (4.19)

Повний час руху частинок рідини від контура живлення пласта до галереї (x = L)

, (4.20)

де V_зап = LFm – об’єм запасу нафти в пласті.