10.3 Розв’язування задачі фільтрації газу з допомогою рівняння матеріального балансу

Під час відбирання газу із газового покладу можуть проявлятися газопружний (газовий) або газоводопружний (пружногазоводонапірний) режими. На газовому режимі роботи пласта приплив газу до свердловин відбувається за рахунок сил пружності газу, а на пружногазоводонапірному – у тому числі також і сил пружності води навколишньої водоносної області. Перший з них має місце в закритому газовому покладі, другий – у відкритому.

В основу теорії проектування розробки газових покладів покладено рівняння матеріального балансу. Суть його полягає в тому, що кількість газу, видобутого з покладу за деякий проміжок часу, дорівнює зменшенню кількості газу в пласті. Таке рівняння справедливе тільки стосовно газового режиму, а за умов пружногазоводонапірного режиму ще треба врахувати пружний запас водоносної області.

Масовий запас газу в закритому покладі

, (10.40)

а його зміна

, (10.41)

де V_п – об’єм пор пласта (стосовно до газового режиму ); - густина газу, що відповідає середньозваженому тиску у пласті; знак “–“ вказує, що прирости і протилежні за знаком.

Відібрана (нагромаджена) маса газу за такий же проміжок часу

, (10.42)

звідки

. (10.43)

де Q_м(t) – масовий дебіт газу, змінний в часі t.

Прирівнюючи зміни мас газу, дістаємо диференціальне рівняння виснаження газового покладу

(10.44)

або

. (10.45)

Відомо, що у випадку фільтрації газу до свердловини середній тиск , де p_к – тиск на контурі пласта. Тоді записуємо:

. (10.46)

Розглянемо розв’язки рівняння (10.46) за умов окремо і .

У разі , інтегруючи рівняння (10.46), одержуємо зміну тиску p_к на контурі пласта в часі:

, (10.47)

де p_п – початковий тиск на контурі пласта.

Оскільки дебіт газової свердловини (див. підрозд. 8.3)

, (10.48)

то звідси знаходимо вибійний тиск

(10.49)

а з урахуванням (10.47) отримуємо величину вибійного тиску як функцію часу в випадку виснаження газового покладу за умови у вигляді:

. (10.50)

У разі підставляємо формулу дебіту (10.48) у диференціальне рівняння (10.46), розділяємо змінні та інтегруємо, тоді одержуємо зв’язок між контурним тиском p_к(t) і часом t, тобто

; (10.51)

; (10.52)

. (10.53)

Задаючись значинами контурного тиску p_к , причому , знаходимо ряд значин часу t за формулою (10.53) і ряд значин дебіту Q₀ за формулою (10.48), а отже зміну контурного тиску p_к і дебіту свердловини Q₀ у часі t.

Рівняння (10.53) можна перетворити ще й так:

;

;

, (10.54)

де ; .

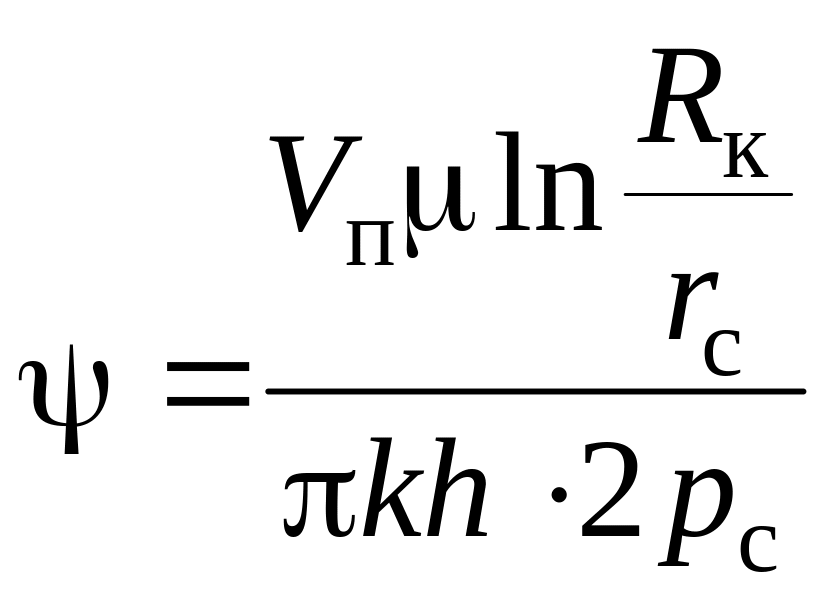Дебіт свердловини на основі формули (10.48) записуємо у вигляді:

(10.55)

а ввівши безрозмірний дебіт з урахуванням формули (10.54), знаходимо:

або

(10.56)

Із формули (10.54) видно, якщо , , то , а із формули (10.48) маємо, що в такому разі .

Якщо вибійний тиск , то рівняння (10.52) набуває вигляду:

,

звідки маємо

;

(10.57)

або

(10.58)

Графіки зміни в часі параметрів роботи покладу за різних умов показано на рис. 10.1.

Контрольні питання

1. Виведіть рівняння Лейбензона. Як його розв’язують?

2. Запишіть і поясніть аналогію між неусталеною фільтрацією пружної рідини та газу. Покажіть приклад застосування аналогії.

3. Виведіть диференціальне рівняння виснаження газового покладу.

4. Покажіть розв’язок диференціального рівняння виснаження газового покладу за умови заданого постійного дебіту. Поясніть зміну параметрів роботи покладу в часі.