1.3 Границі застосування закону Дарсі. Нелінійні закони фільтрації

Експериментально встановлено, що закон Дарсі порушується внаслідок дії:

1) інерційних сил за великих швидкостей фільтрації, тобто за великих градієнтів тиску (верхня межа справедливості закону Дарсі);

2) так званих нелінійних ефектів за малих градієнтів тиску, що пов’язані з неньютонівськими властивостями рідини та молекулярноповерхневою взаємодією насичуючого флюїду з твердим скелетом пористого середовища (нижня межа справедливості закону Дарсі).

Ці причини ведуть до нелінійних законів фільтрації. Нелінійність законів фільтрації ще пов’язується також з деформацією гірських порід за великих перепадів тиску і, як результат, із нелінійною зміною коефіцієнта проникності порід від тиску.

Першу кількісну оцінку верхньої межі дав М.М.Павловський залежно від критерію (числа) Рейнольдса Re (критерій Рейнольдса визначає співвідношення між силами інерції та силами в’язкого тертя в рухомій рідині чи газі), тобто за Re < Re_кр справедливим є лінійний закон Дарсі, а за Re > Re_кр – нелінійний закон, де Re_кр – критична значина числа Рейнольдса, коли порушується закон Дарсі.

Пізніше за аналогією із загальною трубною гідравлікою, виходячи з формули Дарсі-Вейсбаха

, (1.23)

шукали залежність між коефіцієнтом гідравлічного опору (числом Ейлера)

(1.24)

і критерієм Рейнольдса

, (1.25)

де λ – коефіцієнт гідравлічного опору; d – характерний лінійний розмір пористого середовища, що характеризує його з геометричної точки зору (діаметр труби); U – характерна швидкість руху рідини; υ – кінематичний коефіцієнт в’язкості рідини. Такий підхід грунтується на тому, що з порівняння формули Пуазейля, яка випливає з формули Дарсі-Вейсбаха за ламінарного режиму, і формули закону Дарсі маємо аналогію між коефіцієнтом проникності k та величиною , тобто пористе середовище з геометричної точки зору треба характеризувати лінійним розміром. Різні автори за U та d брали різні величини ( і т. д.), тому одержали безліч різних формул. Ці формули не мають принципових переваг одна перед другою і однаково зручні для практичного використання. Приклад залежності λ від Re показано на рис. 1.2.

Рис. 1.2 – Експериментальна залежність λ(Re), коли , (за Ф.І. Котяховим і Г.Ф. Требіним); цифрами на рисунку позначено різні зразки пористих середовищ

У практиці розробки газонафтових родовищ найчастіше використовується формула В. М. Щелкачова:

, (1.26)

критична значина для якої Re_ккрр = 0,032...14. Широкий діапазон зміни пояснюється тим, що в неповній мірі формула враховує особливості структури пористого середовища. Крім того, має вплив плавний перехід від лінійного закону (режиму) фільтрації до нелінійного. Коефіцієнт λ відповідно до цієї формули

(1.27)

Зазначимо, що за ламінарність потоку не порушується; турбулентність проявляється за значно більших значин Re, ніж Re_кр.

Швидкість фільтрації, за якої порушується закон Дарсі у верхній границі, називають критичною швидкістю фільтрації v_кр. Її можна визначити з формули (1.26) за Re = Re_кр (з розрахунковим запасом рекомендується брати Re_кр = 1) або графічно, виходячи з експериментальних даних (рис. 1.3).

Рис.1.3 – Залежність швидкості фільтрації від градієнта тиску за експериментальними даними

За лінійний закон Дарсі перестає бути справедливим, наступає область справедливості нелінійного закону. Останній прийнято виражати такими формулами:

1) степеневою (одночленною або Смрекера)

; (1.28)

2) двочленною (Проні або Форхгеймера)

, (1.29)

де k_к – коефіцієнт пропорціональності (можна назвати коефіцієнтом Красно­польського); n – показник режиму фільтрації ( ), причому n є функ­цією швидкості v і тільки за малої зміни v можна брати ; a, b – постійні експериментальні коефіцієнти, причому коефіцієнт a характеризує сили в’язкого тертя, а коефіцієнт b – інерційні сили.

За n = 1 з формули (1.28) маємо закон Дарсі, а за n = 0,5 – квадратичний закон Краснопольського.

Із формули (1.29) у разі великих швидкостей, коли нехтуємо першим членом і дістаємо квадратичний закон; за малих швидкостей, коли нехтуємо другим членом, що характеризує інерційні сили, дістаємо безінерційний закон Дарсі, причому

. (1.30)

Коефіцієнт b можна оцінити, наприклад, за формулою А. Й. Ширковського:

. (1.31)

У газопромисловій справі ще записують: ; (див. гл. 2), або , де k_ρ, , с – експериментальні константи пористого середовища; l – коефіцієнт макрошорсткості, який характеризує внутрішню структуру порового простору, причому k_ρ=l=1/ с= . Величини k_ρ, , с, l можна оцінити з формули (1.31).

За статистичними даними багатьох досліджень встановлено емпіричну залежність

, (1.32)

де l вимірюється в метрах, а k – в м².

Тоді двочленну формулу нелінійного закону, наприклад, можна записати

. (1.33)

Відзначимо, що коефіцієнт проникності k характеризує усереднений масштаб пористого середовища (ефективний діаметр зерен, питому поверхню і т.п.), а коефіцієнт k_ρ (аналогічно с’, l’) – усереднені показники геометричної структури (кількість звужень пор, ступінь стиснення струменів рідини та інші). Причому перший характеризує пористе середовище для ідеальної в’язкої рідини, а другий – для ідеальної вагової рідини. Між ними немає певного аналітичного зв’язку, хоч статистично на основі експериментів зв’язок встановлено.

Двочленна формула є фізично найбільш обгрунтованою, оскільки враховує одночасну дію в’язких та інерційних сил, що проявляються різною мірою за різних швидкостей фільтрації (чи за різних градієнтів тиску). З двочленної формули, записаної у вигляді

, (1.34)

зіставляючи ці сили з силою тиску (з градієнтом тиску), можна двояко одержати:

(1.35)

або

. (1.36)

Позначивши маємо:

(1.37)

або

. (1.38)

Тут Eu - число Ейлера, яке характеризує співвідношення сил тиску та інерції; Da - число Дарсі, яке характеризує співвідношення в’язкісних сил і сил тиску; Re^* - критерій Рейнольдса, де характерні лінійний розмір і швидкість представлено величинами відповідно kс і v.

Із рівнянь (1.37) і (1.38) маємо, що закон Дарсі справедливий за чи , або іншими словами за . Залежність (1.37), яку запропонував М.П. Лебединець (використав результати багатьох експериментів різних дослідників за m = 0,18-0,36, k = 0,46-2200 мкм², с = 9,3·10³ – 1,5·10⁷ м^-1), графічно показано на рис. 1.4. Звідси з похибкою не більше 1% можна прийняти, що за справедливим є закон Дарсі ( ), за – квадратичний закон, а в інтервалі 0,01< Re*< 100 – двочленна формула нелінійного закону (перехідна область або мішана фільтрація).

Рис. 1.4 – Експериментальна залежність Eu(Re*)

Порушення закону Дарсі за малих градієнтів тиску(в нижній границі) буде розглянуто дальше в окремому розділі.

Контрольні питання

1. Чому закон Дарсі називають лінійним законом фільтрації?

2. Як встановити границі справедливості закону Дарсі?

3. Чому двочленна формула нелінійного закону фільтрації вважається фізично найбільш обгрунтованою?

4. Поясніть фізичний зміст критеріїв Рейнольдса, Ейлера та Дарсі.

2 ПРИНЦИПИ СХЕМАТИЗАЦІЇ ПРИРОДНИХ УМОВ

І МОДЕЛЮВАННЯ ПРОЦЕСІВ ФІЛЬТРАЦІЇ

Практична цінність результатів гідродинамічного дослідження процесів фільтрації залежить від правильності вибору розрахункової схеми пласта і створення моделі процесу фільтрації.

2.1 Принципи схематизації природних умов

для гідрогазодинамічних розрахунків

Для гідрогазодинамічних розрахунків природні умови нафтогазоводо­носних пластів необхідно надійно і досить повно вивчити, відповідним чином диференціювати, серед них виділити головні, визначальні чинники, а сама природна обстановка має бути подана у вигляді розрахункової схеми. Для побудови розрахункової схеми кожний продуктивний пласт слід розглядати як єдину гідродинамічно пов’язану систему не тільки в усій області нафтогазо­носності, але й включаючи і навколишню водонапірну область. У середині цієї системи розподіли тисків, швидкостей і витрат рідини (газу) визначаються початковими та граничними умовами. У результаті дістаємо область пласта, що обмежена поверхнями, на яких задано граничні умови, а в усій області пласта – початкові умови.Тобто задачі підземної гідрогазомеханіки є задачами математичної фізики.

На поведінку газонафтового покладу під час відбирання флюїдів (нафти, газу та води) впливають геометричний характер покладу (форма, розміри, взаємне розміщення нагромаджень кожного із флюїдів), режим роботи пласта і штучно створені нами умови розробки, структурно-тектонічні та фаціально-літологічні властивості пласта, властивості порід і флюїдів, пластові тиск і температура. Розглянемо коротко ці умови.

1. Нафта (газ) залягає в пласті переважно антиклінальної форми, що обмежений зверху (покрівля) і знизу (підошва) непроникними породами (рис. 2.1, а), тобто залягає в пастці.

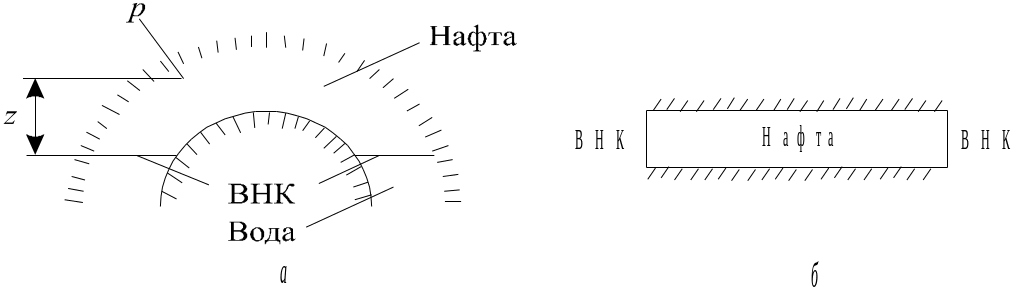
Рис.2.1 – Реальний (а) і схематизований (б) пласти

У кожній точці пласта за відсутності фільтрації (відбирання флюїдів) гідростатичний тиск різний, тому під тиском завжди розуміємо зведений тиск

, (2.1)

де p – гідростатичний тиск у заданій точці;  – густина рідини; g – прискорення вільного падіння; z – висота положення заданої точки над площиною порівняння, за яку звичайно беруть водонафтовий (ВНК) чи водогазовий (ВГК) контакт. Таким чином, пласт начебто вирівнюється і стає горизонтальним; далі розглядатимемо такі пласти (рис. 2.1, б).

Рис.2.2 – Схематизація потоків у пласті: 1-пласт; 2-п’єзометрична лінія

2. За різною величиною напору (тиску) розрізняють такі потоки (рис. 2.2):

а) напірні (п’єзометрична лінія розміщена вище непроникної покрівлі пласта);

б) безнапірні, або самоплинні (п’єзометрична лінія збігається з вільною поверхнею потоку, тобто розміщена нижче верхньої межі пласта);

в) напірно-безнапірні (поєднання перших двох; характеризуються різним положенням п’єзометричної лінії на різних ділянках пласта; розв’язки одержуються з розв’язків для перших двох потоків так званим методом "зшивання" на межі їх поділу).

3. За співвідношенням тиску в пласті p і тиску насичення нафти газом p_нас виділяють однорідну нестисливу (густина ρ ═ const) або пружну (ρ ≠ const) нафту ( ) і газовану (суміш нафти і вільного газу) нафту ( ).

4. Залежно від термогідродинамічних умов пласта і штучно створених умов видобування нафти можуть проявлятися різні режими роботи пласта. Режимом роботи пласта називають проявлення переважаючого виду пластової енергії або сил, що зумовлюють приплив рідин і газів до свердловин. Умовно в "чистому" вигляді за переважаючим видом енергії виділяють шість режимів:

а) водонапірний (жорсткий водонапірний), за яким нафта й газ витісняються під напором природних або штучно закачуваних вод, коли p > p_нас;

б) газонапірний (іноді називають режим газової шапки), коли нафта разом з вільним газом витісняється до свердловин під напором стиснутого газу, що знаходиться над нафтою у вигляді газової шапки за ;

в) режим розчиненого газу (режим газованої нафти), коли p < p_нас і пухирці газу, що виділяються з нафти внаслідок зниження тиску, розши­рюючись, витісняють нафту до свердловин (зрозуміло, що в пласті рухається газована нафта);

г) пружний, за якого флюїди рухаються до свердловин завдяки пружному розширенню самих флюїдів і скелета породи пласта в результаті зниження тиску (у нафтовому покладі за p > p_нас);

ґ) гравітаційний, коли основною і єдиною силою є сила ваги самої нафти (чи води у водяному пласті), яка має вільну поверхню;

д) мішаний, за якого можливе одночасне проявлення енергій розчиненого газу, пружності та напору води (його часто розглядають як витіснення газованої нафти водою за p < p_нас).

Стосовно газових і газоконденсатних родовищ виділяють два режими:

а) газовий (точніше газопружний), коли рух газу відбувається за рахунок потенціальної енергії розширення газу внаслідок зниження тиску;

б) пружноводонапірний, за якого рух газу відбувається за рахунок енергії розширення газу та напору пластової води.

5. У ході створення розрахункової схеми пласта необхідно враховувати взаємне розміщення свердловин відносно границь області фільтрації чи границь поділу між зонами з різною проникністю. Ці границі мають неправильні обриси та геометричну форму. Тому їх схематизують у прямолінійні та кругові форми, виділяючи: а) безмежний пласт (у разі значного віддалення свердловин від границь області фільтрації); б) напівобмежений (з однією прямолінійною границею); в) нескінчену смугу з двома паралельними прямолінійними нескінченними границями; г) прямокутник (смугоподібний пласт); ґ) круг; д) кільце. Прямокутник і круг використовуються як основні форми.

6. Відповідно до схематизації меж області фільтрації в прямолінійні та кругові виділяють три типи фільтраційних потоків: а) прямолінійно-паралельний; б) плоскорадіальний; в) радіально-сферичний (рис. 2.3).

Для прямолінійно-паралельного потоку характерна прямолінійність і паралельність траєкторій руху всіх частинок рідини, причому у будь-якому перпендикулярному до напряму руху перерізі потоку швидкості фільтрації не тільки паралельні, але й рівні між собою (див. рис. 2.3, а). Зрозуміло, що тиск у кожній точці під час стаціонарного руху буде функцією тільки однієї координати x. Такий потік ще називають одновимірним, плоско-паралельним, паралельно-струминним. Його спостерігають у лабораторних умовах під час руху рідини (газу) вздовж циліндричного керна, а також у пласті на деякій відстані від свердловин, що розміщені вздовж прямої лінії у вигляді ряду. Якщо ущільнити свердловини на цій лінії, замінити суцільною прямолінійною щілиною, то такий ряд називають галереєю. Таку галерею умовно можна виділити на певній відстані від свердловин, коли рух буде прямолінійно-паралельним (див. рис. 2.3, б).

Рис. 2.3 – Типи фільтраційних потоків стосовно різних меж області фільтрації: 1 – траєкторія руху частинок рідини; 2 – нагнітальна свердловина; 3 – видобувна свердловина

Плоско-радіальний потік має місце під час руху рідини в горизонтальному пласті до гідродинамічно досконалої свердловини, тобто до такої свердловини, яку пробурено на всю товщину пласта і не обсаджено колоною обсадних труб. Частинки рідини рухаються паралельно одній і тій же площині, наприклад підошві пласта, тобто потік плоским (див. рис. 2.3, в). Для його характеристики в кожній точці (т. М) необхідно знати дві координати – x та y, тому він є двовимірним (див. рис. 2.3, г). Але частинки рухаються вздовж прямих, що радіально сходяться в одній точці (центрі свердловини), тобто потік є радіальним або плоско-радіальним. Його можна описати одним радіусом-вектором , тобто цей потік характеризується осьовою симетрією. Звідси назви: одновимірний з осьовою симетрією, або одновимірний осесиметричний потік.

Якщо траєкторії частинок не паралельні якійсь площині, то такий потік називають просторовим, або тривимірним, оскільки для його характеристики необхідно знати три координати x, y, z. Якщо траєкторії прямолінійні й радіально сходяться в одній точці (центрі), то такий потік називають сферично-радіальним. Для нього радіус-вектор , а сам потік характе­ризується центральною симетрією, тобто він є потоком одновимірним з центральною симетрією. Такий потік може бути в напівобмеженому пласті, коли свердловина з’єднана з ним напівсферичним вибоєм (див. рис. 2.3, д). Ця схема є допоміжною і використовується для розв’язування деяких задач.