Контрольні питання

1. Запишіть і поясніть аналогію між фільтраціями нестисливої рідини та стисливого флюїду.

2. Чому лійка депресії тиску крутіша в разі фільтрації газу, ніж у разі фільтрації нестисливої рідини? Поясніть формулами та графічно.

3. Чому дорівнює середній тиск у коловому газовому пласті під час фільтрації до свердловини?

4. Нарисуйте можливі індикаторні діаграми в разі фільтрації в газовому пласті. Запишіть їхні рівняння.

5. Як враховують реальні властивості газу для обчислення дебіту газової свердловини? Запишіть необхідні формули.

9 Неусталена фільтрація пружної рідини в пористому пласті

9.1 Виведення диференціального рівняння неусталеної фільтрації пружної рідини

Нами вище одержано узагальнене диференціальне рівняння ізотермічної фільтрації пружного флюїду за законом Дарсі в деформівному пористому пласті за умов і у вигляді:

. (9.1)

Для виведення шуканого диференціального рівняння використовуємо рівняння стану пружної рідини й пористого середовища:

; (9.2)

. (9.3)

Спочатку знаходимо добуток , помноживши рівняння (9.2) на рівняння (9.3), тобто

(9.4)

Позначаємо:

, (9.5)

де * – коефіцієнт пружної ємності насиченого пласта.

Оскільки _р і _с мають порядок 10^-10 Па^-1, а різниця – 10⁷ Па, то третім доданком у рівнянні (9.4) через малу його значину можна нехтувати порівняно з першими двома. Тоді

. (9.6)

Далі обчислюємо функцію Лейбензона для пружної рідини:

. (9.7)

Оскільки , то наближено приймаємо функцію Лейбензона для пружної рідини таку:

. (9.8)

Продиференціювавши рівняння (9.6) і (9.8) та підставивши результат у рівняння (9.1), одержуємо шукане диференціальне рівняння неусталеної фільтрації пружної рідини в недеформівному пористому пласті за законом Дарсі, коли коефіцієнт нафтонасиченості , у вигляді:

, (9.9)

або

, (9.10)

де – коефіцієнт п’єзопровідності пласта, .

Рівняння (9.10) називають основним диференціальним рівнянням пружного режиму фільтрації або рівнянням п’єзопровідності. Воно відоме в математичній фізиці як рівняння Фур’є або рівняння теплопровідності. Звідси за аналогією з коефіцієнтом температуропровідності В.М. Щелкачов коефіцієнт назвав коефіцієнтом п’єзопровідності. Коефіцієнт п’єзопровідності нафтогазовмісних порід змінюється в основному від 0,1 до 5 м²/с.

9.2 Особливості фільтрації рідини в пласті за наявності пружного режиму

Умова пружного режиму – перевищення тиску р в будь-якій точці пласта, в тому числі на вибоях свердловин, над тиском насичення нафти газом р_нас, тобто . При цьому нафта знаходиться в однофазному стані (без вільного газу).

Приплив нафти до свердловин відбувається за рахунок енергії пружності рідини (нафти), зв’язаної (залишкової) води і гірської породи – енергії їх пружного розширення. Під час зниження тиску в пласті збільшуються об’єми нафти та зв’язаної води і зменшується об’єм пор; об’єм нафти, відповідний цим змінам, надходить у свердловини.

Пружності рідин і породи пласта незначні. Тому залежно від конкретних умов їх розглядають і як нестисливі, і як стисливі, пружні, хоча взагалі кажучи, нестисливих рідин не існує. Згідно із законом Гука для насиченого рідиною пласта можна записати відносну зміну об’єму рідини:

, (9.11)

де V – початковий об’єм рідини; V – зміна об’єму рідини за зміни тиску р; * – коефіцієнт пружної ємності (об’ємної пружності) насиченого пласта.

Оскільки для нафти _н = (7-20)·10^-10 Па^-1, для води _в = (2,7-5)·10^-10 Па^-1, для гірської породи _п = (0,3-2)·10^-10 Па^-1, то за т₀ = 0,2 маємо:

а) для нафтонасиченого пласта

 Па^-1  Па^-1, Па^-1= Па^-1;

б) для водонасиченого пласта

т₀_в=0,2310^-10 Па^-1 = 0,610^-10 Па^-1, Па^-1= Па^-1;

в) для нафтонасиченого пласта з урахуванням залишкової (чи пластової) води

де індекси н, в, п означають відповідно нафту, воду й породу, ; – коефіцієнт насиченості пор зв’язаною водою; – коефіцієнт насиченості пор нафтою.

Звідси слідує, що доданки в рівнянні (9.5) близькі за величиною і нехтувати пружністю пласта чи рідини (нафти або води) не можна. Якщо взяти , то Па^-1 Па = 0,01 або 1%, тобто зміна об’єму рідини (нафти) невелика. Але якщо врахувати величезні об’єми нафти і, особливо, води в покладі, то завдяки пружності можна відібрати із пласта великі об’єми нафти.

Об’єм рідини, який можна одержати з пласта за рахунок пружності, називають пружним запасом пласта:

. (9.12)

Пружність пласта особливо відчутно проявляється після пуску свердловини в роботу або після її зупинки. Створене у свердловині збурення тиску (депресія тиску) поширюється вглиб пласта, навколо свердловини утворюється депресійна лійка, яка збільшується (розширюється) з часом (рис. 9.1). Відтак депресійні лійки окремих свердловин, поширюючись, зливаються, утворюється загальна депресійна лійка, яка в міру відбирання нафти поширюється до меж пласта. На цьому закінчується перша фаза пружного режиму.

Якщо поклад літологічно чи тектонічно обмежений (замкнутий), то надалі наступає друга фаза пружного режиму, коли появляється різновид пружного режиму – замкнуто-пружний режим. При цьому на контурі обмеження пласта, що збігається з контуром нафтоносності, тиск зменшується з часом; зменшується також тиск у покладі.

Якщо поклад не обмежений (відкритий), то загальна депресійна лійка поширюватиметься в позаконтурну водоносну область, яка може бути значною за розмірами й гідродинамічно зв’язаною з покладом. Пружний режим переходить у другий різновид – пружноводонапірний режим. Він зумовлений як пружністю, так і напором крайових вод у водоносній області.

Для замкнуто-пружного та пружноводонапірного режимів характерно значне зниження тиску в початковий період за постійного поточного відбору (дебіту) нафти (або зниження поточного відбору за постійної депресії тиску). На пружноводонапірному режимі темп подальшого зниження тиску (поточного відбору) сповільнюється, оскільки зона збурення охоплює щораз більші об’єми водоносної області і для одного і того ж відбору нафти необхідно вже створити менше зниження тиску. Якщо зовнішня межа водоносної області знаходиться на вищій гіпсометричній висоті, то тиск на межі може стабілізуватися на певній величині, а режим переходить в усталений водонапірний режим, коли тиск на контурі живлення пласта .

Таким чином, пуск свердловини (чи зміна відбору) викликає тривалі процеси перерозподілу тиску в пласті.

З часом неусталені процеси, викликані збуренням, стабілізуються. Далі показано, що радіус межі зони збурення на певний момент часу, наприклад,

, (9.13)

звідки можна записати оцінку часу стабілізації тиску в пласті

, (9.14)

де R – радіус контура пласта або, точніше, радіус зони збурення тиску.

Розглянуте ілюструють рис. 9.2-9.6. На рис. 9.2 показано характер розподілу тиску в нескінченному пласті після пуску свердловини за умов постійного заданого дебіту і постійної заданої депресії тиску , де позначено р_к – постійний початковий тиск у пласті; р_с – тиск на вибої свердловини; - радіус зони поширення лійки депресії тиску на момент часу t після пуску свердловини. Оскільки радіус збільшується з часом t, то фільтраційний опір змінний у часі і зростає.

Для цих випадків можна записати зв’язок між дебітом і депресією тиску в такому вигляді:

; (9.15)

, (9.16)

а також за змінних дебіту Q_t i депресії тиску

, (9.17)

де – функція продуктивності свердловини або функція припливу (монотонно згасає в часі); – функція депресії тиску (монотонно зростає в часі); – функція часу.

Зазначимо, що для умов пружної фільтрації будувати індикаторну діаграму не можна, так як параметри фільтрації змінні в часі, а функції і є в якійсь мірі аналогом коефіцієнта продуктивності, але останній має сенс тільки стосовно усталеної фільтрації.

В обмеженому відкритому пласті, коли на межі підтримується постійний тиск р_к, лійка депресії тиску з часом наближається до усталеного стану (див. рис. 9.3, 9.4), як і вибійний тиск р_с чи дебіт Q.

У круговому замкнутому пласті за відбору нафти з постійним дебітом через деякий час має місце постійне падіння тиску у всьому пласті, в тому числі і на його межі (див. рис. 9.5), а за відбору нафти з постійною депресією тиску – зменшується дебіт свердловини (див. рис. 9.6).

Стосовно до розглянутих умов обчислимо пружний запас пласта. Оскільки тиск у кожній точці пласта різний, то пружний запас записуємо так:

, (9.17)

де – середнє зниження тиску в пласті; – середньозважений за деяким об’ємом пласта тиск.

В умовах пружноводонапірного режиму, коли на межі підтримується постійний тиск р_к (див. рис. 9.3, 9.4), розподіл тиску за наближається до усталеного стану згідно з логарифмічною залежністю, то середній тиск (див. підрозд. 4.3)

, (9.18)

а тоді пружний запас пласта

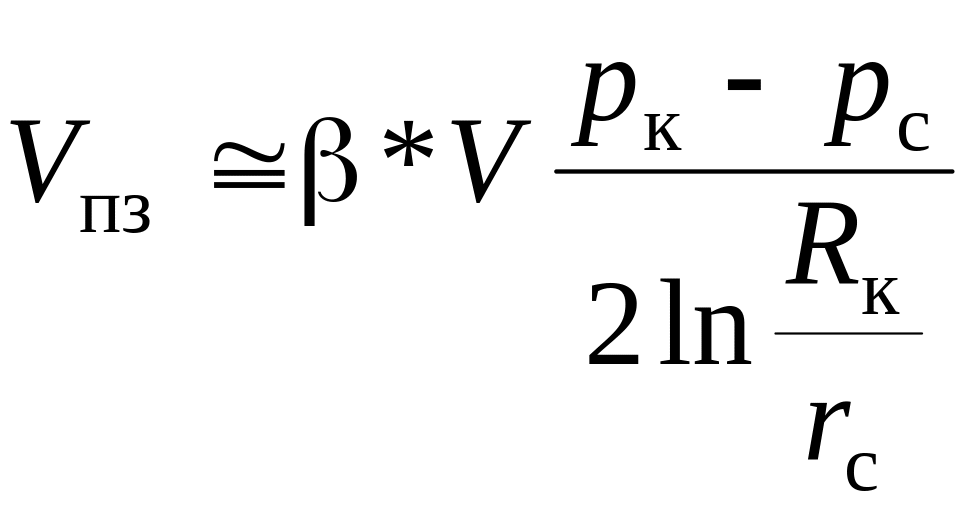. (9.19)

Якщо , то похибка обчислень за формулою (9.19) не перевищує 1%.

В умовах замкнуто-пружного режиму (див. рис. 9.5, 9.6) середній тиск залежить від дебіту Q, а конкретніше від відібраного (нагромадженого) об’єму рідини

, (9.20)

звідки

. (9.21)

Оскільки зміна нагромадженого об’єму дорівнює зміні пружного запасу пласта за проміжок часу dt, то диференціюючи рівняння (9.17) і прирівнюючи до рівняння (9.21), одержуємо диференціальне рівняння виснаження закритого пласта на замкнуто-пружному режимі:

, (9.22)

або

. (9.23)

За умови нагромаджений відбір згідно з рівнянням (9.20) лінійно зростає в часі ( ), згідно з рівнянням (9.23), а тоді середній тиск у пласті зменшується в часі за лінійним законом, тобто

. (9.24)

Формулою (9.24) можна користуватися доти, доки вибійний тиск р_с не стане таким, що дорівнює тиску насичення нафти газом р_нас.

За умови внаслідок виснаження енергії пружності пласта середній тиск , тобто коли , тоді пружний запас закритого пласта на замкнуто пружному режимі згідно з рівнянням (9.17)

. (9.25)

Очевидно, що пружний запас на замкнуто-пружному режимі за формулою (9.25) є більшим від пружного запасу на пружноводонапірному режимі за формулою (9.19), але в другому випадку нафта ще буде витіснятися до свердловин крайовою водою (за рахунок енергій пружності і напору крайової води). У першому випадку слід переходити на режим розчиненого газу. В обох випадках найбільші величини пружного запасу нафти отримуються за умови рівності вибійного тиску і тиску насичення нафти газом , тобто .