8.3 Плоско-радіальна фільтрація ідеального газу за законом Дарсі

Розглянемо фільтрацію до свердловини, концентрично розміщеної в круговому пласті.

Розподіл функції Лейбензона за аналогією описується формулою:

, (8.29)

а розподіл тиску газу з використанням виразу (8.10) звідси отримуємо у вигляді:

. (8.30)

У даному випадку лійка депресії тиску значно крутіша, ніж у разі фільтрації нестисливої рідини (рис. 8.1).

Градієнт функції Лейбензона із формули (8.29)

(8.31)

або, аналогічно переходячи до тиску,

, (8.32)

звідки градієнт тиску

. (8.33)

Об’ємна швидкість фільтрації за тиску р в будь-якій точці пласта

. (8.34)

Дебіт газової свердловини в разі припливу ідеального газу за законом Дарсі за аналогією описуємо формулою:

, (8.35)

звідки отримуємо

. (8.36)

Об’ємну витрату газу необхідно також звести до атмосферної (нормальної 273,15 К чи стандартної 293,15 К) температури, використовуючи закон Шарля

або , (8.37)

тобто витрату Q₀ слід помножити на температурну поправку

, (8.38)

де – об’ємна витрата газу за атмосферних (стандартних чи нормальних) умов, оскільки – об’ємна витрата газу за умов атмосферного тиску і плас­тової температури; , Т_пл – температури відповідно атмосферна і пластова.

Індикаторна діаграма в разі фільтрації газу будується в координатах . У даному випадку вона представлена прямою лінією.

Середній тиск газу в пласті знайдемо, взявши об’єм пор пласта , , тобто

. (8.39)

Інтеграл у рівнянні (8.39) не виражається в кінцевому вигляді. Якщо підінтегральний вираз розкласти в ряд, утримати два перших члени ряду й нехтувати членами, що містять через їх малу величину, то можна одержати наближену формулу:

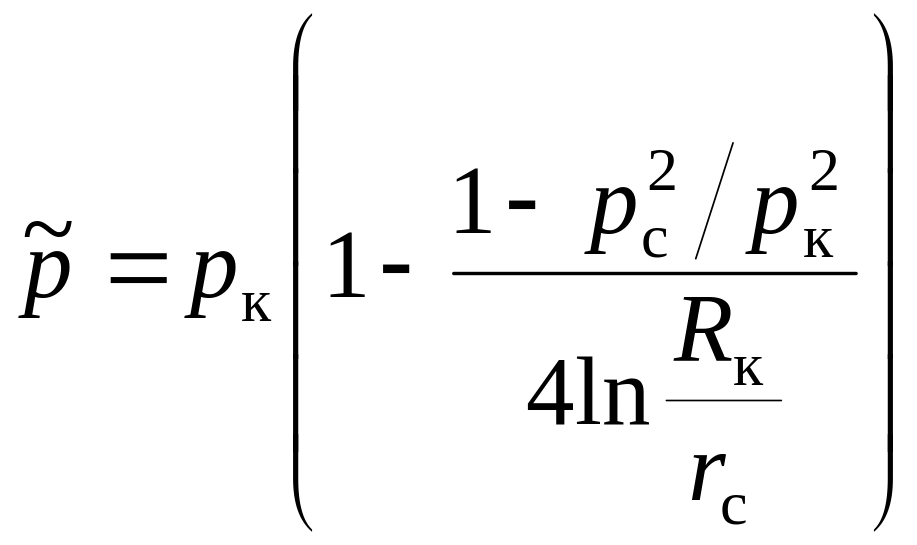. (8.40)

Розрахунки за рівняннями (8.39) чи (8.40) показують, що середній тиск у круговому пласті близький до контурного тиску, тобто

, (8.41)

що фізично пояснюється великою кривиною лійки депресії тиску.

Цей висновок щодо близькості тисків має важливе практичне значення, оскільки заміна середнього тиску контурним тиском р_к значно спрощує розрахунки процесів розробки газових покладів.

8.4 Плоско-радіальна фільтрація ідеального газу за двочленним законом

Закон Дарсі під час фільтрації газу до свердловини в більшості випадків порушується, особливо за великих дебітів. У таких випадках фільтрацію звичайно описують двочленною формулою:

. (8.42)

Формули розподілу тиску і дебіту газової свердловини одержимо, безпосередньо інтегруючи рівняння (8.42).

Попередньо записуємо:

; . (8.43)

Тоді, підставляючи  і ν у рівняння (8.42), маємо:

. (8.44)

Скорочуючи, розділяючи змінні й інтегруючи, знаходимо рівняння розподілу тиску:

; (8.45)

; (8.46)

; (8.47)

. (8.48)

Зіставляючи формули (8.30) і (8.48), доходимо висновку, що в разі порушення закону Дарсі лійка депресії тиску ще крутіша. Враховуючи велику кривину лійки депресії, ще раз переконуємося в справедливості припущення про ізотермічність процесу фільтрації газу, оскільки основна зміна температури внаслідок дросельного ефекту відбувається в найближчій околиці свердловини.

Оскільки для , то з рівняння (8.47) одержуємо формулу дебіту газової свердловини в разі припливу ідеального газу за двочленним законом:

(8.49)

або

, (8.50)

де коефіцієнти фільтраційного опору

; . (8.51)

Індикаторна лінія згідно з формулою (8.50) являє собою параболу з опуклістю до осі дебітів (рис. 8.2, а).

Коефіцієнти А і В визначають за даними газодинамічного дослідження свердловини на усталених режимах, записуючи формулу (8.50) у вигляді:

, (8.52)

де А знаходять аналітично з використанням ПЕОМ чи графічно як відрізок на осі ординат, а В – як тангенс кута  нахилу прямої (рис. 8.2, б). Тут також доцільно дебіт Q₀ помножити на температурну поправку .

Коефіцієнти А і В можна розрахувати, наприклад, за формулами згідно з методом найменших квадратів, тобто

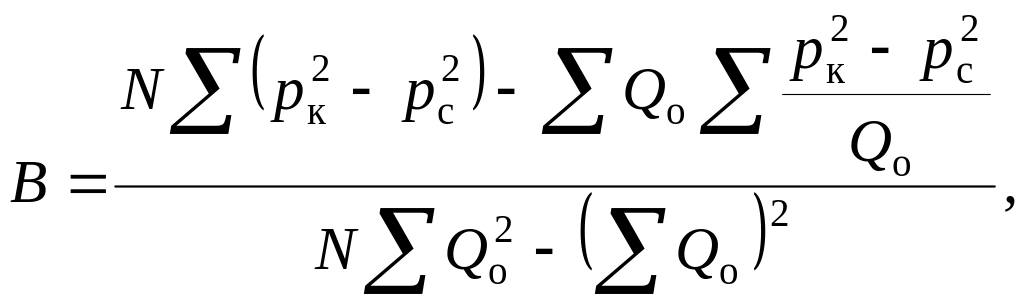
де N – кількість режимних точок на індикаторній діаграмі, а суми визначають для всіх виміряних значин і Q_o.

За знайденими значинами коефіцієнтів А і В визначають параметри пласта, наприклад коефіцієнт гідропровідності (точніше коефіцієнт газопровідності)

(8.53)

і коефіцієнт макрошорсткості

. (8.54)