7.2 Теоретичні дослідження припливу до гідродинамічно недосконалих свердловин за ступенем розкриття пласта

Строгі аналітичні розв’язки задачі про приплив рідини до гідродинамічно недосконалих свердловин наштовхуються на великі (в більшості нездоланні) труднощі. Цією задачею займалося багато дослідників. Найкращі результати одержано шляхом використання методів стоків і джерел, відображення і суперпозиції.

Припустимо спочатку, що свердловина розкрила тільки покрівлю продуктивного пласта, який має дуже велику товщину. Можна вважати, що вибій свердловини має форму півсфери радіусом r_с, продуктивний пласт – необмежену товщину (h → ∞), а потік тоді є сферично радіальним, а це відповідає найбільш яскраво вираженому випадку недосконалості свердловини за ступенем розкриття пласта.

Аналогічно випадку плоско-радіального потоку, використовуючи закон Дарсі і рівності , , записуємо умову нерозривності сферично-радіального фільтраційного потоку:

(7.12)

або

(7.13)

де – площа фільтрації (площа поверхні півсфери).

Інтегруючи двічі, отримуємо загальний розв’язок:

;

;

, (7.14)

а відтак, за граничних умов

(7.15)

маємо формулу розподілу тиску в пласті

(7.16)

і формулу градієнта тиску

(7.17)

Таблиця 7.1 – Відповідність параметрів , с і r_сз між собою для r_c=0,1 м, R_к=300 м.

	с	rсз			с	rсз
0 0,1 0,2 0,3 0,4 0,5 0,6	∞ 72,057 32,025 18,682 12,010 8,006 5,338	0 0 1,235·10-15 7,704·10-10 6,086·10-7 3,333·10-5 4,807·10-4		0,7 0,8 0,9 1,0 1,1 1,2 1,3	3,431 2,002 0,890 0 -0,728 -1,334 -1,848	3,234·10-3 0,014 0,041 0,100 0,207 0,380 0,634

Використовуючи вираз (7.17), отримуємо формулу дебіту півсферичної свердловини

;

(7.18)

або

, (7.19)

так як .

Задача 7.1. Визначити у скільки разів дебіт Q_p вертикальної циліндричної свердловини у випадку плоско-радіальної фільтрації є більшим від дебіту півсферичної Q_c у випадку сферично-радіальної фільтрації, якщо взяти r_с=0,1 м, R_к=200 м, h=50 м.

Розв’язування. Візьмемо відношення цих дебітів за формулами Дюпюї і (7.18), тобто

Відповідь: Q_p / Q_c = 65,75.

Н. К. Гирінський прийняв, що свердловина розкрила пласт необмеженої товщини (h → ∞) на глибину b (це рівнозначно умові ), і дістав наближену формулу:

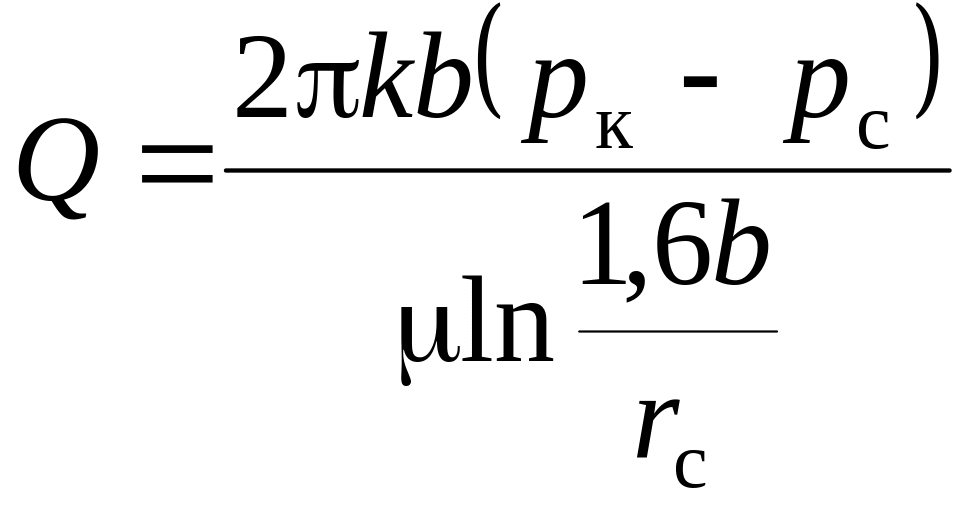. (7.20)

Досить задовільну практичним вимогам точність забезпечує формула І. Козені:

. (7.21)

М. М. Глоговський для розв’язування задачі застосував метод рядів Бесселя, але розв’язок отримано дуже складним у вигляді нескінченної суми функцій Бесселя.

Найточнішу формулу дебіту гідродинамічно недосконалої свердловини за ступенем розкриття пласта з донним припливом вивів М.Маскет. Для розв’язування задачі вздовж осі свердловини він розмістив уявну лінію, яка поглинає рідину і кожний елемент якої є просторовим стоком. Розв’язок одержував за граничних умов: покрівля і підошва пласта непроникні, а тиск для , для . Такі умови задовільняються нескінченним відображенням цих просторових стоків у покрівлі й підошві пласта та відповідним вибором змінної питомої витрати (інтенсивності) стоків вздовж осі свердловини, щоб виконати умову постійності тиску на поверхні свердловини. Відтак використовуючи метод суперпозиції дійсних і відображених стоків, М. Маскет дістав формулу дебіту гідродинамічно недосконалої свердловини за ступенем розкриття пласта:

, (7.22)

де – коефіцієнт фільтраційного опору; –відносне розкриття пласта; – функція відносного розкриття; – інтеграл Ейлера другого роду, який називається ще гамма-функцією (числові значини її подано в математичних довідниках); п – число (аргумент гамма-функції); х – довільна змінна.

Для експрес-обчислень можна використати графік , що зображений на рис. 7.2.

Якщо відносне розкриття пласта , тобто пласт розкритий свердловиною на всю товщину, то і формула Маскета перетворюється на формулу Дюпюї для плоско-радіального потоку.

Зіставляючи між собою формули (7.7) і (7.22), із формули Маскета отримаємо аналітичну формулу для визначення коефіцієнта додаткового фільтраційного опору, який зумовлено гідродинамічною недосконалістю свердловини за ступенем розкриття пласта:

(7.23)

Задача 7.2. Розрахувати зміну дебіту Q гідродинамічно недосконалої свердловини в залежності від ступеня розкриття пласта (тривимірний рух) і дебіт Q_р досконалої свердловини у випадку плоско-радіального потоку (двовимірний, плоский рух) у залежності від розкритої товщини пласта для товщини пласта 20; 40 і 80 м, а також їх відносну зміну . Відомо: k = 50·10^-15 м²; μ=10^-3 Па·с; r_с=0,1 м; R_к=200 м; Δр=10⁶ Па.

Розв’язування. Дебіт Q визначаємо за формулою Маскета (7.22), а дебіт Q_р – за формулою Дюпюї (7.4), в якій замість h беремо . Наприклад, для h = 20 м і маємо:

м³/с;

м³/с;

Результати розрахунку показано на рис. 7.3 і 7.4. Із рисунків видно, що вертикальна складова припливу може бути дуже великою за малих значин відносного розкриття пласта, тому нехтування нею призведе до значних похибок у розрахунку дебіту.

Відношення дебіту гідродинамічно недосконалої свердловини за ступенем розкриття пласта до дебіту досконалої свердловини (коефіцієнт досконалості δ) в залежності від товщини пласта за різних ступенів розкриття показано на рис.7.5. Звідси видно, що коефіцієнт досконалості свердловини різко зменшується до товщини порядка 30 м, тобто за більших товщин вертикальна складова припливу практично відсутня.

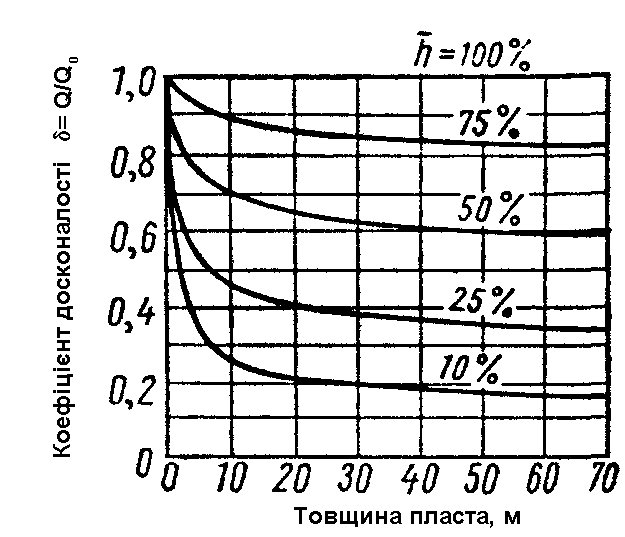
Рис. 7.5 – Зміна коефіцієнта досконалості δ із зміною товщини пласта (Q – дебіт недосконалої свердловини; Q_доск – дебіт досконалої свердловини; радіус свердловини r_c=7,5 см; радіус зовнішнього контура R_к=200 м)

М. Маскет ще вивів рівняння розподілу тиску в пласті стосовно випадку припливу рідини до недосконалої свердловини за ступенем розкриття пласта. Розподіл тиску для показано на рис. 7.6. З рис. 7.6 видно, якщо , то ізобари практично збігаються з ізобарами у випадку плоско-радіального руху (досконала свердловина). Тобто для подібних розрахунків припливу до недосконалих свердловин можна застосувати ідею (метод) “зрощування (зшивання) фільтраційного потоку” – плоско-радіального та викривленого.

На цій основі І.А. Чарний область фільтрації розділив на дві зони – плоско-радіального (для ) та сферично-радіального (для , , причому за результатами експериментів ) потоків і запропонував простішу формулу дебіту гідродинамічно недосконалої свердловини за ступенем розкриття пласта:

, (7.24)

допустивши, що .

Задача 7.3. Вважаючи формулу Маскета дебіту свердловини Q_м (7.22) точною (правильніше, найбільш точною), зіставити з нею формули дебіту напівсферичної свердловини Q_с (7.18), Гирінського Q_г (7.20), Козені Q_к (7.21) і Чарного Q_ч (7.24) за різного розкриття продуктивного пласта в залежності від ступеня розкриття пласта . Відомо: r_с=0,1 м; R_к=300 м; h=40 м.

Розв’язування. Беремо відношення Q_с/Q_м, Q_г/Q_м, Q_к/Q_м і Q_ч/Q_м, при цьому у формулах Гирінського і Чарного b= h. Результати розрахунку показано на рис.7.7, звідки бачимо наближеність ряду формул.

М. Маскет дослідив також вплив анізотропії пласта за проникністю на приплив до недосконалої свердловини за ступенем розкриття пласта. Під анізотропією пласта розуміють неоднаковість його проникності в різних напрямах.

Для характеристики фільтраційних властивостей анізотропного пористого середовища використовують аффінний симетричний тензор коефіцієнта проникності другого рангу , який має таку матрицю:

.

Тоді лінійний закон фільтрації в анізотропному середовищі записують у вигляді:

(7.25)

Із такого запису закону фільтрації випливає, що вектор швидкості фільтрації в анізотропному середовищі може не співпадати за напрямом з вектором градієнта тиску grad p, а співпадання можливе тільки в тому випадку, коли за осі координат вибрати головні осі симетричного тензора коефіцієнта проникності (при цьому матриця тензора коефіцієнта проникності має діагональний вигляд). Для симетричного аффінного тензора коефіцієнта проникності існують три ортогональні головні напрями і три головні значини коефіцієнтів проникностей k₁, k₂, k₃.

Отже, координатні осі скеровують так, щоб вони співпадали з головними значинами коефіцієнтів проникностей, тоді вздовж кожної із осей координат коефіцієнти проникності залишаються постійним, ак закон Дарсі можна записати для анізотропного пористого пласта в такому вигляді:

; ; , (7.26)

де k_x, k_y, k_z – коефіцієнти проникності вздовж відповідних координатних осей (Оx, Оy, Оz); ρ – густина рідини; g – прискорення вільного падіння. Оскільки пласт залягає горизонтально, але розглядається фільтрація вздовж вертикальної координати z, то враховано зміну тиску за рахунок стовпа рідини доданком ρg.

Підставляючи рівняння (7.26) у рівняння нерозривності усталеного потоку нестисливої рідини

, (7.27)

отримуємо диференціальне рівняння усталеної фільтрації нестисливої рідини в анізотропному за проникністю пласті:

. (7.28)

Такі задачі розв’язують методом ізотропізуючої деформації простору, перетворюючи систему координат (x, y, z) у нову систему координат (x₁, y₁, z₁) за формулами:

; ; , (7.29)

у результаті рівняння (7.28) набуває канонічної форми рівняння Лапласа:

, (7.30)

де с – постійна величина, яка може бути вибрана довільно, якщо розв’язок містить тільки відношення лінійних величин.

Якщо , то (7.30) можна записати

(7.31)

або, замінюючи змінну

, (7.32)

де – коефіцієнт анізотропії пласта за проникністю, причому , оскільки коефіцієнт проникності k_z може набувати значин і ; k_г – коефіцієнт проникності в горизонтальному напрямку.

Отже, для врахування анізотропії пласта за проникністю треба вертикальні лінійні розміри зменшити в  разів. Аналогічно можна показати, що для врахування анізотропії допускається вертикальні лінійні розміри залишити без зміни, а горизонтальні – збільшити в  разів.

На рис. 7.8 показано відношення дебіту Q₁ недосконалої свердловини в ізотропному пласті до дебіту Q_ недосконалої свердловини в гранично анізотропному пласті , коли коефіцієнт проникності k_z вздовж вертикальної осі z дорівнює нулю, залежно від відносного розкриття пласта (взято h = 37,5 м; r_с = 0,075 м; R_к = 152,5 м). Так, за рахунок вертикальних складових швидкостей фільтрації для дебіт підвищується на 50 %, а для – більш як на 75 %, тобто дебіт зростає різкіше, ніж глибина розкриття (за малих значин розкриття), але сповільнено в міру того, як відносна глибина розкриття сягає одиниці. У випадку великих значин відносного розкриття анізотропію пласта за проникністю можна не враховувати. Дебіт свердловини інтенсивно зростає залежно від збільшення за малих значин цього відношення і повільно змінюється, коли (рис. 7.9).

Рис. 7.9 – Продуктивність свердловин, недосконалих за ступенем розкриття пласта, в залежності від відношення коефіцієнтів проникностей k_z / k ( – індекс продуктивності; товщина пласта h = 38 м; радіус свердловини r_c = 7,5 см; радіус зовнішнього контура R_к = 150 м; динамічний коефіцієнт в’язкості μ = 1 мПа·с)

Звідси випливає практичний висновок, що поки коефіцієнт проникності k_z не складає значної частки коефіцієнта k, то анізотропія проникності зумовлює значне зниження дебіту, а, значить, її слід враховувати в розрахунках.