5.2 Усталена фільтрація нестисливої рідини в неоднорідних пористих пластах за законом Дарсі

Усі реальні нафтові та газові пласти неоднорідні за своєю геологічною будовою і властивостями, що викликано умовами осадоутворення та подальшого перетворення порід. Під неоднорідністю розуміють властивість пласта-колектора, яка зумовлена зміною його структурно-фаціальних і літологічних характеристик. З позицій фільтрації важливою є неоднорідність за проникністю. У разі хаотичної і незначної локальної зміни проникності пласт вважають у середньому однорідним. Якщо вдається виділити значні області пласта з різними проникностями, то пласт називають неоднорідним, виділяючи в основному шарову та зональну неоднорідність.

Розглянемо особливості фільтрації в таких пластах на прикладі плоско-радіального потоку.

Шарова неоднорідність. У цьому випадку маємо багатошаровий пласт (рис. 5.4). У межах кожного шару (пропластка) проникність усюди однакова, а на межі сусідніх пропластків змінюється стрибком.

Оскільки розподіл тиску в однорідному пласті (точніше, в однорідному пропластку) не залежить від проникності , градієнт тиску також однаковий в усіх пропластках , то для будь-якої одної значини координати r тиск у всіх пропластках буде однаковим, а отже, перетікання рідини між цими пропластками не відбуватиметься (нагадаємо, що йдеться про зведені тиски). Тоді витрата рідини через весь пласт дорівнюватиме сумі витрат через кожний пропласток. Наприклад, для двох пропластків формулу дебіту свердловини в шарово-неоднорідному пласті можна записати так:

або

, (5.15)

де k_i, h_i – коефіцієнт проникності і товщина i-го пропластка ( i = 1; 2).

Якщо ввести поняття середнього коефіцієнта проникності усього пласта, то дебіт свердловини за формулою Дюпюї:

, (5.16)

а прирівнявши дебіти за цими формулами, матимемо вираз для середнього коефіцієнта проникності шарово-неоднорідного пласта:

(5.17)

або у випадку n пропластків

. (5.18)

Отже, для розрахунків фільтрації в неоднорідних багатошарових пластах можна використати формули для однорідного пласта, тільки замість коефіцієнта проникності k необхідно підставити середній коефіцієнт проникності .

Разом з тим треба пам’ятати, що градієнт тиску, розподіл тиску і п’єзометрична лінія однакові в усіх пропластках, бо не залежать від коефіцієнта проникності, а швидкість фільтрації і час руху частинок рідини відповідно прямо і обернено пропорційні коефіцієнтам проникності пропластків, тобто у високопроникних пропластках кожна частинка рідини рухається швидше, ніж у малопроникних пропластках.

У разі прямолінійно-паралельного потоку формула (5.18) також справедлива (пропонуємо читачеві самостійно в цьому переконатися).

Зонально-неоднорідний пласт. Такий пласт є розчленованим на зони (області), у кожній з яких проникність усюди однакова, а на переході через межу двох сусідніх зон змінюється стрибком.

Розглянемо круговий пласт з концентричною свердловиною, навколо якої виділяється зона з іншим коефіцієнтом проникності k₁, ніж коефіцієнт проникності k₂ решти пласта (рис. 5.5). Межа поділу зон перпендикулярна до лінії течії, тобто є коловою з радіусом R.

Такі задачі часто розв’язують на основі граничної умови, коли на межі поділу зон для r = R згідно із законом нерозривності потоку швидкості фільтрації в обох зонах мають бути однаковими, тобто

, (5.19)

або

. (5.20)

Розподіл тиску в кожній зоні описується відомими нам формулами:

; (5.21)

, (5.22)

де p_р – тиск на межі поділу зон з різними проникностями.

Продиференціювавши рівняння (5.21) і (5.22) і підставивши результат у вираз (5.20), дістанемо вираз для невідомого тиску на межі поділу:

. (5.23)

Тоді формули розподілу тиску в зонах з різними проникностями набувають вигляду:

; (5.24)

. (5.25)

Лійки депресії тиску в такому пласті показано на рис. 5.5 за різних співвідношень коефіцієнтів проникностей k₁ і k₂. Наприклад, якщо то

,

тоді п’єзометрична лінія має лежати вище лінії для k₁ = k₂.

Продиференціювавши формулу (5.23) або (5.24) і підставивши результат відповідно у вираз для або , записуємо рівняння швидкості фільтрації в усьому зонально-неоднорідному пласті

(5.26)

і формулу дебіту свердловини в зонально-неоднорідному пласті

. (5.27)

Зазначимо, що в разі усталеного руху нестисливої рідини витрата є постійною в кожній зоні. Тоді, записуючи її вираз для кожної зони згідно з формулою Дюпюї і використовуючи властивість похідних пропорцій щодо суми її членів де a, b, c, d – члени пропорції), легко дістанемо рівняння дебіту (5.27). Таке ж рівняння (5.27) отримаємо і тоді, коли запишемо, що загальна втрата тиску дорівнює сумі втрат тиску в кожній зоні, тобто або , де втрати тиску виражаємо із формули Дюпюї для кожної зони.

Аналогічно попередньому введемо поняття середнього коефіцієнта проникності пласта , тоді дебіт свердловини в зонально-неоднорідному пласті опишеться формулою Дюпюї для однорідного пласта, тобто

. (5.28)

Прирівнюючи формули (5.27) і (5.28) отримуємо вираз середнього коефіцієнта проникності зонально-неоднорідного пласта:

(5.29)

або у випадку наявності n зон з різними проникностями

, (5.30)

причому R_і-1= R₀ = r_с для i =1 та R_і = R_к для i = n.

Якщо задано закон плавної зміни коефіцієнта проникності k(r), то дебіт свердловини можемо записати так:

, (5.31)

звідки аналогічно, середній коефіцієнт проникності

(5.32)

Проникність зони пласта поблизу стінки свердловини (привибійна зона пласта), як правило, відрізняється від проникності решти пласта. Ця зміна зумовлена забрудненням (кольматацією) пор під час буріння свердловини (фільтратом і дисперсною фазою бурового розчину) і під час експлуатації (відкладами парафіну, мінеральних солей) або цілеспрямованим використанням методів інтенсифікації продуктивності свердловини (солянокислотне оброблення і т. ін.). Для оцінки впливу такої зміни проникності в привибійній зоні внаслідок кольматації чи інтенсифікації на дебіт свердловини зіставляють дебіт Q зонально неоднорідного пласта з дебітом Q₂ однорідного пласта за коефіцієнта проникності k_2, тобто

, (5.33)

де – відношення коефіцієнтів проникностей.

Звідси випливають важливі практичні висновки (рис. 5.6):

1) зменшення коефіцієнта проникності привибійної зони більше впливає на дебіт свердловини, ніж збільшення його в однакову кількість разів і призводить до різкого падіння дебіту, навіть за малих величин радіуса R зони погіршення проникності;

2) у разі фільтрації за законом Дарсі збільшувати коефіцієнт проникності в привибійній зоні більше як у 20 разів недоцільно, оскільки дебіт майже не зростає;

3) оскільки лійка депресії тиску в разі фільтрації за нелінійним законом більш крута, ніж у разі фільтрації за законом Дарсі (більша частка втрати депресії тиску в привибійній зоні), то збільшення коефіцієнта проникності в привибійній зоні веде до значнішого приросту дебіту, якщо рідина фільтрується за нелінійним законом.

За наявності декількох зон з різною проникністю, наприклад, через накладання процесів глинистої і парафінової кольматації, через зниження проникності внаслідок проникання в пласт фільтрату бурового розчину в ході буріння свердловини чи рідини глушіння під час її ремонту, через збільшення проникності внаслідок застосування методу солянокислотного оброблення і т. п., дебіт свердловини записується аналогічно:

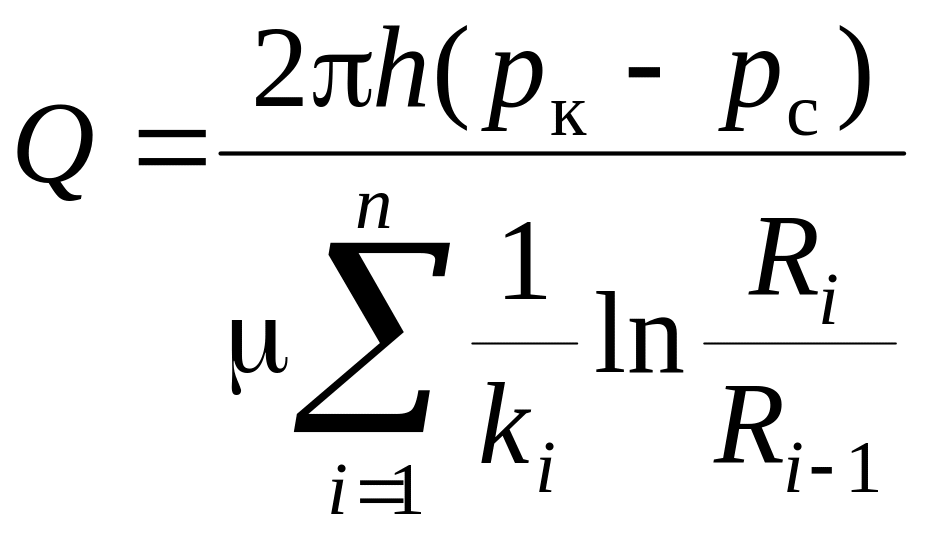, (5.34)

а відношення дебітів

, (5.35)

де – дебіт свердловини за початкової, непорушеної природної проникності пласта (іншими словами, у віддаленій від свердловини зоні пласта), яка характеризується коефіцієнтом проникності .

Ці формули дають змогу оцінити негативний вплив кольматації або технологічну ефективність (приріст дебіту) солянокислотного оброблення (СКО). Для оцінки ефективності СКО слід задати величину коефіцієнта проникності в зоні оброблення (за лабораторними даними) або наближено розрахувати її за величиною збільшення коефіцієнта пористості внаслідок розчинення карбонатного цементу породи в соляній кислоті, використовуючи статистичний зв’язок між коефіцієнтами пористості і проникності (див. гл. 1). Нагадаємо, що об’ємний вміст карбонатів (CaCO₃, MgCO₃) визначається в лабораторії відносно до об’єму твердої частини (скелету) гірської породи.

У випадку одновимірного потоку в зонально-неоднорідному пласті до галереї п’єзометричні лінії представлені ламаними прямими лініями (рис. 5.7), а середній коефіцієнт проникності виражається формулою:

(5.36)

або

, (5.37)

де l_i – довжина i -ї зони з коефіцієнтом проникності k_i.

Розподіл тиску в кожній зоні описується лінійною залежністю, а градієнт тиску в межах кожної зони постійний, але різний у різних зонах. Витрата рідини (дебіт) Q і швидкість фільтрації постійні в будь-якому перерізі потоку ( ), а дійсні середні швидкості руху частинок рідини в різних зонах пласта різні (обернено пропорційні коефіцієнтам пористості), оскільки, як правило, чим більший коефіцієнт проникності, тим більший коефіцієнт пористості.

Такий потік може мати місце також у вертикальному напрямку впоперек напластування гірських порід різного літологічного складу з різними коефіцієнтами проникності. Зрозуміло, якщо зустрічається шар, коефіцієнт проникності якого дорівнює нулю (наприклад, шар глини), то фільтрація у вертикальному напрямку відсутня ( ), а непроникний шар є гідродинамічним екраном.

Детально дослідження прямолінійно-паралельного потоку в зонально неоднорідному пласті пропонуємо читачеві здійснити самостійно.