4.3 Усталена плоско-радіальна фільтрація нестисливої рідини до свердловини в пористому пласті за законом Дарсі

У випадку плоско-радіальної фільтрації до гідродинамічно досконалої свердловини із рівняння (4.3) маємо (див. підрозд. 2.1):

. (4.21)

З метою спрощення задачі доцільно перейти від декартових координат до полярних, оскільки внаслідок осьової симетрії потік залежить тільки від радіуса-вектора (рис. 4.4, б)

(4.22)

і не залежить від полярного кута.

Виражаючи і через r, не важко одержати рівняння Лапласа в полярних координатах для плоско-радіального потоку, а саме:

. (4.23)

Граничні умови

(4.24)

де p_c, p_к – тиски відповідно на контурі свердловини (вибійний тиск) і на контурі живлення пласта (контурний або пластовий тиск); r_c, R_к – радіуси відповідно свердловини та контура живлення пласта.

Задача повністю поставлена. Розв’яжемо її. Загальний розв’язок отримуємо так:

. (4.25)

Рівняння (4.25) є загальним розв’язком, в якому с₁ та с₂ – постійні інтегрування.

Зауважимо, що загальний розв’язок (4.25) можна отримати простішим шляхом, якщо використати рівняння нерозривності фільтраційного потоку

або за = const

,

або

,

де F – площа фільтрації, F = 2πrh (це бокова поверхня циліндра).

Оскільки довжина шляху фільтрації l = R_к – r (див. рис. 4.4, б), звідси dl = - dr, то закон Дарсі (1.12) для плоско-радіальної фільтрації записується у вигляді формули:

. (4.26)

У випадку усталеного фільтраційного потоку нестисливої рідини об’ємна витрата Q є сталою величиною вздовж шляху фільтрації, то рівняння нерозривності можна записати

або

або за

(4.27)

Оскільки похідна від постійної величини дорівнює нулю, тобто

то, інтегруючи двічі рівняння (4.27), одержуємо загальний розв’язок (4.25).

Постійні інтегрування с₁ і с₂ визначаємо із граничних умов (4.24), тобто

,

звідки

(4.28)

або

.

(Надалі під логарифмом з метою простішого запам’ятовування і зіставлення формул писатимемо відношення більшого радіуса до меншого). Підставляючи знайдені постійні с₁ і с₂ у загальний розв’язок (4.25), дістаємо як частковий розв’язок рівняння розподілу тиску в пласті (рівняння п’єзометричної лінії):

, (4.29)

або

. (4.30)

Залежності (4.29) чи (4.30) є логарифмічною кривою лінією, яка дуже крута поблизу свердловини, а відтак виположується і перетинає горизонтальну лінію початкового тиску p_к у пласті за r = R_к (див. рис. 4.4, а). Більший нахил логарифмічної лінії біля стінки свердловини свідчить про те, що тут витрачається основна частина депресії тиску на пласт, тобто p = p_к – p_c.

Під час обертання логарифмічної п’єзометричної лінії навколо осі свердловини одержуємо поверхню, яку називають лійкою депресії тиску (депресійною лійкою).

Із рівняння (4.29) випливає, що тиск однаковий в усіх тих точках пласта, для яких

(4.31)

або в декартових координатах

.

Вираз (4.31) є рівнянням ізобар (ліній однакового тиску). Ізобари являють собою концентричні відносно осі свердловини кола, які перпендикудярні до ліній течії. Будується гідродинамічне поле так: перехід від радіуса до радіуса здійснюється в геометричній прогресії, щоб забезпечити перехід від ізобари до ізобари в арифметичній прогресії (див. рис. 4.4, б).

Диференціюючи рівняння (4.29), маємо вираз градієнта тиску

. (4.32)

Тоді, підставляючи вираз (4.32) у формулу закона Дарсі (4.20), дістаємо вираз швидкості фільтрації:

. (4.33)

Помноживши вираз (4.33) на площу фільтрації F = 2rh, маємо формулу дебіту свердловини (формулу Дюпюї), або рівняння припливу рідини:

(4.34)

де h – товщина продуктивного пласта. При цьому об’ємна витрата нестисливої рідини усталеного плоско-радіального потоку вздовж лінії течії (вздовж радіуса r) не змінюється (рис. 4.5).

Рис. 4.5 – Зміна характеристик усталеного плоско-радіального фільтраційного потоку вздовж лінії течії (вздовж осі Оr)

Зауважимо, що формулу Дюпюї можна також дістати безпосереднім інтегруванням рівняння закону Дарсі (4.26), взявши

, (4.35)

тобто

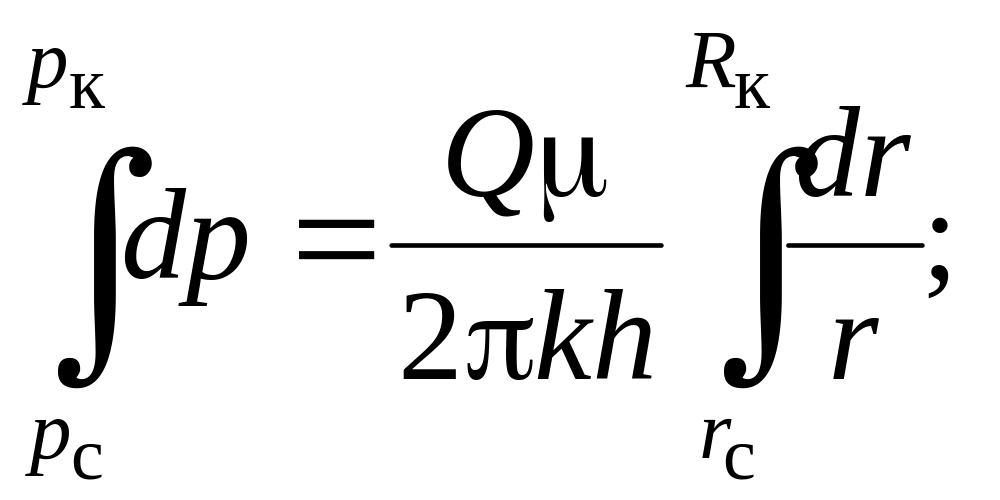
звідки виходить (4.34).

Із формули (4.34) маємо

тому рівняння розподілу тиску в пласті (4.28) можна записати ще й так:

. (4.36)

Із рівнянь (4.32) і (4.33) видно, що і v обернено пропорційні r (гіперболічна залежність – рівнобока гіпербола), тобто з наближенням до свердловини градієнт тиску та швидкість фільтрації v зростають, сягаючи найбільших значин на стінці свердловини (див. рис. 4.5).

Логарифмічна залежність дебіту Q від радіусів R_к і r_c підкреслює, що тільки значна зміна цих параметрів може істотно вплинути на величину дебіту. Щоб збільшити дебіт Q вдвічі, відношення радіусів треба зменшити до . Це означає, що в разі R_к = const радіус r_c має збільшитися до , а в разі r_c = const радіус R_к має зменшитися до . Наприклад, для R_к = 1000 м, r_c = 0,1 м, = 10⁴, = 10^2, =10, тобто радіус свердловини має дорівнювати 1 м, або радіус контура пласта – 100 м.

Звідси випливають важливі практичні висновки:

1) невідомість точних значин R_к і r_c (на практиці їх і не вдається визначити точно) не вносить значних похибок у розрахунок дебіту;

2) практично неможливо досягнути значного збільшення дебіту за рахунок збільшення r_c (свердловини великого діаметра бурять з метою зменшення втрат тиску в її стовбурі під час руху флюїду від вибою до гирла у випадку великих дебітів);

3) формулу Дюпюї можна застосовувати не тільки у випадку наявності колових контурів живлення пласта, але й у багатьох випадках, коли контур має звивисту форму;

4) формулу Дюпюї можна застосовувати й у випадку нерівномірного розподілу тиску вздовж контура живлення пласта, розуміючи під р_к середній тиск на лінії контура живлення (аналогічно й щодо контура свердловини).

Рівняння припливу (4.34) можна записати ще й так:

, (4.37)

де К₀ – коефіцієнт продуктивності свердловини, Δр – депресія тиску, p = p_к - p_c.

Графік залежності дебіту свердловини Q від депресії тиску p називають індикаторною діаграмою (лінією). У випадку фільтрації нестисливої рідини за законом Дарсі в пористому пласті індикаторна діаграма є прямою лінією (рис. 4.3, а). Зауважимо, що індикаторну діаграму будують тільки стосовно усталеного потоку.

У розглянутій постановці, коли визначається дебіт Q за заданої депресії тиску p та відомих параметрів пласта і свeрдловини (, k, h, R_к, r_c), розв’язуєтся пряма задача підземної гідрогазомеханіки. Використовуючи індикаторну діаграму, можна розв’язувати обернену задачу, тобто визначати параметри пласта і свердловини за відомих Q і p. Величини Q і p відомі за даними гідродинамічного дослідження свердловини на усталених режимах. При цьому задають не менше як три усталені режими, що характеризуються трьома парами Q і p. Величину p визначають з використанням манометрів, а дебіт свердловини вимірюють на поверхні лічильником. Тільки необхідно виконати перерахунок до умов пласта:

, (4.38)

де b_н – об’ємний коефіцієнт рідини (нафти); Q_пов – об’ємний дебіт рідини за поверхневих (стандартних чи нормальних) умов (розгазована нафта).

Тоді будують індикаторну діаграму Q (p), за якою або графічно як тангенс кута  її нахилу до осі p, або з використанням методу найменших квадратів, або в машинній програмі системи MathCAD з використанням оператора лінійної регресії (сучасний спосіб визначення), знаходять коефіцієнт продуктивності:

. (4.39)

Знаючи K₀, розраховують коефіцієнт гідропровідності пласта (або просто кажуть гідропровідність пласта)

(4.40)

коефіцієнт плинності рідини в пористому середовищі

(4.41)

коефіцієнт проникності пласта

(4.42)

Відношення дебіту свердловини до депресії тиску p за справедливості закону Дарсі називають коефіцієнтом продуктивності свердловини К₀.

Для зіставлення різних свердловин між собою за продуктивною характеристикою визначають також питомий коефіцієнт продуктивності

. (4.43)

Іноді індикаторну діаграму будують в координатах Q та p_c (див. рис. 4.3, б). Дебіт Q_пот для p_c = 0 називають потенціальним дебітом свердловини. Зверніть увагу, що екстраполюючи на рис. 4.3, б індикаторну лінію Q(p_c) до осі тиску p_c, маємо можливість визначити тиск p_к на контурі пласта, не вдаючись до інструментального його вимірювання (цей тиск вимірюють з допомогою свердловинного манометра на вибої свердловини, яка тривалий час не працює).

Визначимо ще середній тиск у пласті (середньозважений за об’ємом)

, (4.44)

де – середній тиск у пласті; V_п – об’єм пор пласта; p – тиск у довільній точці пласта.

Об’єм пор пласта тоді з урахуванням рівняння (4.29) середній тиск

(4.45)

де 2πrdr – площа смужки довжиною 2πr і шириною dr.

Інтегруючи вираз (4.45), дістаємо

, (4.46)

або нехтуючи усіма членами, що містять (оскільки ),

. (4.47)

Розділимо рівняння (4.47) на p_к і матимемо:

. (4.48)

Нехай p_с/p_к = 0,8; R_к/r_c = 10⁴, тоді , а отже, середній тиск мало відрізняється від контурного тиску p_к.

Для визначення часу руху чаcтинок рідини використовуємо вже відомий зв’язок (1.5) між дійсною швидкістю w і швидкістю фільтрації v і записуємо:

(4.49)

(знак ’’ – ’’ поставлено тому, що із зростанням часу t радіус r зменшується – рідина рухається до свердловини).

Розділяючи змінні в рівнянні (4.49) та інтегруючи, дістаємо формулу часу руху частинок рідини, тобто

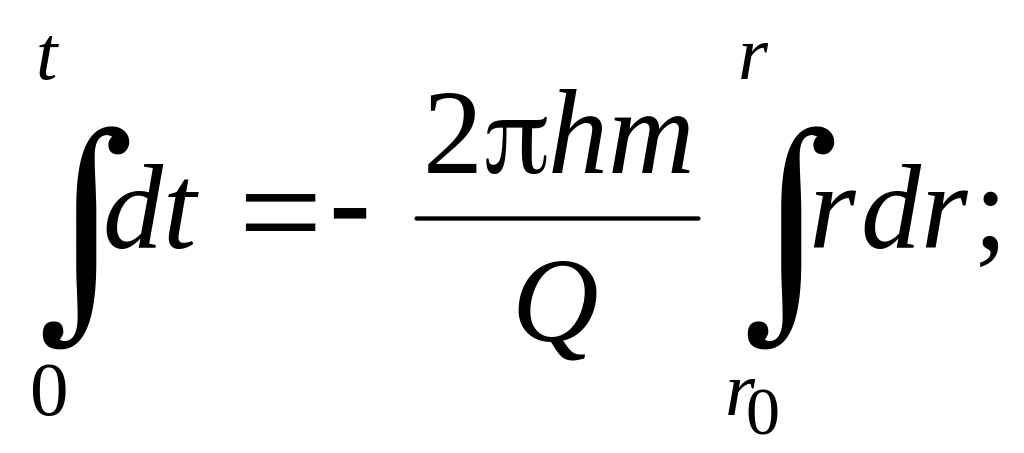
(4.50)

або з урахуванням формули Дюпюї (4.34)

, (4.51)

де r₀ – радіус будь-якої точки пласта.

Час руху частинок рідини з відстані r_o до стінки свердловини r ₌ r_с

, (4.52)

або за

, (4.53)

а повний час руху від контура живлення пласта (r₀ = R_к) до свeрдловини, чи в разі наближених розрахунків час переміщення ВНК,

, (4.54)

де – об’єм запасу нафти в пласті.

Зауважимо, що усі виведені тут формули залишаються справедливими і стосовно випадку нагнітання рідини в пласт, тобто стосовно до нагнітальної свердловини, коли р_с > р_к. А тоді у виведені формули замість депресії тиску (р_к – р_с) треба підставити репресію тиску (р_в – р_к), при цьому графік розподілу тиску (див. рис. 4.2) буде дзеркальним відображенням у горизонтальній площині щодо лінії тиску р_к = const.