Вариант №7
Задача 1. Подробно раскрыть тему: Одноканальная СМО с ожиданием (очередью). Формулы Литтла.
Задача 2. Магазин посещает в среднем 90 человек в час. Имеющийся один кассир обслуживает в среднем одного покупателя в минуту. Очередь в зал обслуживания ограничена 5 покупателями. Оценить эффективность работы СМО.
Задача 3. В систему массового обслуживания (СМО) поступает в среднем 120 заявок ед/час. Найти вероятность того, что за время 2 мин в СМО поступит ровно 3 заявки, менее 3 заявок; более 3 заявок.
Задача 4. Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие.
а) составить матрицу интенсивностей переходов;
б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;
в) найти предельное распределение
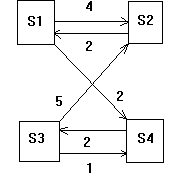
Задача 5. Рассматривается 3-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно 3. Поток заявок, поступающих в СМО, простейший с интенсивностью 6 ед/час. Среднее время обслуживания заявки равно 20 мин. Время обслуживания распределено по показательному закону. Определить относительную пропускную способность.
Вариант №8
Задача 1. Подробно раскрыть тему: Многоканальная СМО с неограниченным ожиданием (очередью).
Задача 2. Заявки на телефонные переговоры поступают с интенсивностью 1,2 заявки в минуту, а средняя продолжительность разговора по телефону составляет 2 минуты. Найти вероятность того, что в СМО за 3 минуты поступит не более 2-х заявок.
Задача 3. В систему массового обслуживания (СМО) поступает в среднем 40 заявок ед/час. Найти вероятность того, что за время 6 мин. в СМО поступит ровно 5 заявок, менее 5 заявок; более 5 заявок.
Задача 4. Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие.
а) составить матрицу интенсивностей переходов;
б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;
в) найти предельное распределение
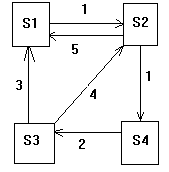
Задача 5. Рассматривается 4-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно 2. Поток заявок, поступающих в СМО, простейший с интенсивностью 4 ед/час. Среднее время обслуживания заявки равно 60 мин. Время обслуживания распределено по показательному закону. Определить среднее число заявок в очереди.
Вариант №9
Задача 1. Подробно раскрыть тему: СМО с параллельным и последовательным расположением каналов.
Задача 2. В приборе имеются два блока, работающих независимо друг от друга. Время безотказной работы определяется показательным законом. Среднее время безотказной работы 1-го блока 2 года, 2-го - 1 год. Найти вероятность того, что за 1,5 года откажут оба блока.
Задача 3. В систему массового обслуживания (СМО) поступает в среднем 30 заявок ед/час. Найти вероятность того, что за время 4 мин. в СМО поступит ровно 4 заявки, менее 4 заявок; более 4 заявок.
Задача 4. Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие.
а) составить матрицу интенсивностей переходов;
б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;
в) найти предельное распределение
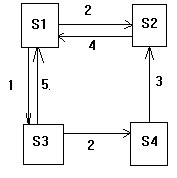
Задача 5. Рассматривается 3-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно 4. Поток заявок, поступающих в СМО, простейший с интенсивностью 8 ед/час. Среднее время обслуживания заявки равно 15 мин. Время обслуживания распределено по показательному закону. Определить вероятность того, что заявка получит отказ в обслуживании.