МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
"Южно-Российский государственный университет экономики и сервиса" (ФГБОУ ВПО «ЮРГУЭС»)
Волгодонский институт сервиса (филиал)
(ВИС ФГБОУ ВПО «ЮРГУЭС»)
Ю.В. Никонорова
Основы теории массового обслуживания
Методические указания
для выполнения контрольных работ
для студентов очной и заочной форм обучения
направлений 100100 «Сервис» бакалавриат
Волгодонск 2011
Составитель:
канд.физ.-мат.наук, доцент кафедры «Экономика и управление»
ФГБОУ ВПО ВИС ЮРГУЭС
Ю.В.Никонорова
Рецензент:
канд. физ.-мат.наук, доцент кафедры «Естественнонаучные и гуманитарные дисциплины» ФГБОУ ВПО ВИС ЮРГУЭС
А.Г. Кремлев
Методические указания разработаны для студентов - бакалавров направлений 100100 «Сервис» ВИС в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования. В методических указаниях изложены задания контрольной работы по десяти вариантам, вопросы к зачету.
Волгодонский институт сервиса (филиал) государственного образовательного учреждения высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса», 2011
Содержание
Введение........................................................................................................ 4
Варианты индивидуальных заданий .......................................................... 4
Вариант №1......................................................................................... 4
Вариант №2......................................................................................... 4
Вариант №3..........................................................................................5
Вариант №4.......................................................................................... 6
Вариант №5.......................................................................................... 7
Вариант №6..........................................................................................7
Вариант №7..........................................................................................8
Вариант №8..........................................................................................9
Вариант №9.........................................................................................10
Вариант №10.......................................................................................10
Вопросы к зачету .........................................................................................11
Библиографический список.........................................................................13
Введение
Одним из требований получения зачета по дисциплине «Основы теории массового обслуживания» является выполнение контрольной работы. Контрольная работа оформляется согласно Стандарту (СТО ЮРГУЭС 01-2009). В контрольной работе необходимо подробно раскрыть указанную тему (задача 1) и решить 4 следующие задачи.
Вариант задания соответствует последней цифре в зачетной книжке.
Варианты индивидуальных заданий Вариант №1
Задача 1. Подробно раскрыть тему: Эффективность функционирования СМО.
Задача 2. В справочное бюро обращается в среднем 2 человека за 10 минут. Найти вероятность того, что за 30 минут за справкой обратится 4 человека.
Задача 3. В билетной кассе работает один кассир, обслуживающий в среднем двух покупателей за одну минуту. Каждый час в среднем приходят покупать билеты 90 посетителей. Провести анализ работы СМО.
Задача 4. Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие.
а) составить матрицу интенсивностей переходов;
б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;
в) найти предельное распределение
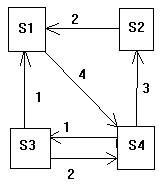
Задача 5. Рассматривается 3-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно 4. Поток заявок, поступающих в СМО, простейший с интенсивностью 6 ед/час. Среднее время обслуживания заявки равно 15 мин. Время обслуживания распределено по показательному закону. Определить относительную пропускную способность.
Вариант №2
Задача 1. Подробно раскрыть тему: Типы моделей СМО. Привести примеры.
Задача 2. В приборе имеются два блока, работающих независимо друг от друга. Время безотказной работы определяется показательным законом. Среднее время безотказной работы 1-го блока 2 года, 2-го –1 год. Найти вероятность того, что за 1,5 года не откажет ни один из блоков.
Задача 3. На склад в среднем прибывает 3 машины в час. Разгрузку осуществляют 3 бригады грузчиков. Среднее время разгрузки машины - 1час. В очереди в ожидании разгрузки могут находиться не более 4-х машин. Дать оценку работы СМО.
Задача 4. Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие.
а) составить матрицу интенсивностей переходов;
б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;
в) найти предельное распределение
Задача 5. Рассматривается 4-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно 3. Поток заявок, поступающих в СМО, простейший с интенсивностью 9 ед/час. Среднее время обслуживания заявки равно 20 мин. Время обслуживания распределено по показательному закону. Определить абсолютную пропускную способность.
Вариант №3
Задача 1. Подробно раскрыть тему: Одноканальная СМО с отказами.
Задача 2. Секретарю директора завода поступает в среднем 1,2 телефонных вызовов в минуту. Средняя продолжительность разговора составляет 2 минуты. Найти основные характеристики СМО и оценить эффективность её работы.
Задача 3. Интенсивность потока посетителей столовой составляет 150 человек в час. Имеется 3 кассира, каждый из которых обслуживает в среднем 1 посетителя за минуту. Найти характеристики СМО.
Задача 4. Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие.
а) составить матрицу интенсивностей переходов;
б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;
в) найти предельное распределение
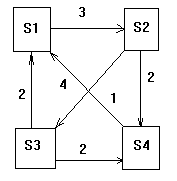
Задача 5. Рассматривается 4-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно 3. Поток заявок, поступающих в СМО, простейший с интенсивностью 5 ед/час. Среднее время обслуживания заявки равно 30 мин. Время обслуживания распределено по показательному закону. Определить вероятность того, что не более 2-х каналов будет занято обслуживанием.