Критерии согласия

При помощи критериев согласия проверяется гипотеза о соответствии эмпирической функции распределения выборки (совокупности числовых результатов натурных измерений) какой-либо аналитической функции (закону распределения). В качестве так называемой нулевой гипотезы принимается предположение о соответствии эмпирической и теоретической (аналитической) функций распределения, а в качестве альтернативной (противоположной) – их несоответствие. Степень согласия оценивается при помощи специально рассчитываемых величин, которые называются статистиками. Естественно, различные критерии (тесты) используют для оценки степени согласия разные статистики. Наиболее часто применяются критерий хи-квадрат Пирсона, критерий Колмогорова и критерий n² (Крамера-Мизеса-Смирнова).

Тестовой статистикой последнего критерия является сумма квадратов разностей между аналитической P(x) и эмпирической P^(x) функциями обеспеченностей по всем значениям случайной величины x:

_n

n² = [P^(x)- P (x)]² +1/(12n)

ⁱ⁼¹

Напомним, что обеспеченность – это величина, обратная интегральной функции распределения F(x). Если последняя показывает вероятность того, что случайная величина не превысит некоторого заданного значения, то функция обеспеченности, наоборот, показывает вероятность того, что случайная величина будет равна заданному значению или превысит его. Разумеется, во всех тестовых статистиках несложно заменить функцию обеспеченности интегральной функцией распределения: P(x) = 1-F(x). Широкое использование именно функции обеспеченности объясняется тем обстоятельством, что очень часто для практических целей необходимо знать вероятность того, что случайная величина примет какое-либо определенное значение или превысит его. Так, при мониторинге состояния окружающей среды очень важно определить вероятность превышения ПДК, при прогнозе опасных явлений – вероятность штормового усиления ветра, увеличения высоты волны в море, выпадения большого количества осадков, которое может вызвать наводнение и т.п.

Обыкновенно мы имеем дело с выборками небольшого объема (проще говоря, число измерений ограничено). Члены выборки ранжируются, т.е. располагаются в убывающем или возрастающем порядке. Допустим, имеется ряд величин какой-либо характеристики, расположенных в убывающем порядке:

x₁>x₂>x₃>…>x_m>…>x_n . Тогда теоретическая вероятность превышения для m-го члена ряда может быть выражена формулой

P{X x_m}=lim(m/N) N

Однако длина реальной выборки конечна, n<. Можно приблизительно оценить вероятность превышения каждого члена имеющейся выборки:

P^*_m =P{X x_m} m/n,

где m – порядковый номер x_m в ранжированном ряду, P^*_m - обеспеченность m-го члена ранжированного ряда. В соответствии с данной формулой обеспеченность первого (самого большого) члена ранжированного ряда будет равна 1/n, второго – 2/n, последнего – n/n=1. Таким образом, последний член ранжированного ряда представляет собой абсолютный минимум и СВ никогда не примет значение меньше x_n. Данный парадокс возникает в связи с тем, что мы заменили N на n. В действительности можно получить бесконечное множество выборок из генеральной совокупности длиной n, каждая из которых будет иметь свой максимум и свой минимум. В этом смысле эмпирическая обеспеченность m-го члена ранжированного ряда сама будет являться случайной величиной, и в качестве расчетного значения разумно принять её математическое ожидание, моду или иную устойчивую характеристику. В настоящее время разработано около десятка формул для расчета эмпирической обеспеченности. Часто применяются следующие три формулы:

А.Хазена P^*_m =(m-0.5)/n

С.Н.Крицкого-М.Ф.Менкеля (Вейбула) P^*_m =m/(n+1)

Н.Н.Чегодаева P^*_m = (m-0.3)/(n+0.4)

Формула Хазена фактически предполагает замену ступенчатого графика эмпирических частот сглаженной кривой, проходящей через середины ступенек графика. Обеспеченность первого члена ряда составит 1/2n. Формула Крицкого-Менкеля соответствует математическому ожиданию эмпирической обеспеченности. Формула Чегодаева - медианному значению эмпирической обеспеченности. Среди перечисленных формул в определенном смысле наилучшей является формула Крицкого-Менкеля, т.к. получаемая по ней оценка эмпирической обеспеченности является состоятельной, несмещенной и эффективной. Несмещенными называются оценки, математическое ожидание которых равно оцениваемому параметру. Оценка называется состоятельной, если она сходится по вероятности к оцениваемому параметру при неограниченном возрастании числа опытов. Оценки, обладающие свойством несмещенности и состоятельности при ограниченном числе опытов могут иметь разные дисперсии. Очевидно, что чем меньше дисперсия оценки, тем меньше вероятность грубой погрешности при определении приближенного значения параметра. Оценка, обладающая минимальной дисперсией, называется эффективной.

При выводе формулы эмпирической обеспеченности допустимо рассуждать и по-иному. Значение СВ, расположенное в ранжированном ряду длиной n на m-м месте тоже является СВ, и можно рассчитать обеспеченность, соответствующую математическому ожиданию или моде m-го члена. Но в такой постановке задача разрешима лишь в том случае, когда закон распределения исходной СВ X известен. Так, для распределения Гумбеля и для экспоненциального распределения: P^*_m=(m-0.44)/(n+0.12); для нормального распределения: P^*_m=(m-3/8)/(n+1/4). Различие этих двух подходов состоит в том, что в первом случае в качестве СВ мы рассматриваем обеспеченность m-го члена ранжированного ряда, а во втором в качестве СВ рассматривается значение m-го члена затем вычисляется обеспеченность его МО или моды.

При использовании критериев согласия необходимо задавать уровень значимости.

Вспомним, что статистической гипотезой является некоторое предположение относительно свойств генеральной совокупности, из которой извлечена выборка. Например, мы взяли в водном объекте 20 проб для определения содержания в воде растворенного кислорода. Эти 20 проб и составляют выборку из генеральной совокупности. Для определения растворенного кислорода по классическому иодометрическому методу Винклера требуется около 200 – 300 мл воды. Таким образом, в составе выборки мы вычерпали из нашего водного объекта 250мл х 20 проб = 5 л. Генеральная совокупность в данном случае – это весь водный объект, вычерпанный на пробы. Для примера возьмём крайне небольшой объект – круглый пруд диаметром 50 м и средней глубиной 1м – что-то вроде Карпиева пруда в Летнем саду. Но его объём составляет около 1963.5 м³, т.е. около 7 853 000 объёмов проб на содержание растворённого кислорода. Следовательно, генеральная совокупность значений данного параметра даже для такого малюсенького объекта неимоверно выше реальной выборки. А ведь экологам приходится делать выводы о состоянии неизмеримо больших водных объектов (Невской губы или Ладожского озера) на основании выборок, которые в лучшем случае имеют десяток-другой значений. Это научно обосновано, если выборка репрезентативна, т.е. отражает свойства объекта в целом. Для этого требуется, чтобы точки отбора проб были равномерно распределены по пространству исследуемого объекта. При обработке выборки мы сначала выдвигаем статистическую гипотезу – в первую очередь гипотезу о достаточной близости распределения значений в выборке нормальному закону. Как раз для проверки гипотез используются специальные тесты, называемые критериями. Критерий (тест) статистической гипотезы – это правило, позволяющее принять или отвергнуть данную гипотезу. Для реализации теста используются определенные функции результатов, называемые статистиками.

Для конкретной выборки (реализации) рассчитывают эмпирическое значение статистики. Очевидно, что величина статистики также является случайной величиной, подчиняющейся какому-то закону распределения, и для различных выборок данной длины значение оценки статистики будет различным. Область возможных значений статистики делится на две части: область принятия гипотезы и критическую область. Если оценка статистики (значение статистики, рассчитанное для данной выборки) попадает в область принятия гипотезы, то эта гипотеза не опровергается, если в критическую область, то гипотеза опровергается. Область принятия гипотезы называется доверительной областью (доверительным интервалом). Законы распределения применяемых статистик являются одномодальными. На рис. 2 представлена функция распределения некоей статистики t.

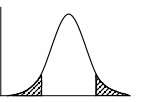f(t)

t

Рис. 2. Доверительная и критические области.

Вероятность по произвольной выборке получить такую оценку статистики, которая попадает в доверительную область, геометрически равна незаштрихованной площади на графике распределения плотности вероятности статистики. Эта вероятность называется доверительной вероятностью p_д. Вероятность попадания оценки статистики в критическую область выражается равенством =1 - p_д. Вероятность  называют уровнем значимости. Если критическая область состоит из двух частей, то вместо  пишут 2 = 1- p_д, где 2 указывает на то, что уровень значимости двусторонний. Геометрически уровень значимости равен заштрихованной площади. Однако уровень значимости, к сожалению, невозможно рассчитать на основании каких-либо внешних параметров. Его приходится принимать, разумеется, не «с потолка», а на основании некоторых соображений. Поэтому здесь кроется некоторая неопределенность, объективно присущая любому исследованию окружающей среды.

Значимости уровень статистического критерия - это вероятность ошибочно отвергнуть основную проверяемую гипотезу (так называемую нулевую гипотезу), когда она верна. В результате проверки статистической гипотезы H могут возникнуть четыре ситуации: гипотеза H на самом деле истинна и принимается согласно критерию; гипотеза, противоположная гипотезе H на самом деле истинна и принимается согласно критерию; гипотеза H на самом деле истинна, но отвергается согласно критерию (ошибка первого рода); гипотеза, противоположная гипотезе H на самом деле истинна, но отвергается согласно критерию (ошибка второго рода).

В первых двух случаях мы получаем правильные заключения, а в двух последних - ошибочные заключения. При проверке гипотез возможны погрешности двух родов. Погрешность первого рода состоит в том, что нулевая гипотеза отвергается в то время, когда она в действительности верна. Чем меньше уровень значимости, тем меньше вероятность отвергнуть верную гипотезу. Погрешность второго рода состоит в том, что нулевая гипотеза принимается, а на самом деле она неверна. Вероятность ошибки первого рода называется уровнем значимости данного критерия. Обычно уровень значимости принимают равным 0.1, 0.05, 0.01, 0.001. Для дискретных случайных величин заданный уровень значимости указывает верхнюю границу для вероятности ошибки первого рода.

Поскольку мы всегда обрабатываем не генеральную совокупность, а реализованную выборку из неё (реализацию), то при проверке какой-либо статистической гипотезы встает вопрос о том, существенно ли различие значения рассчитанной по данной выборке статистики от теоретического значения, соответствующего проверяемой нулевой гипотезе. Причиной этого различия может быть и случайное колебание значений в выборке, а может и ложность нулевой гипотезы. Если сравниваемые значения статистики, т.е. теоретического в соответствии с принятой нулевой гипотезой и полученного по конкретной выборке отличаются друг от друга более, чем это можно разумно приписать случайной вариации значений элементов выборки, то разность между ними называется значимой или существенной. В противном случае разность называется несущественной или случайной.

Весь вопрос в том, как определить границу между существенной и несущественной разницей значений статистики? Для этого сначала необходимо определить уровень значимости, ибо при его различных значениях различным будет положение границы между случайной и значимой разницей значений статистики. Граница между вероятностью существенного и несущественного различия называется уровнем значимости и часто обозначается через . Если вероятность полученной статистики равна или меньше уровня значимости, то гипотеза опровергается. Можно дать другое определение: уровень значимости — это вероятность события, которой решено пренебречь.

Значения статистики, при которых гипотеза опровергается, т.е. вероятность которых меньше заданного уровня значимости , образуют критическую область проверяемой гипотезы. Значения статистики, при которых гипотеза не опровергается, образуют доверительную область. Границы между критической и доверительной областью называются доверительными границами. Задача проверки гипотезы сводится к построению критической области рассматриваемой статистики для данного уровня значимости. Если статистика попадает в критическую область, то этот факт указывает на несоответствие гипотезы наблюденным данным, и гипотеза опровергается.

При помощи критерия значимости нулевая гипотеза может быть опровергнута. Но даже если гипотеза не опровергнута, это еще не значит, что она верна. На это необходимо обратить особое внимание. Только в случае достаточно высокой вероятности полученного результата при данной нулевой гипотезе можно утверждать, что рассматриваемая гипотеза, по-видимому, верна.

Выбор уровня значимости или вероятности события, которой решено пренебречь в данной области исследования, производится до некоторой степени произвольно. Он устанавливается на основании опыта, как уровень, дающий определенную практическую уверенность, что ошибочные заключения будут сделаны только в очень редких случаях. Например, в гидрометеорологических расчетах и прогнозах широкое употребление имеют 10, 5, а нередко используется и 1 %-й уровень значимости (=10, 5, 1 %). В других областях научных исследований уровень значимости может быть другим.

Для понимания смысла уровня значимости рассмотрим ряд «житейских» примеров. Предположим, мы хотим приобрести ящик яблок, для ровного счета 100 штук. На вопрос о качестве товара продавец говорит нам, что яблоки отличные, ну может быть, от силы одно – два немного подгнили. Мы согласны с такое долей некондиции и для проверки вынимаем из ящика первое попавшееся под руку яблоко – оно оказывается гнилым. Берем второе – тоже гниль. Скорее всего, мы прекратим испытания и не станем покупать этот товар. То есть мы пренебрегли вероятностью того, что мы вытащили из ящика два единственные гнилые яблока, а остальные – высшего сорта. Посмотрим, какова вероятность этого события? Вероятность вытащить в первом испытании гнилое яблоко – 2/100, во втором – 1/99. Соответственно вероятность вытащить в первом и втором случаях гнилые яблоки - 2/100*1/99 = 0.0002. Т.е. мы интуитивно пренебрегаем возможностью столь маловероятного события, хотя оно в принципе возможно. Другой случай: разработка и установка системы аварийного отключения какого-либо потенциально опасного промышленного объекта (атомного или химического реактора и т.п.). Разработчик утверждает, что вероятность отказа – 1 случай на миллион, однако при проверке система не срабатывает. Вероятно, приемная комиссия не поверит, что она столкнулась именно с этим случаем, а в остальных 999999 случаях система будет работать великолепно. Третий пример из сессионной студенческой жизни: имеется 20 экзаменационных билетов по два вопроса в каждом, причем вопросы скомпонованы в билеты случайным образом. Студент отлично отвечает на оба вопроса и получает соответствующую оценку без дополнительных вопросов. Это означает, что экзаменатор пренебрегает вероятностью того, что студент знает ответы только на эти два вопроса, а остальной курс ему незнаком. Посмотрим, какова эта вероятность: 2/40*1/39 = 0.0013 или уровень значимости 0.128%. А если студент знает только половину курса? В этом случае уровень значимости будет дольно велик: 20/40*19/39 = 24.4%. То есть экзаменатор при правильном ответе студента на оба вопроса билета с очень большой долей вероятности может быть уверен в том, что экзаменуемый студент знает ещё что-то, но для уверенности в том, что студент знает больше половины курса необходимо задать дополнительные вопросы.

При увеличении уровня значимости увеличивается критическая область, а следовательно, возрастает и вероятность попадания исследуемой статистики в критическую область. Таким образом, возрастает и вероятность ошибочного отбрасывания выдвинутой гипотезы. Например, при уровне значимости , равном 20 %, будут опровергаться все гипотезы, вероятность статистик которых составляет 20 % и менее. Однако попадание значения статистики в критическую область в случае правильности нулевой гипотезы возможно в среднем в одном из пяти случаев. Поэтому к отбрасыванию гипотез при больших уровнях значимости надо подходить очень осторожно.

Казалось бы, в чем же тогда дело? Давайте назначать уровень значимости как можно меньше. Однако с уменьшением уровня значимости возрастает число испытаний (в нашем случае – проб, измерений), необходимых для эффективного применения критерия значимости, так как при малом объеме выборок возможна такая ситуация, когда применение данного теста (статистики) вообще не корректно. В качестве основного критерия при выборе уровня значимости выступает только возможность его использования на практике. С одной стороны, этот уровень должен быть достаточно велик для отбрасывания ложных гипотез, а с другой — он должен быть достаточно мал, чтобы приводить к отбрасыванию лишь немногих верных гипотез. Поэтому в каждой области исследований обычно применяется несколько уровней значимости и в каждом конкретном случае выбирают тот уровень, который оптимален задаче данного исследования. При этом необходимо учитывать следующие важные обстоятельства:

1. Уровень значимости уменьшается с повышением важности расчета. Так, если проверяются, например, гипотезы о надежности или возможности отказа какого-то важного технического устройства или конструкции, то уровень значимости может быть принят равным даже 0,1 %.

2. Уровень значимости должен быть в какой-то степени согласован с точностью исследуемых исходных данных и возможностью увеличения объема выборки. Если, например, точность измерений не превышает 5 %, то использование уровня значимости меньше 5 % не всегда достаточно обосновано.

В качестве уровня значимости принимается такое достаточно малое значение вероят­ности, которое характеризует практически невероятное (маловероятное) событие для данной сферы практической деятельности или научного исследования. Назначение уровня значимости не является математической задачей. Уровень значимости устанавли­вается исходя из тех последствий, которые возможны вследствие совершения ошибки при принятии или отклонении данной гипотезы. Уровень значимости (в литературе встреча­ется обозначение p-уровень) – это показатель, находящийся в обратной зависимости от надёжности результата. Более высокий уровень значимости соответствует более низкому уровню доверия к результату проверки статистической гипотезы.

Как определить, является ли результат действительно значимым? Не существует никакого способа избежать произвола при принятии решения о том, какой уровень значимости следует действительно считать "значимым". Выбор определенного уровня значимости, выше которого результаты отвергаются как ложные, довольно произволен. На практике окончательное решение обычно зависит от того, был ли результат предсказан априори (т.е. до проведения натурных исследований) или обнаружен апостериорно в результате многих анализов и сравнений, выполненных с множеством данных, а также на традиции, имеющейся в данной области исследований. Обычно во многих областях знания уровень значимости в 5% является приемлемой границей статистической значимости, однако следует помнить, что этот уровень все ещё включает довольно большую вероятность ошибки (5%). Результаты, значимые на уровне 1% обычно рассматриваются как статистически значимые, а результаты с уровнем 0.5% или 0.1% как высоко значимые. Однако следует понимать, что данная классификация уровней значимости является всего лишь неформальным соглашением, принятым на основе практического опыта.

При проверке статистических гипотез необходимо различать двухсторонний и односторонний уровень значимости. Так, если при сравнении двух случайных величин требуется оценить их разницу, т. е. одинаковый интерес представляют как положительная, так и отрицательная разность между изучаемыми величинами, то при 5 %-м уровне значимости, берется по 2,5 % на каждом «конце» функции распределения данной статистики. Наиболее часто эта ситуация встречается при проверке средних значе­ний, когда одинаково важны существенные отклонения как в положительную, так и в отрицательную сто­рону. Односторонний критерий значимости используется в тех случаях, когда надо убедиться, что одно зна­чение строго больше (меньше) другого, например: концентрация загрязняющего вещества в одном объекте значимо выше его содержания в другом.

При проверке гипотезы определяется вероятность того, что полученное отклонение оценки статистической характеристики от ее теоретического, соответствующего выдвинутой гипотезе значения больше или меньше допустимого при данном уровне значимости. Область принятия гипотезы называется доверительной областью (доверительным интервалом). Вероятность по произвольной выборке получить статистику, которая попадает в доверительную область называется доверительной вероятностью (р_д). Вероятность попадания оценки статистики в критическую область выражается равенством  = 1 - р_д. Если критическая область состоит из двух частей (два «конца» функции распределения вероятности данной статистики), то вместо  используют обозначение 2 = 1 - р_д, где 2 указывает на то, что уровень значимости двусторонний. Геометрически уровень значимости равен заштрихованной площади на рис. 2.

Необходимо подчеркнуть, что при проверке статистических гипотез следует избегать категорических формулировок типа: «гипотеза верна» или «гипотеза неверна». Если значение анализируемой статистики не попадает в критическую область, говорят: нулевая гипотеза H₀ не опровергается при принятом уровне значимости ; если попадает, говорят: H₀ опровергается при уровне значимости , т.е. расхождение эмпирических данных с нулевой гипотезой статистически значимо.

Возможен другой подход при оценке статистических гипотез. Он заключается в том, что при анализе какой-либо статистики границы доверительной области не фиксируются путем назначения уровня значимости. Вместо этого решается обратная задача: определяется максимальный уровень значимости, при котором статистика ещё попадает в доверительную область, т.е. нулевая гипотеза не опровергается. В этом случае говорят: гипотеза не опровергается при таком-то уровне значимости, результат интерпретируется в соответствии с приведенной ниже таблицей.

Табл. 1.

Традиционная интерпретация максимальных уровней значимости

	Значимость соответствия эмпирических данных и H0
>0.1	Гипотеза H0 почти наверняка не опровергается
0.05	Довольно сильный довод в пользу H0
0.02	Некоторые сомнения в истинности H0
0.01	Сильные сомнения в истинности H0

Как уже упоминалось (с. 27), тестовая статистика nω² определяется суммой квадратов разниц между теоретической (предполагаемой) и реальной функциями обеспеченностей. При n>40 распределение статистики nω² не зависит от вида исходного теоретического распределения и близко к некоторому предельному распределению. Благодаря применению этого критерия наиболее полно используется вся первичная информация.