Построение гистограммы частотного распределения

Импорт данных в вектор v:

v

Определение числа членов выборки m:

Определение оценки математического ожидания (sred) и среднего квадратичного отклонения (sko):

Определение числа градаций n: принимается, что оно равно частному от деления количества членов выборки на 5. В результате отбрасывается дробная часть. Если получается, что число градаций меньше 5, то за число градаций берётся 5. Максимальное число градаций – 21.

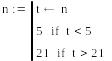
Затем определяем минимальное, максимальное значения в выборке и её размах.

Далее определяем порядок размаха и шкалу градаций. В представленном ниже цикле последовательно увеличиваем значение максимального значения выборки в 10 раз, пока это значение не станет больше 1 и, таким образом, выясняем порядок максимального значения.

Определяем «условно увеличенное максимальное значение»:

Получаем ближайшее к нему целое «сверху»:

Определяем разницу между увеличенной границей и увеличенным максимальным значением:

Если разница больше половины порядка, то снижаем значение верхней границы на половину порядка.

_{Определяем реальное значение верхней границы.}

Аналогичные действия выполняем для определения значения нижней границы по оси X.

В качестве верхней и нижней границ значений по оси X берутся ближайшие к максимальному и минимальному значениям выборки кратные половине порядка значения. Естественно, нижняя граница меньше минимального значения, а верхняя больше. Так, для нашего примера:

Далее создаётся порядковая индексная переменная (индексы градаций) j:

Затем рассчитывается шаг градации h:

_{После этого создаём одномерный массив (вектор) значений границ градаций int:}

При помощи функции histogram строим матрицу (двумерный массив) f, первая колонка которой содержит значения середин градаций, а вторая – количество «попавших» в эту градацию значений выборки.

Далее создаем матрицу gist, первый столбец которой совпадает с первым столбцом матрицы f и содержит значения середин градаций, а второй содержит соответствующие частоты. Обратите внимание, что первый столбец матрицы имеет номер 0.

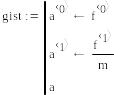
Строим функцию нормального закона плотности вероятности:

Затем непосредственно строится гистограмма и линия нормаль­ного распределения:

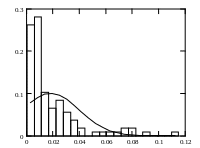
Рис. 1. Пример построения гистограммы распределения в пакете Mathcad.

Для создания графика в пакете Mathcad следует на панели интерфейса нажать «Вставка», а в появившемся ниспадающем меню – «График», затем – «Точка X-Y». В рабочей области появятся внешняя и внутренняя рамки поля графика. По оси X поставить идентификатор первого столбца матрицы, полученной при помощи функции histogram, а по оси Y – второго. В нашем примере это, соответственно, _{и .Для добавления кривой нормального распределения за последним обозначением следует поставить символ «,» и F( ), а затем – «Ввод».}

Закономерен вопрос: «Как быть, если применение экспресс-метода и построение гистограммы частотного распределения не разрешили наши сомнения в том, принадлежит или не принадлежит данная выборка нормальному закону распределения?» В этом случае необходимо выяснить, существенно или несущественно различие между распределением совокупности данных наблюдений и теоретическим нормальным распределением при помощи критериев согласия.