Линейная интерполяция

Необходимы два вектора значений в узлах: аргумента и функции. Для примера возьмем временную интерполяцию значений температуры воды в каком-либо водоёме. Здесь значениями аргумента будут номера суток от начала года, в которые производились измерения температуры, а значениями функции – сами величины температуры воды. В принципе можно импортировать в рабочую область пакета Mathcad эти два вектора из отдельных файлов. Однако каждому значению аргумента должно соответствовать конкретное значение функции. Чтобы «застраховать» себя от ошибок, значения аргумента и функции лучше «держать» в двух колонках одной таблицы, которая импортируется в виде матрицы. Первая колонка (номер 0) содержит номера суток, вторая (номер 1) - значения температуры.

data

При этом значения аргумента должны идти в порядке возрастания, т.е. матрицу следует отсортировать по возрастанию значений первой колонки.

Функция linterp(X,Y,t) Маткада выполняет линейную интерполяцию. Здесь X – вектор значений аргумента в узлах, Y – вектор значений интерполируемой функции в узлах, t – значение или группа значений (вектор) аргумента, для которого (-ых) необходимо получить значения функции. При этом значение t должно лежать в пределах изменения элементов вектора vx.

fit(x):=linterp(X,Y,t)

_{Размерность переменной fit(t) определяется тем, является ли x отдельным значением или вектором. В вектор alldata импортируется 365 значений годового хода температуры воды. На рис. 4 приводится сравнение результата линейной интерполяции с годовым ходом температуры воды.}

Сплайновые интерполяции

_{Разумеется, желательно соединять узлы (точки) не ломаной линией, а гладкой кривой. Для этого может применяться интерполяция кубическими сплайнами, т.е. отрезками кубических парабол.}

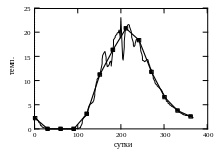_{Рис. 4. Годовой ход температуры воды и её линейная интерполяция (жирная линия) по 13 значениям (интервал 30 суток).}

В программном пакете Mathcad аппроксимацию кубическими сплайнами производит функция interp(S,X,Y,t). Сплайн-интерполяция сложнее линейной: перед применением функции interp необходимо определить первый из её аргументов – вектор вторых производных S. Сплайн-интерполяция состоит в аппроксимации промежутков между точками функциями вида f(t)=at³+bt²+ct+d. Коэффициенты a, b, c, d рассчитываются отдельно для каждого промежутка в зависимости от значений y_i в соседних точках. Значения вектора S должны быть рассчитаны при помощи одной из функций: lspline(X,Y), pspline(X,Y), cspline(X,Y). Эти функции возвращают соответственно векторы значений коэффициентов линейного, квадратичного и кубического сплайнов. Выбор вида функции расчета сплайновых коэффициентов влияет на интерполяцию вблизи конечных узлов области X. Так, в первом случае сплайн на границе области преобразуется в линейную функцию. Во втором - в параболу, а в третьем результирующая функция также является кубическим сплайном. Особенно сильно проявляются различия в результатах экстраполяции за пределами области X. Как видно на рис. 5, в пределах области значений X нет существенной разницы в результатах интерполяции, она заметна лишь за краями области X. Сходство кубической сплайн-интерполяции с линейной состоит в том, что в обоих случаях соединение результирующих функций происходит в узлах.

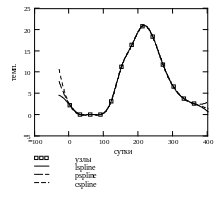
Рис. 5. Кубическая сплайн-интерполяция с применением различных функций для расчёта вектора вторых производных S.

Еще более сложной является интерполяция В-сплайнами. Здесь соединение сплайнов происходит не в точках исходных интерполируемых значений, а совершенно в других точках, значения аргументов которых предлагается пользователю задать в векторе U. Сплайны могут быть полиномами 1, 2 или 3 степени (линейные, квадратичные или кубические). Интерполяция также выполняется при помощи функции

interp(S,X,Y,t). Различие состоит в том, что вектор S рассчитывается функцией bspline (X,Y,U,n), которая возвращает вектор значений коэффициентов В-сплайна (вторых производных). Здесь n – порядок полиномов сплайновой интерполяции (1, 2, 3). Размерность вектора U должна быть на 1, 2 или 3 меньше размерности векторов X и Y. Первый элемент вектора U должен быть меньше первого элемента вектора X, а последний элемент U – больше последнего элемента вектора X.

Рис. 6. Полиномиальная сплайн-интерполяция