Лабораторная работа 2. Измерение скорости пули методом баллистического маятника.

Оборудование: баллистический маятник, пуля, пистолет и шкала.

Цель работы: применение законов сохранения импульса к решению конкретной задачи. Упругий и неупругий удар.

1.Теоретическое введение

Измерение скорости пули основано на теории центральных ударов тел, изложенной в литературе.

Б аллистический маятник - это тяжелое тело массой М, подвешенное на длинной нити ℓ. Пуля массой m, летящая горизонтально со скоростью , попадает в центр маятника и застревает в нем (абсолютно неупругий удар). После удара система тел (М+m) получает скорость и отклоняется от положения равновесия на расстояние d. Силами сопротивления воздуха можно пренебречь. Силами трения нити в местах подвески также можно пренебречь. Поэтому систему "пуля-маятник" считают изолированной. Запишем для нее закон сохранения импульса:

(1).

Скорость системы тел υ₁ определяется из условия, что после удара кинетическая энергия системы (М+m) переходит в потенциальную энергию на высоте h. Запишем закон сохранения энергии для данного случая:

. (2).

Из рис. 1 следует, что величина h, входящая в уравнение (2), выражается через угол  и длину отклонения d₁ ≈ d.

h = ℓ - ℓcos = ℓ(1 - cos) = 2ℓ sin²(/2), (3)

но sin  d₁ /ℓ , поэтому sin(/2) = d₁/2ℓ. (4)

Решим совместно уравнения 1, 2, 3, 4 - получим выражение для  скорости пули:

(5)

2.Описание лабораторной установки и метода измерения

Установка (баллистический маятник), изображенная на рисунке 2 – это массивная металлическая шайба 1 подвешенная на упругих нитях 2. На шайбе расположен указатель 3, который направлен на сантиметровую линейку 4. Пуля 5 выстреливается при помощи баллистического пистолета 6, который направлен в центр шайбы. Для того чтобы удар был неупругий (т.е. при ударе пуля застревает в шайбе), на одну из поверхностей нанесен пластилин 7. Для того чтобы пистолет произвел выстрел, его надо зарядить. Для зарядки пистолета необходимо оттянуть курок 8 и развернуть по оси (рис. 2). После зарядки в пистолет вставляется пуля 5 и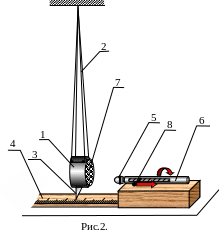 поворотом курка в обратную сторону производится выстрел. Максимальное отклонение маятника d фиксируется на сантиметровой шкале 4 при помощи указателя 3.

3.Порядок выполнения работы

1. Расположите незаряженный пружинный пистолет вблизи маятника так, чтобы быть уверенным, что пуля попадет в центр маятника. Затем зарядите.

2. Произведите 3 выстрела и для каждого из них определите смещение d по шкале и запишите в таблицу 1.

3. Произведите тот же опыт еще с двумя пулями.

4. Все результаты опытов занесите в таблицу 1.

4. Обработка результатов измерения

1. Подсчитайте средние значения смещения маятника для каждой из пуль.

2. По средним значениям смещений d_ср, пользуясь формулой (5), рассчитайте значение скорости пули 

3. Подсчитайте погрешность по формуле: ,

где ΔM = Δm = 0,0005 кг – погрешность весов;

- средняя ошибка смещения d для каждой пули;

Δl = 0,005 м инструментальная погрешность измерительной линейки;

Δg = 0,007 м/с² выбирается такая величина, если при расчетах величину ускорения свободного падения g считать равной 9,8 м/с². Отсюда: Δg=9,807 -9,8 = 0,007 м/с².

4. Занесите все результаты измерений и вычислений в таблицу 1. Для каждой из пуль запишите значение скорости в виде: υ = υ_ср ± Δυ. Результаты сравнить.

5. Сделайте вывод по работе.

Таблица 1.

m, кг	№	d, м	dcp, м	Δd, м	Δdcp, м	υср, м/c	Δυ, м/c
m1=	1							M = 1,248 кг ; ℓ = 1,84 м
	2
	3
υ = υср ± Δυ υ =
m2=	1
	2
	3
υ = υср ± Δυ υ =
m3=	1
	2
	3
υ = υср ± Δυ υ =

Выводы:__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ВОПРОСЫ:

1. Что называется массой? Скоростью? Импульсом? Энергией?

2. Законы сохранения импульса и энергии.

3. Применение законов сохранения импульса и энергии для расчета скорости пули методом баллистического маятника при их неупругом соударении.

4. Применение законов сохранения импульсов и энергии при изучении упругого соударения тел.

Для расчетов

дата выполнения_____________________________

Преподаватель_____________________________