Пример задания на выполнение курсового проекта

КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Автоматизации производственных процессов

^{(наименование кафедры)}

Утверждаю:

Зв. кафедрой

К.т.н., доцент ______________________Петриченко Г.С.

ЗАДАНИЕ

на курсовое проектирование

Магистранту: __09-КБ-ИВ-01________ группы __________3________курса

факультета ________________КТАС_____________________________

направления подготовки 220201 – «Управление и информатика в технических системах» Иванову Н.Н.

Тема проекта: Расчет оптимального управления методом множителей Лагранжа.

Содержание задания: Разработка оптимального управления методом множителей Лагранжа

Объем работы:

а) пояснительная записка к проекту ______20________ листов формата A4

Рекомендуемая литература: список литературы

______________________________________________________________

Срок выполнения проекта: с “___”________ по “ ” 2013 г.

Срок защиты: “___” _______2013_г.

Дата выдачи задания: “___” февраля 2013_г.

Дата сдачи проекта на кафедру: “___”_________2013 г.

Руководитель проекта ___________доцент Горохов Д.А.

^{(подпись, ф.и.о., звание, степень)}

Задание принял студент _______________________________._________

^{(подпись, дата)}

Приложение 3

Пример выполнения и оформления курсовой работы на тему " Расчет оптимального управления методом множителей Лагранжа при различных граничных условиях"

Реферат

Пояснительная записка курсовой работы содержит 21 страницу, 17 рисунков и 0 таблиц.

Ключевые слова: оптимальное управление, оптимальная система управления, объект управления, граничные условия, функционал, задача с закрепленными концами.

Использование оптимальных систем управления предполагает расчет оптимального управления и соответствующих фазовых координат.

Введение

При отсутствии возмущений, действующих на объект управления, возникает необходимость использования оптимальной системы управления.

В данном случае среди оптимальных систем управления может быть выбрана система, состоящая из программатора и объекта управления. Ее расчет предполагает определение оптимального управления методом множителей Лагранжа. Методика расчета определяется типом граничных условий.

1. Постановка задачи

Задана оптимальная система управления, структурная схема которой имеет вид (рис. 1).

Рис. 1. Оптимальная система управления

Разработать оптимальное управление и соответствующие ему фазовые координаты для различных граничных условий.

1. Расчет оптимального управления методом множителей Лагранжа в задаче с закрепленными концами и фиксированным временем.

В системе автоматического управления в качестве объекта управления рассматривается двигатель постоянного тока.

Дифференциальное уравнение, описывающее вращение его вала, можно представить в виде:

(1)

где I – момент инерции вращающейся части двигателя;

φ – угол поворота вала двигателя;

i_я – ток в якорной цепи;

k_ф – конструктивная постоянная;

Ф — магнитный поток;

М_с – момент сопротивления.

Используя обозначения

, , , ,

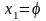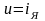уравнение (1) можно записать в нормальной форме:

, . (2)

Найдем оптимальное управление валом двигателя, при котором вал повернется на угол 1 рад за 1 с и остановится. Поворот вала происходит при минимальном расходе энергии с моментом сопротивления равным:

С учетом принятых обозначений это выражение принимает вид:

(3)

Пусть коэффициенты в выражениях (2) и (3) равны:

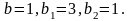
Задача определения оптимального управления математически формулируется следующим образом:

• Модель системы автоматического управления:

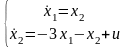(4)

• Граничные условия:

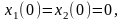
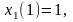
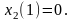(5)

• Функционал:

(6)

Решение.

Запишем гамильтониан с учетом ψ₀ = –1:

(7)

Необходимыми условиями экстремума (уравнения Эйлера-Лагранжа) принимают вид:

(8)

(9)

. (10)

Из уравнения (10) получим:

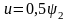(11)

Подставим равенство (11) во второе уравнение системы (4). Объединив систему уравнений (4) и уравнения (8),(9), получим систему дифференциальных уравнений:

(12)

Эту систему линейных однородных дифференциальных уравнений необходимо решить. Систему (12) представим в матричном виде:

(13)

где , а матрица А в данном случае имеет вид:

(14)

Решение будем искать в экспоненциальном виде:

(15)

где _j (j = 1…4)  собственные числа (корни характеристического уравнения) матрицы А (определенные выше);

 собственные векторы, соответствующие числам _j;

С_j  постоянные, определяемые через дополнительные условия.

Определим собственные числа и собственные векторы с помощью программы Mathcad. Для этого введем матрицу А. Это можно сделать, вызвав палитру математических знаков:

Записав А:= , вызываем шаблон матрицы нажатием в палитре Матрица на символ . При этом появится окно установки размеров (параметров) матрицы:

Далее вводим элементы матрицы и получаем:

На панели инструментов щелкаем по символу ввода функций и выводим матричную функцию eigenvals (М), которая возвращает вектор, содержащий собственные значения матрицы:

При этом в шаблон функции надо вставить имя матрицы, т.е. А. Далее, выйдя курсором за правую скобку функции, нажимаем на клавиатуре на клавишу = и получаем искомый вектор собственных значений матрицы в виде:

Следовательно, λ₁ = – 0,5 + i ·1,658; λ₂ = – 0,5 – i ·1,658; λ₃ = 0,5 + i ·1,658; λ₄ = 0,5 – i ·1,658. Далее находим собственные векторы найденных корней. Для этого вводим аналогичным образом функцию eigenvесs (М), возвращающую матрицу, столбцами которой являются собственные векторы корней (порядок расположения собственных векторов соответствует порядку собственных значений, возвращаемых функцией eigenvals):

Следовательно, можно записать:

;

;

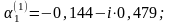
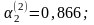
Для нахождения постоянных С₁…C₄ воспользуемся граничными условиями (5). Из первых двух уравнений системы (15) получаем:

(16)

или в матричной форме:

MC = N, (17)

где

, (18)

N = [0, 0, 1, 0]^Т. (19)

С = [C₁, C₂, C₃, C₄­]^T  вектор, подлежащий определению.

Решение будем искать в матричном виде С = М^{– 1}N с помощью программы Mathcad. Для этого введем матрицы М и N:

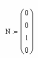
Далее введем выражение С = М^{– 1}N→ и получаем:

Следует иметь ввиду, что матрица М^{– 1} вводится написанием символа М и последующим щелчком по символу 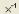в палитре Матрица. Следовательно, можно записать:

С₁ = – 1, 512 – i·1,311; С₂ = – 1, 512 + i·1,311; С₃ = 5,774 – i·9,338;

С₄ = 5,774 + i·9,338.

Перепишем систему (15) следующим образом::

(20)

где (21)

Найдем коэффициенты . Для этого перемножим матрицы:

где и

Выполним эту операцию в программе Mathcad и получим:

Следовательно, получены следующая матрица коэффициентов :

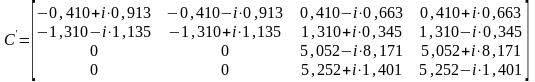
Далее получим решение в обыкновенном виде, перейдя от комплексных функций к действительным. Для этого рассмотрим, например, первые два слагаемых первого уравнения системы (20). Показатели степени экспонент ₁ и ₂  комплексно сопряженные числа. Примем , тогда

(22)

Применим известные равенства

, (23)

. (24)

Подставляя (23), (24) в (22), после преобразований получим:

(25)

Решение не должно содержать мнимой части, поэтому очевидно:

, (26)

что подтверждается предыдущим расчетом.

С учетом (26) окончательно запишем

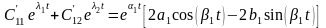. (27)

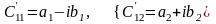Если или , то выражение (27) принимает вид:

(28)

Если , то выражение (27) принимает вид:

(29)

Если или , то выражение (27) принимает вид:

(30)

Аналогично поступая со всеми слагаемыми решения, содержащими экспоненты комплексно сопряженных чисел, решение системы уравнений представим в виде:

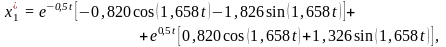(31)

(32)

, (33)

. (34)

Полученные результаты позволяют найти оптимальное управление:

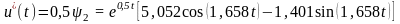(35)

Равенства (31),(32) и (35) представляют собой оптимальные фазовые координаты и оптимальное управление. Построим графики этих функций в программе Mathcad. Введем на рабочем поле функцию оптимального управления:

Введем шаблон графика функции одной переменной. Для этого в палитре Математика щелкнем по символу , появится палитра Диаграмма:

В ней щелкнем по символу , появится требуемый шаблон:

Введем по вертикальной оси функцию u(t), а по горизонтальной t. Щелкнем за пределами области построения графика левой кнопкой и появится исковый график:

Растягиванием увеличим область графика и введем масштабную сетку. Щелкнем два раза по области графика, появится контекстное меню:

В нем по осям Х и У установим флажки в окнах Линии Сетки. В результате получим:

Однако он нас не может удовлетворит этот график, т.к. нам интересен интервал изменения времени от 0 до 1с. Построим требуемую нам область графика. Для этого щелкнем правой кнопкой мыши по графику, появится контекстное меню.:

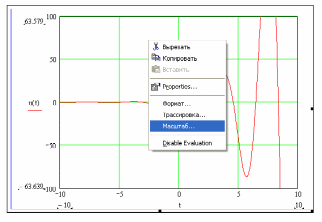
В нем щелкнем по строке «масштаб», появится контекстное меню:

Выделим приблизительно требуемую область графика:

Щелкнув ОК, получим:

Повторим эту операцию до тех пор, пока не получим требуемый график:

Построим аналогичным образом с помощью программы Mathcad графики фазовых координат:

Значение функционала определим интегрированием с помощью программы Mathcad. Для этого в палитре математике щелкнем по символу . Появится палитра Вычисления:

В ней щелкнем по символу определенного интеграла , чтобы появился шаблон:

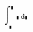
Введем в него необходимые данные и получим результат:

Следовательно, J = 11,551.

Соберем в программе VisSim рассматриваемую модель системы оптимального управления, содержащую программатор, реализующий найденное оптимальное управление:

В качестве программатора используется блок задания выражения expression. Его можно взять в меню Bloсks:

В него вводится выражение для полученного оптимального управления, используя в качестве переменной t символ $1:

На вход этого блока подается сигнал с блока генератора линейно-изменяющегося сигнала ramp, играющего роль блока модельного времени. С выхода блока expression сигнал подается на осциллограф для получения осциллограммы оптимального управления и на блок объекта управления. С выхода блока объекта управления сигнал подается на осциллограф. Получаем осциллограмму ранее рассмотренного сигнала х₁ или он же угол поворота вала двигателя φ. С выхода блока объекта управления сигнал также подается на вход идеального дифференцирующего звена, которое представлено схемой:

В состав звена входят: блок суммирования (вычитания) summing Junctions из библиотеки математических операций Arithmetic, блок идеального интегратора integrator 1/S из библиотеки интегрирующих блоков Integration, блок операции деления из библиотеки математических операций Arithmetic /, два блока масштабирования из библиотеки математических операций Arithmetic с коэффициентами передачи равными 1 (по умолчанию), блок задания переменных variable из библиотеки Annotarions. Входной блок масштабирования моделирует коэффициент усиления идеального дифференцирующего звена, выходной упрощает компоновку схемы и не моделирует никакой части идеального дифференцирующего звена. Сигнал с интегратора подается на вход блок суммирования со знаком минус. Чтобы сформировать знак минус на входе блока необходимо при нажатой клавише Ctrl подвести курсор мыши к нижнему входу блока и в момент смены образа курсора на стрелку ↑ нажать правую кнопку мыши. Вычисление производной осуществляется конечно-разностным методом, для чего в модели присутствует блок $time Step, задающий временной шаг моделирования равный 0,001. Для его создания щелкнем правой кнопкой мыши по блоку задания переменных variable. Появится окно настроек:

Нажмем на стрелку, в появившихся строках выберем строку $time Step.

Запускаем процесс моделирования и получаем осциллограммы оптимального управления и фазовых координат:

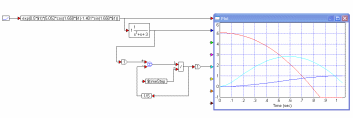
Соберем модель для получения осциллограммы изменения функционала за период работы системы оптимального управления:

Схема содержит блок Мathcad с одним входом и одним выходом. В нем записано выражение функционала, который является выходным сигналом out0. Входной сигнал, поступающий с генератора модельного времени, является переменной t в функционале t := in0. Установим в осциллографе масштабную сетку, верхний предел по оси У равный 13 и нижний – 0. Включим процесс моделирования и получим осциллограмму:

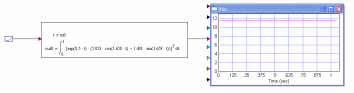
Подадим на вход объекта управления управляющие сигналы различных видов и оценим, будет ли решаться поставленная задача: достижение требуемого угла поворота вала двигателя с последующей остановкой. Подадим линейно-изменяющееся управление и получим:

Поставленная задача не решается данным видом управления. Подадим параболическое управление:

Это управление также не решает задачу. Исследования можно продолжить и для других видов управлений и очевидно вывод будет тот же.