Министерство образования Республики Беларусь УО «Брестский государственный политехнический колледж»

Отчёты

по выполнению лабораторных работ

по дисциплине: «Радиотехника»

Руководитель (преподаватель)

В.Н. Щепёрка

(инициалы, фамилия)

Выполнил учащийся

С.А. Дмитрук

(инициалы, фамилия)

2013г

Лабораторная работа №1

Тема: Исследование гармонических и амплитудно-модулированных сигналов

Цель: Научиться измерять параметры и спектральные характеристики сигналов, оценивать влияние формы сигналов на их спектральные характеристики и делать выходы из полученных результатов.

Оборудование: ПЭВМ, компьютерная программа «Спектр анализатор», тестовая программа «My Test», генератор сигналов, осциллограф, мультимедиа проектор.

1. Краткие теоретические сведения

В радиотехнических каналах используются различные устройства, предназначенные для преобразования сигналов. Основными элементами этих устройств являются генераторы и усилители.

Электронными генераторами называются устройства для создания электрических колебаний определенной частоты, амплитуды и формы.

Колебания появляются в результате преобразования энергии, подключенных к генератору, источников постоянного и переменного токов.

Частоты и форма колебаний определяются свойствами и параметрами цепей генераторов. По форме колебания могут быть синусоидальными, пилообразными, прямоугольными, модулированными по амплитуде ,частоте, фазе и др.

Поскольку реальные физические процессы протекают во времени, то в качестве математической модели сигнала, представляющего эти процессы, используют функции времени, отражающие изменения физических процессов. Все сигналы можно разделить на детерминированные и случайные.

Детерминированным называется колебание, которое может быть описано с помощью определенной функции времени, т.е. его значение известно в любой момент времени. Детерминированные сигналы разделяются на периодические и непериодические. Периодические сигналы повторяются через равные промежутки времени, называемые периодом Т, и не имеют ограничения по времени. Непериодический сигнал имеет начало и конец.

Частоту повторения сигналов можно рассчитать по формуле:

ƒ 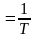· (1)

В радиотехнике широко используется так называемая угловая частота,

ω = 2πƒ, (2)

размерность которой – радиан/секунда или с^-1.

Случайное – колебание, мгновенное значение которого не может быть заранее точно предсказано. Случайным, например, является электрическое напряжение, полученное в результате преобразования речи, музыки, изображения.

Следовательно, передавать по радиоканалу имеет смысл лишь те сообщения, которые заранее точно не предсказываются на приёмном конце линии, и это позволяет утверждать, что только случайные колебания несут информацию.

Случайные колебания описываются с помощью теории вероятности. Иногда, для упрощения расчетов, уравнения случайных колебаний записывают несколько приближенно – как сумму множества детерминированных колебаний. С этой точки зрения сигналом можно называть не только случайные, но и детерминированные колебания.

Чтобы произвести анализ прохождения сигнала через радиотехнические цепи необходимо представить его в необходимой математической форме. В теории сигналов широкое представление нашли два способа их математического и физического представления: временной и спектральный, т.е. сигнал можно рассматривать как функцию времени или частоты. Выбор того или иного способа связан с удобством операции над сигналом.

Любой периодический сигнал произвольной формы разлагается в ряд Фурье, т.е. на бесконечное большое число гармонических составляющих:

постоянную составляющую U₀ (нулевую гармонику), равную среднему значению сигнала за период;

первую гармонику u₁ (t), имеющую амплитуду U_1m , угловую частоту ω₁ = ω, начальную фазу Ψ₁;

вторую гармонику с амплитудой U_2m , с угловой частотой ω₂ = 2 ω, начальной фазой Ψ₂;

третью гармонику и т.д.

Во временном представлении периодический сигнал можно представить рядом Фурье вида:

u (t) = U₀ + 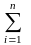U_nm sin(nωt + ψ _n) . (3)

Тогда спектр сигнала – это совокупность гармонических составляющих сигнала.

Спектр сигнала бывает амплитудно – частотный (АЧС) и фазо – частотный (ФСЧ). Спектры изображаются диаграммами, где по оси абсцисс откладывается угловая частота ω или частота гармонических составляющих сигнала ƒ = ƒ_{n ,} а по оси ординат – для каждой n-ой гармоники откладываются отрезки, длина которых равна их амплитуде U_mn для АЧС или начальной фазе ψ _n для ФЧС. Понятно, что спектр периодических сигналов не сплошной, а линейчатый (дискретный), т.е. между соседними линиями спектра есть просветы, шириной, равной частоте повторения (следования) сигнала.

Из (3) следует, что если сигнал представляет собой синусоиду (одну гармонику), то его во временной области можно представить в виде

u (t) = U_m sin(ωt + ψ) . (4)

АЧС такой синусоиды представляет собой одну спектральную составляющую – отрезок, длина которого равна U_m, расположенный на оси частот с частотой ω.

Для несущего гармонического сигнала добавляют индекс «0» для амплитуды и частоты (U_оm, ω₀, ƒ₀).

Вид гармонического сигнала и его АЧС показан на рисунке 1,а.

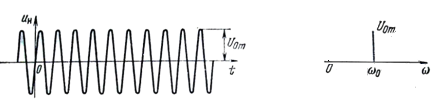
Рисунок 1 – Временные и спектральные диаграммы гармонического сигнала несущей частоты

Под модуляцией в радиотехнике понимается процесс, при котором один или несколько параметров (амплитуда, частота или фаза) несущего колебания изменяется по закону передаваемого сообщения. Получаемые в процессе модуляции колебания называют радиосигналами. В зависимости от того, какой из названных параметров несущего гармонического колебания подвергаются изменению, различают два основных вида аналоговой модуляции: амплитудную (АМ) и угловую. Последний вид модуляции, в свою очередь, разделяется на частотную (ЧМ) и фазовую (ФМ).

В процессе осуществления амплитудной модуляции несущего колебания

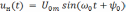
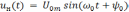(5)

его амплитуда должна изменяться по закону

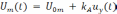, (6)

где U_0m – амплитуда несущего колебания;

k_А – безразмерный коэффициент пропорциональности;

ψ₀ – начальная фаза;

φ(t)=ω₀(t)+ψ₀ – полная (текущая или мгновенная) фаза;

u_у(t) – управляющий (модулирующий) сигнал.

Пусть управляющий (модулирующий) сигнал изменяется по гармоническому закону (тональная модуляция от слова тон – звук одной частоты).

Рассмотрим временные и спектральные диаграммы напряжения управляющего сигнала u_у(t) и радиосигнала u(t) (рисунок 2).

Рисунок 2 – Временные (а) и спектральные (б) диаграммы управляющего и

радиосигналов при амплитудной модуляции гармоническим напряжением

При тональной модуляции управляющим сигналом является синусоида, т.е. u_у(t) меняется по гармоническому закону с некоторой угловой частотой Ω=2πF (F=1/T) относительно постоянной составляющей управляющего сигнала U₀ (рисунок 2, а верхний график). Предположив, что в начальный момент времени t = 0, u_у(t) проходит через максимум, мгновенное значение управляющего сигнала можно представить в виде:

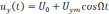, (7)

где U_ym – амплитуда переменной составляющей управляющего сигнала. АЧС управляющего сигнала содержит две спектральные составляющие: «нулевую» с амплитудой U₀ и на частоте Ω с амплитудой U_ym (рисунок 2, б верхний график).

В процессе амплитудной модуляции (АМ) должна соблюдаться прямая пропорциональность между приращениями амплитуды и мгновенного значения управляющего сигнала. Тогда амплитуду U_m радиосигнала можно определить из выражения

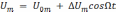, (8)

где ΔU_m – максимальное приращение амплитуды радиосигнала относительно его исходного значения U_0m (ΔU_m = k_АU_ym).

Умножив U_m на высокочастотное заполнение в виде sinω₀t, получим выражение для мгновенного значения АМ радиосигнала

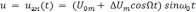. (9)

На временной диаграмме (рисунок 2, а нижний график ), изображенной согласно этому выражению, огибающая радиосигнала, т.е. воображаемая кривая, которая очерчивает границы изменения амплитуды радиосигнала, имеет вид косинусоиды ΔU_mcosΩt.

Раскрыв (9) учтя тригонометрическое произведение cosΩt на sinω₀t, получим

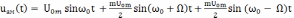, (10)

где m – коэффициент модуляции.

m =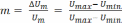 ΔU_m/ U_0m = (U_{m макс} - U_{m мин})/( U_{m макс}+ U_{m мин}). (11)

U_0m = (U_{m макс} + U_{m мин})/2 (12)

Коэффициент модуляции показывает, какую часть от амплитуды напряжения несущей частоты U_0m составляет приращение амплитудно-модулированного напряжения ΔU_m. Когда нет модуляции, то ΔU_m =0. При ΔU_m=U_0m, m = 1 и амплитуда сигнала изменится от U_{m мин} =0 до U_{m макс} =2 U_0m.

Если же m > 1, то происходит перемодуляция, которая приводит к искажению формы амплитудно-модулированного сигнала.

Из уравнения (10) вытекает, что если синусоидальное колебание несущей частоты ω₀ промодулировать по амплитуде гармоническим управляющим сигналом с частотой Ω, то в результате получается несинусоидальное колебание, которое состоит из трех синусоидальных.

АЧС такого радиосигнала изображается тремя вертикальными обрезками (рисунок 2, б нижний график ), причем симметричные линии боковых частот расположены по обе стороны от линии несущей частоты. Они имеют амплитуды .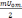

На рисунке 3 показаны временные и спектральные диаграммы напряжений несущей частоты u_н , верхней боковой частоты u_вб, нижней боковой u_нб, результирующего радиосигнала и, равного сумме мгновенных значений напряжений u_н, u_вб, u_нб. Итак, изменение амплитуды радиосигнала происходит в результате того, что к гармоническим колебаниям несущей частоты прибавляется гармонические колебания боковых частот.

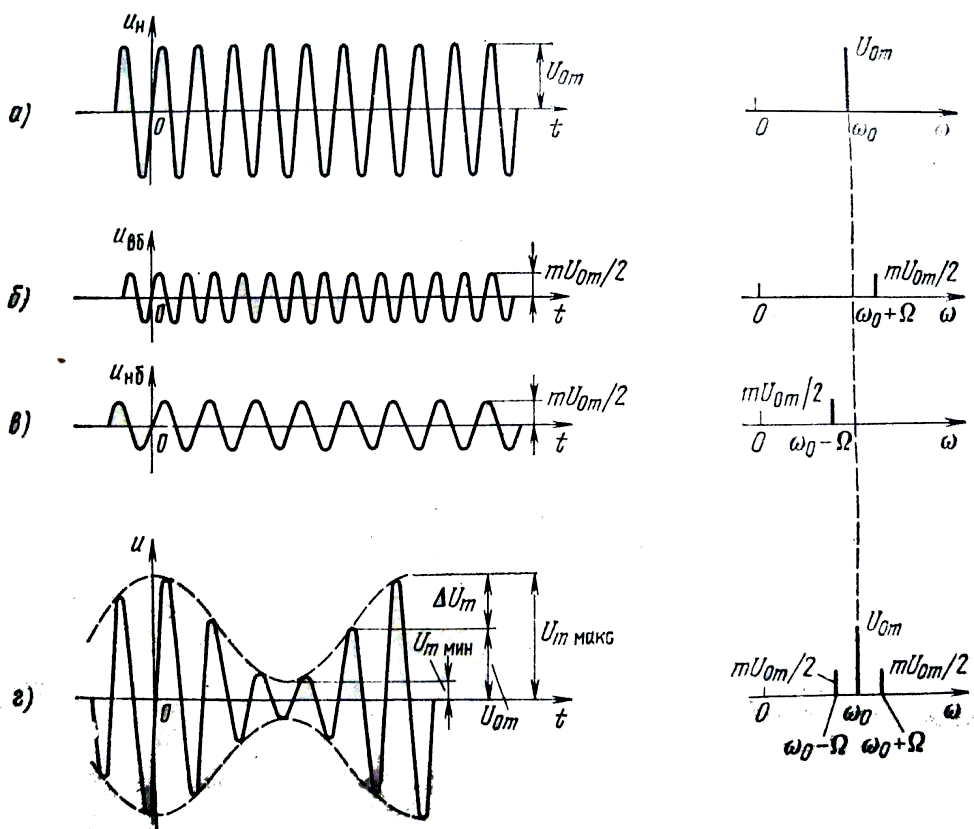
Рисунок 3 – Временные и спектральные диаграммы составляющих

несущей частоты (а), верхней (б) и нижней (в) боковых частот и результирующего

АМ сигнала (г)

Ширина спектра АМ колебания Δω_сп – это область частот между крайними гармониками спектра. При гармоническом управляющем сигнале

Δω_сп = 2Ω (Δ¦_сп=2F). (13)

Спектры, полученные на рисунках 1,2,3, являются линейчатыми и относятся к периодическим сигналам не ограниченным во времени.

Если сигнал ограничен по времени, то его спектр из линейчатого переходит в сплошной, т. е. «растягивается» по оси частот (см. рисунок 4). При этом ширина спектральной составляющей приблизительно равна 1/τ_с, где τ_с – длительности сигнала.

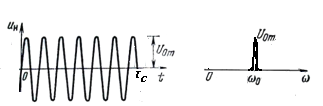
Рисунок 4 – Временные и спектральные диаграммы гармонического

сигнала, ограниченного во времени

Обычно управляющий сигнал имеет сложную структуру, т.е. в нем множество гармонических составляющих, каждая из которых модулирует несущий сигнал независимо друг от друга.