
- •Эластичность спроса по цене
- •Опрос населения
- •1.1 Понятие и сущность конкурентоспособности продукции
- •1.2 Параметры конкурентоспособности продукции
- •Изучение явлений и процессов – изучение типических представителей.
- •Средняя арифметическая величина.
- •Средняя гармоническая величина.
- •Средняя геометрическая величина
- •Средняя квадратическая величина
- •Изучение явлений и процессов – изучение разнообразия.
- •33. Оценивание параметров при проверке исследовательских гипотез.
- •Проверка статистических гипотез: выбор между реальностью и совпадением
- •Непараметрические методы. Проверка гипотез для порядковых данных и данных не подчиняющихся нормальному распределению
- •Поиск закономерностей для качественных данных.
Непараметрические методы. Проверка гипотез для порядковых данных и данных не подчиняющихся нормальному распределению
Виды шкал:
1. Номинальная (шкала наименований).
2. Порядковая (ранговая, шкала порядка).
3. Интервальная (шкала интервалов).
4. Относительная (шкала отношений).
Неметрические
Номинальная шкала представляет собой конечный набор обозначений для никак не связанных между собой состояний или свойств объекта.
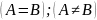
Примеры: цвет, марка автомобиля, пол, профессия, место жительства и т.д.
При обработке экспериментальных данных, зафиксированных в номинальной шкале, непосредственно с самими данными можно выполнять только операцию проверки их совпадения или несовпадения.
Порядковая шкала применяется в тех случаях, когда наблюдаемый (измеряемый) признак состояния имеет природу, не только позволяющую отождествить состояния с одним из классов эквивалентности, но и дающую возможность в каком-то отношении сравнивать разные классы.
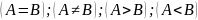
Примеры: Нумерация очередности, неимение знания, призовые места в конкурсе, социально-экономический статус
Метрические шкалы
Интервальная шкала в отличие от предыдущих, качественных, шкал уже является количественной шкалой. Эта шкала применяется, когда упорядочивание значений измерений можно выполнить настолько точно, что известны интервалы между любыми двумя из них.

Примеры: Температура, время, высота местности
Измерения относительной шкале являются «полноправными» числами, с ними можно выполнять любые арифметические действия, здесь присутствуют все атрибуты измерительных шкал: упорядоченность, интервальность, нулевая точка. Величины, измеряемые в шкале отношений, имеют естественный, абсолютный нуль, хотя остается свобода в выборе единиц.
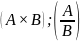
Примеры: Вес, длина, электрическое сопротивление, деньги — величина, природа которых соответствует шкале отношений. Из значений шкалы отношений видно, во сколько раз свойство одного объекта превосходит такое же свойство другого объекта.
Параметрические критерии – критерии, включающие формулы расчета параметров распределения признака (среднее арифметическое и дисперсия). Распределение должно соответствовать нормальному, признак измерен в метрической шкале. (сравнение средних значений по критерию t-Стьюдента, сравнение дисперсий по критерию F-Фишера).
Непараметрические критерии – критерии, не включающие в формулу расчета параметров распределения, не требующие нормальности распределения и основанные на оперировании частотами или рангами.
Преимущества непараметрических методов:
Не нужны предположения о нормальности, могут быть использованы, даже если распределение не является нормальным.
Можно использовать для тестирования порядковых данных
Недостатки:
Данные методы менее статистически эффективны чем параметрические методы
Проверка гипотезы о равенстве медианы некоторому заданному значению
Так как непараметрические методы основаны на использовании рангов упорядоченных данных, они позволяют осуществить проверку гипотезы о медиане генеральной совокупности.
Гипотезы:
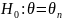 ,
медиана генеральной совокупности
,
медиана генеральной совокупности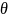 равна известной опорной величине
равна известной опорной величине
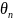
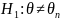 ,
медиана генеральной совокупности
равна известной опорной величине
,
медиана генеральной совокупности
равна известной опорной величине
Единственное условие - выборка из изучаемой генеральной совокупности должна быть случайной
Подсчитываем количество данных, значения которых отличаются от заданного опорного значения , обозначим данное число за m и назовем размером модифицированной выборки.
Используя таблицы или формулу, находим границы для заданного размера модифицированной выборки
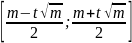
t = 1,96 для уровня значимости 5%
t = 2,576 для уровня значимости 1%
Подсчитываем количество значений, которые лежат ниже заданного опорного значения и сравниваем это число с найденными границами.
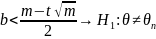
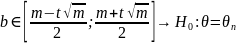
Тестирование различий в двух связанных выборках
Данный тест позволяет сделать вывод о том, является ли связь между X и Y статистически значимой.
Гипотезы:
H0 – вероятность того, что X<Y равна вероятности того, что X>Y
H1 – вероятность того, что X<Y не равна вероятности того, что X>Y
Формируем новую выборку из разностей значений X и Y
Подсчитываем количество значений не равных 0, данное число обозначаем за m, что будет являться размером модифицированной выборки.
Устанавливаем границы для данного размера модифицированной выборки, используя таблицы или формулу
t = 1,96 для уровня значимости 5%
t = 2,576 для уровня значимости 1%
Подсчитываем количество отрицательных значений и сравниваем с полученными границами
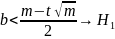
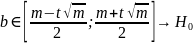
Проверка значимости различия двух независимых выборок
Критерий суммы рангов Вилкоксона и U-критерий Манна-Уитни – два разных способа непараметрического тестирования двух независимых выборок, которые дают один и тот же результат. Критерий суммы рангов Вилкоксона основан на сумме общих рангов одной из выборок, а в основе U-критерия Манна-Уитни лежит количество способов, с помощью которых можно в одной выборке найти значение, превышающее значение в другой выборке. Более простой способ заключается в использовании среднего ранга двух выборок.
Данный тест позволяет сделать вывод о том, взяты ли две независимые выборки из генеральных совокупностей с одинаковым распределением.
Условия:
Выборки являются случайными из соответствующих генеральных совокупностей
Объемы выборок превышают 10
Гипотезы:
H0 – две выборки принадлежат генеральным совокупностям с одинаковым распределением
H1 – две выборки принадлежат генеральным совокупностям с разным распределением
Объединяем данные обеих выборок и упорядочиваем в порядке возрастания для получения рангов. Если имеются одинаковые значения, то им присваивается одинаковый ранг, равный среднему значению рангов этих значений.
Находим среднее значение всех рангов для каждой выборки
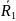 и
и
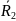
Вычисляем стандартную ошибку
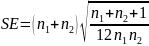
Вычисляем значение t статистики
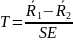
Делаем вывод:
If T<1,960 → H0
If T>1,960 → H1
