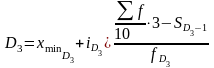Изучение явлений и процессов – изучение типических представителей.
Зачастую при проведении маркетинговых исследований необходимо проанализировать выборки с достаточно большим объемом. Так как исследование каждой единицы совокупности является проблематичным и затратным, пытаются выделить наиболее характерные признаки единиц совокупности, описать типической представителя выборки и тем самым сделать выводы о генеральной совокупности.
Наиболее частый показатель, используемый для характеристики типического представителя генеральной совокупности, является средняя. Например, фирма интересуется, сколько в среднем тратит на спортивные товары жители города.
При вычислении средних погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами, и находят выражение общие и закономерные черты, свойственные всей совокупности в целом.
Средняя арифметическая величина.
Простая:
.
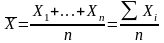Эта формула применяется в тех случаях, когда исходные данные не сгруппированы по какому-то признаку) и каждой единице совокупности соответствует определенное значение признака, либо, когда все частоты равны между собой.
Взвешенная:
.
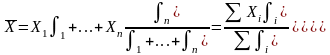Эта формула применяется в тех случаях, когда исходные данные сгруппированы, и каждой группе единиц совокупности соответствует определенное значение признака.
Средняя гармоническая величина.
Простая:
.
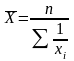Взвешенная:
,
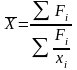где Fi=xi*fi.
Эта формула применяется в тех случаях, когда в качестве исходных данных приводятся индивидуальные значения признака и произведения индивидуальных значений признака на соответствующие частоты.
Средняя геометрическая величина
Невзвешенная (простая):
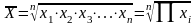,Взвешенная:
.
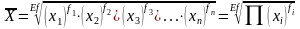Средняя квадратическая величина
Невзвешенная
(простая):
;
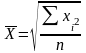Взвешенная:
.
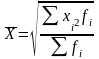Модой называют значение признака, который наиболее часто встречается в исходной совокупности.
В дискретном вариационном ряду Мо является признак, имеющий наибольшую частоту.
В интервальном вариационном ряду мода вычисляется следующим образом:
, где:
-
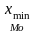нижняя граница интервала, содержащая
Мо;
iMo – величина модального интервала;
fMo – частота модального интервала;
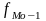- частота интервала,
предшествующего модальному;
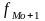- частота интервала,
следующего за модальным.
Медиана – это значение признака при котором исходная совокупность делится на 2 равные части, при этом первая половина совокупности имеет значение признака меньше, чем медиана, а вторая имеет значения признака больше, чем медиана. К примеру, медиана может использоваться для классификации потребителей по уровню доходов.
,
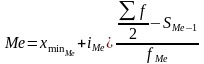где
-
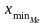нижняя граница медианного интервала
(интервала, содержащего единицу, которая
делит всю совокупность на 2 равные
части);
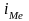- величина медианного интервала;
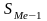- накопленная частота интервала,
предшествующего медианному;
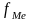- частота медианного интервала.
Квартиль делит исходную совокупность на 4 равные части. Нижний/верхний квартиль представляет 1/4 часть населения с наименьшими/наибольшими среднедушевыми доходами.
Квартиль вычисляют
по формуле:
;
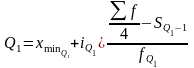Дециль делит исходную совокупность на 10 равных частей. Например, нижний дециль представляет 1/10 часть населения с самыми низкими доходами, а верхний дециль представляет 9/10 часть населения с самыми высокими доходами.
Дециль вычисляют
по формуле:
