§ 4. Случайные величины, случайные элементы.

4.1. Пусть (,F) и (R¹,(R¹)) - измеримые пространства.

Определение. Действительная функция определенная (,F), принимающая значения в R¹ называется F – измеримой или случайной величиной, если: (R¹) F (то есть, прообраз является измеримым множеством в ).

Если =(Rⁿ,(Rⁿ)), то (Rⁿ) – измеримые функции называются борелевскими.

Простейшим примером случайной величины является

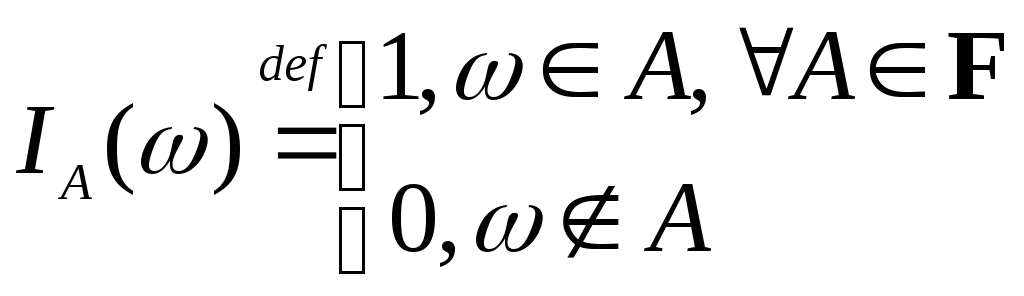
Определение. Случайная величина представимая в виде

(2)

где F называется дискретной. Если число слагаемых в сумме в (2) конечно, то случайная величина называется простой.

Замечание. Случайная величина это некоторая характеристика эксперимента, результаты которого зависят от случая . Требование измеримости важно. Действительно, если на (,F) задана вероятностная мера Р и , то в этом случае можно говорить о вероятности события, состоящего в том, что значение случайной величины принадлежит борелевскому множеству В.

Определение. Вероятностная мера на (R,(R)) с , (R¹), называется распределением вероятностей случайной величины на (R,(R)).

Определение. Функция Р, где R¹, называется функцией распределения случайной величины .

Замечание.Для дискретной случайной величины мера сосредоточена не более чем в счетном числе точек и может быть представлена в виде ,

где .

Определение. Случайная величина называется непрерывной, если ее функция распределения непрерывна. Случайная величина называется абсолютно непрерывной, если ,R¹.

4.2. Вопрос: Когда функция обозначаемая является случайной величиной? Для этого надо проверить условие F для любого (R¹).

Лемма 7. Пусть  – некоторая система множеств такая, что ()=(R¹). Для того, чтобы была F - измеримой необходимо и достаточно, чтобы F для всех .

Доказательство. Необходимость очевидна.

Достаточность. Пусть  – система борелевских множеств , для которых F. Известно, что:

i), ii), iii)=.

Отсюда следует, что система  – является -алгеброй, значит (R¹) и (), следовательно =(R¹).

Лемма 8. Пусть : R¹R¹ - борелевская функция, а - случайная величина. Тогда сложная функция (то есть ) - случайная величина.

Доказательство. Действительно

,

так как (R¹), (R¹).

Доказательство закончено.

Определение. Функция на (,F) со значениями в = называется расширенной случайной величиной, если: для (R¹) F.

Теорема 9. 1) Для любой случайной величины найдется последовательность простых случайных величин таких, что и при для всех .

2) Если случайная величина , то найдется последовательность простых случайных величин таких, что для всех .

Доказательство. Начнем с пункта 2). Положим , и

непосредственной проверкой, устанавливается, что для всех. Отсюда следует и доказательство пункта 1) так как можно представить в виде , где .

Теорема 10.Пусть - последовательность расширенных случайных величин и = . Тогда -расширенная случайная величина.

4.3. Определение. Пусть - случайная величина. Пусть множества из вида , (R¹) . Наименьшую -алгебру порожденную такими множествами называют -алгеброй, порожденной случайной величиной и обозначают ее через F^.

Если - борелевская функция, то из леммы 7 следует, что - случайная величина, причем F^ - измерима. Оказывается, справедливо и обратное утверждение.

Теорема 11. (Бореля). Пусть –измеримая случайная величина. Тогда найдется борелевская функция : R¹R¹ такая, что , т.е. для каждого . (Докажите самостоятельно.)

4.4. Определение. Пусть (,F) и (E,) - измеримые пространства. определенная на принимающая значения в E называется F/ –измеримой функцией или случайным элементом (со значениями в E  F). (3)

Примеры случайных элементов:

1) Если (E,) = (R¹,(R¹)), то определение случайного элемента совпадает с определением случайной величины.

2) Пусть (E,) = ( Rⁿ,(Rⁿ)). Тогда случайный элемент называется n - мерным случайным вектором. Если - проекция Rⁿ на -ую координату, то =, где . Ясно, что - обычные случайные величины. Действительно, для (R¹) R¹,..,R¹,R¹R¹}= (R¹R¹R¹R¹)F.

Определение. Упорядоченый набор случайных величин будет называться - мерным случайным вектором.

В соответствии с этим определением всякий случайный элемент со значениями в Rⁿ будет - мерным случайным вектором. Справедливо обратное утверждение: всякий n- мерный случайный вектор = есть случайный элемент в Rⁿ. Действительно, если (R¹),, то 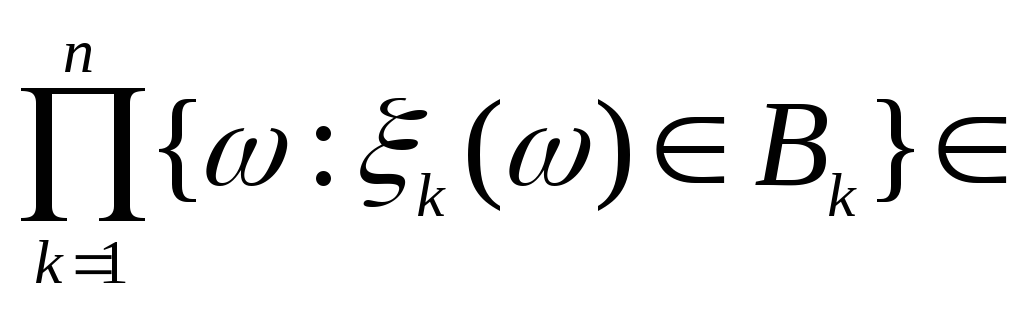F, то наименьшая -алгебра, порожденная всеми совпадает с (Rⁿ). поэтому для (Rⁿ) F.

3) Пусть (E,) = (R^Т,(R^Т)), Т – подмножество числовой прямой. В этом случае всякий случайный элемент представим в виде с называется случайной функцией с временным интервалом Т.

4.5. Определение. Пусть R¹. Совокупность называется случайным процессом с временным интервалом Т. Если , то - называется случайным процессом с дискретным временем или случайной последовательностью. Если , то - называется случайным процессом с непрерывным временем.

Определение. Пусть - случайный процесс. Для каждого функция - называется реализацией или траекторией процесса, соответствующего исходу .

Определение. Пусть - случайный процесс. Вероятностная мера Р на (R^Т,(R^Т)) с PP,(R^Т) называется распределением вероятностей процесса Х.

Определение. Вероятностная мера PP, где (Rⁿ), , называется конечномерными распределениями вероятностей случайного процесса , а n-мерная функция распределения , где , называется конечномерными функциями распределения процесса .

4.6. Определение. Пусть (,F,P) - вероятностное пространство и набор () - измеримых пространств, где - произвольное множество. Будем говорить, что- измеримые функции независимы в совокупности, если для любого конечного набора элементы - независимы, т.е. для PP.

Теорема 12. Для того, чтобы случайные величины были независимы в совокупности, необходимо и достаточно, чтобы для любого Rⁿ , где . Докажите самостоятельно.