Лекция № 5
Определение 1. Марковская цепь { n } называется однородной, если для n ≥ 0
Р ( n, n+1) = P; Р = ( P i j, i, j Х) – матрица вероятностного перехода (МВП) за один шаг.
Тогда P (n, m) = P m- n, m > n.
Иначе : P ( k ) = ( Рj i ( k), i , j Х ) - МВП за k шагов.
Тогда Р ( k ) = Pk .
Задавая матричные Р , мы можем задавать все характеристики.
В дальнейшем будем рассматривать только однородные марковские цепи.
Классификация состояний
Определение 1. Состояние j Х достижимо из i Х
(
i
→ j
), если существует m
> 0 : Р i j
( m
) > 0.
j
Иначе: Существует такая цепочка состояний i1, i 2 , …, t m-1 X
i Р i, i1 > 0, Р i 1 , i 2 > 0, …, Р i m-1, j > 0.
(эта цепочка состояний ( i, i 1, …, i m-1, j ) называется
путем из i в j ).
Определение 2. Если имеет место двойная связь, т.е i → j, j → i, то состояния называются сообщающимися и записывают i ~ j .
Замечание. i → j транзитивно, т.е. если i → j, j → k, то i → k.
Определение 3. Множество Е всех сообщающихся между собой состояний называется классом или блоком.
Все множество состояний можно, некоторым образом, разбить на непересекающиеся классы:
jI
Число классов может быть счетно.
Определение 4. Класс Е будем называть замкнутым, если из этого класса нельзя перейти в состояние вне его:
i
E, j
E : Рj
i
=
0
Переходы возможны только внутри этого класса.
Замкнутый класс из одного состояния называется поглощающее состояние, т.е.
1
Р
i
i =
1, Р
j
i =
0, j ≠ i i .
Определение 5. Если все множество состояний состоит из одного класса ( т.е. все состояния сообщающиеся), то марковская цепь называется неприводимой (неразложенной).
Свойства состояний
-
С
ущественность.
j
О
пределение
1. Состояние
i
Х будем называть несущественным,
если найдется
такое
состояние j
≠ i,
что существует путь из i
в j
( i
→ j
), но не существует пути обратного (
j
→ i
).
i
j
Состояние i Х будем называть существенным, если для j ≠ i
такого, что i → j, j → i.
i
Теорема 1. (альтернатива солидарности)
В одном классе все состояния либо существенны, либо несущественны одновременно.
Теорема 2. Класс Е замкнут тогда и только тогда, когда он существенный, т.е. все его состояния существенны (доказательство от противного).
-
Возвратность.
Пусть есть однородная цепь Маркова { n , n ≥ 0 }, Р ( n ) = Р j i ( n), i , j Х – МВП за n шагов, начальное состояние 0 = i Х фиксировано. Обозначим
Vi (n ) = Р ( 1 ≠ i , 2 ≠ i , … , n-1 ≠ i , n = i / 0 = i )
вероятность впервые вернуться из i в себя на шаге с номером n.
При условии 0 = i событие
Вn = ( 1 ≠ i , 2 ≠ i , … , n-1 ≠ i , n = i ) – несовместны.
Вn ∩ Вm = Ø , m ≠ n
∞
n=1
B - цепь ни разу не вернется в исходное состояние.
{ В1, В2, …, B } – полная группа несовместимых событий.
∞ ∞
Введем вероятность Vi = ∑ Vi ( n ) = ∑ P ( Вn | 0 = i ) =
n=1 n=1
∞
n=1
за конечное число шагов.
Определение. Состояние i называется возвратным, если Vi = P ( В | 0 = i ) = 1 и
невозвратным в противном случае, т.е. Vi < 1.
Замечание.
Состояние i называется
возвратным,
если Р ( В |
0 =
i )
= 0 и
невозвратным,
если Р ( В |
0 =
i )
> 0
Лекция № 6
Теорема. ( о необходимых и достаточных условиях возвратности)
∞
Состояние i марковской цепи возвратно ↔ , когда ряд ∑ Рi i ( n ) = ∞ из
n=1
вероятности состояний расходится.
Доказательство. Событие Вk = ( 1 ≠ i , … , k-1 ≠ i , k = i ) при условии
0 = i, k = 1, 2, …, n
Вn + 1 = ( 1 ≠ i , … , n ≠ i )
за n шагов цепь ни разу не вернется в начальное состояние i. Для
фиксированного n { В1, …, Вn , Bn +1 }- полная группа несовместных
событий.
А = ( 0 = i )
Формула полной вероятности:
n+1
Р (А) = ∑ P ( A | Вk ) P ( Вk ) ( 1 )
k=1
Заметим, что в ( 1 ) вероятности вводились:
P
( Вk )
= P (
1
≠
i , …
,
k-1
≠ i ,
k
=
i
/
0
=
i ) = Vi
( k ), k
= 1, n – 1
P
( A | Вk )
= P (
n
=
i ,
0
=
i ,
1
≠
i, …
,
k-1
≠ i ,
k
=
i )
= { в силу марковского свойства } = P (
n
=
i |
k
=
i ) = Pi
i ( n – k ), k
= 1, n – 1
P ( A | Вn ) = P ( n = i | n = i ) = 1
P ( A | Вn +1 ) = 0, т.к. эти события несовместны.
P ( A ) = P ( n = i | 0 = i ) = Pi i ( n )
О
бозначим:
Uk =
Pi i
( k ), k
= 1, n – 1
U0 = 1 - вероятность за 0 шагов
Vi (о) = 0 (доопределили)
Тогда из соотношения (1) получим:
Un = U0 Vi ( n ) + U1 Vi (n - 1) + …+ Un - 1 Vi (1) + Un Vi ( о ) ( 2 )
n = 1, 2…
Обозначим Vi ( k ) = V k
Введем следующие функции:
∞ ∞
U ( z ) = ∑ Uk Zk ; V ( z ) = ∑ Vk Zk ;
n=0 n=0
производящие.
В соотношении ( 2 ) обе части умножаем на Zn и просуммируем по n:
U( z ) - U0 = U ( z ) V ( z ) ( 3 )
Замечание. Если хотим перемножить две суммы, то получим ряд:
U (z) V (z) = ( ∑ Uk Zk ) ( ∑ Vk Zk ) = ∑ Zk ( U0 Vn + U1 V n - 1 + …+ Un V0 )
k k n
Из ( 3 ):
U
( z
)
=
1
( 4
)
1 - V (z)
Заметим, что получили при переходе к пределу
∞ ∞ ∞ ∞
( 5 ) lim U ( z ) = lim ∑ Un Zn = ∑ Un = 1 + ∑ Un = 1 + ∑ Pi i ( n )
z →1 z →1 n=0 n = 0 n = 1 n =1
∞ ∞
( 6 ) lim U ( z ) = lim ∑ Vn Zn = ∑ Vn = V = P ( B / 0 = i )
z →1 z →1 n=0 n = 0
Переходя к пределу в ( 4 ), с учетом ( 5 ) и ( 6 ) получаем
∞ 1
1
l
im
U ( z ) = 1 + ∑ Pi i
( n )
= lim
1 –
V( z ) = 1 ─ V
z →1 n = 1 z →1
∞
Тогда V = 1 ↔ ∑ Pi i ( n ) = ∞
n = 1
Лемма ( Бореля – Кон Телли )
Пусть { A n, n ≥ 1 } последовательность произведенных событий,
ρ n = Р (A n ), n ≥ 1. Если ряд из вероятностей
∞ ∞
∑ ρ n = ∑ Р (A n ) < ∞
n = 1 n = 1
сходится, то с вероятностью равной 1 произойдет лишь конечное число событий из данной последовательности. (без доказательства)
Теорема. (о числе возвращений; возвратное и невозвратное состояние соответственно).
Если исходное состояние i марковской цепи является возвратным, то с вероятностью равной 1 наша цепь бесконечно много раз возвратится в это состояние. Если исходное состояние i является невозвратным, то с вероятностью равной 1 марковская цепь лишь конечное число раз возвратится в исходное состояние.
Обозначим χ - число возвращений марковской цепи в исходное состояние i.
Р ( χ = ∞ | 0 = i ) = 1, если i – возврат.
Р ( χ < ∞ | 0 = i ) = 1, если i – не возврат.
Утверждение теоремы означает:
Если i – не возврат, то с вероятностью равной 1, начиная с конечного момента времени, цепь никогда больше не вернется в исходное состояние i.
Доказательство.
Обозначим υ1 - случайное число шагов до первого возвращения в исходное состояние i.
υ n - случайное число шагов до n - того возвращения.
Если число возвращений конечно и равно n, то υ n < ∞, υ n+1 = ∞.
( χ = n ) = (υ n < ∞, υ n+1 = ∞ ).
Рассмотри случайный интервал времени [ 0, υ1 ], [ υ1, υ2 ], … [ υ n+1, υ n ] , …
В эти моменты времени цепь возвращается в исходное состояние.
Тогда υ = i, υ1 = i , … υ n = i .
В эти моменты цепь n обладает свойствами марковости и ее состояние зависит от начального, ее поведение не зависит от прошлого. Состояние цепи совпадает с начальным.
Поскольку поведение марковской цепи определяется ее начальным состоянием и МВП, то все характеристики марковской цепи в момент возвращения совпадают с характеристиками этой цепи в начальный момент времени.
В частности, случайные величины υ1 = υ1 - υ , υ2 - υ1 ,…, υ n - υ n - 1
независимы и одинаково распределены.
Лекция № 7
0 =
i
┬─────┬──────┬─────┬─────┬─────
0 υ1= n1 υ2= n2 … υ n= n n υ n+1 = n n+1
Заметим далее (υ 1 = ∞ ) – процесс ни разу не вернулся в начальное состояние.
∞
(υ 1 = ∞ ) = ∩ ( k ≠ i ) = B ( см. выше )
k = 1
(υ 1 < ∞ ) = B – момент конечен
Р (υ 1 < ∞ ) = Р ( В ) = V – вероятность возвращения.
Исходя из этих замечаний делаем следующий вывод:
( 1 ) Р (υ 1 < ∞ ) = Р (υ 2 < ∞ | υ 1 < ∞ ) = … = Р (υ k +1 < ∞ | υ k < ∞) =, Vk ≥ 1.
Кроме того, имеет место такая связь:
( 2 ) ( υ k +1 < ∞ ) ≤ ( υ k < ∞ ), k ≥ 1.
( если процесс вернулся в k +1 шаг, то он вернулся и в k -тый шаг ).
Тогда Р ( υ 2 < ∞ ) = Р ( υ 2 < ∞ , υ 1 < ∞ ) из соотношения ( 2 ).
По определению условия вероятности имеет место формула:
Р ( υ 2 < ∞, υ 1 < ∞ ) = Р (υ 2 < ∞ | υ 1 < ∞ ) Р ( υ 1 < ∞ ) ( 3 )
Тогда из ( 3 ) следует: (1)
Р ( υ 2 < ∞ ) = Р (υ 2 < ∞ | υ 1 < ∞ ) Р ( υ 1 < ∞ ) = V 2
Аналогично для k:
Р (υ k +1 < ∞ ) = Р (υ k +1 < ∞ | (υ k < ∞) P (υ k < ∞) = V k +1
Имеем общее свойство P (υ k < ∞) = V k, k ≥ 1.
Если состояние i невозвратно (т.е. V < 1 по определению), то можно составить ряд:
∞ ∞
∑ Р ( Vk < ∞ ) = ∑ Р Vk < ∞ .
k = 1 k = 1
Тогда по лемме Бореля – Кон Телли происходит конечное число событий ( υ k < ∞ ), с вероятностью равной 1. Т.е. получилось утверждение теоремы для случая невозвратности.
Вторая часть доказательства.
Пусть i возвратно, лемму применить нельзя, и не знаем, что будет, хотя ряд конечно расходится.
Тогда рассмотрим Р ( υk < ∞ ) = υ k = 1, k ≥ 1.
Для k мы рассмотрим, но надо посмотреть пересечение.
Пусть χ - число возвращений в состояние i. Тогда
∞
( χ = ∞ ) = ∩ ( υk < ∞ ) (по определению случайных величин ).
k = 1
Отметим ( υ1 < ∞ ) ≥ ( υ2 < ∞ ) ≥ … ≥ ( υk < ∞ ) ≥ ( υk+1 < ∞ ) ≥ …
Воспользуемся теоремой из классической теории вероятностей ( свойства непрерывности вероятности ) ∞
Р ( χ = ∞ ) = lim ( υk < ∞ ) = lim υ k = 1
k→ ∞ k→∞
Теорема ( о связи свойств существенности и возвратности)
Всякое возвратное состояние является существенным. В конечном классе состояний верно и обратное, всякое существенное состояние является возвратным.
В конечном классе два этих свойства эквивалентны, но в счетном – нет.
Доказательство. 1) Пусть некоторое состояние i несущественно. Тогда по определению для некоторого состояния j ≠ i найдется такое число m > 0,
что Р i j ( m ) > 0, но Р j i ( k ) = 0, k = 1, 2, …
Обозначим А i j ( m ) - событие, что процесс переходит из i в j за “m” шагов
Р i j ( m ) = Р ( А i j ( m ) ) > 0.
∞
В
= ∩ ( k
≠ i ) - событие, что процесс ни разу
не вернулся в начальное состояние i
.
k = 1
Установим связь между А j i ( m ) и В.
Если состояние несущественно, то имеет место следующее:
А i j (
m ) ≤ В.
Т
огда
из этого отношения следует: Р ( А i j
( m )
) ≤ Р ( В ).
Р
i j ( m
) ≤ Р ( В ) = 1 - V –
вероятность возвращения ↔ V
≤ 1 - Р i j
( m ) < 1 (т.к Р i j
( m ) > 0 ).
Итак, V < 1, т.е. i невозвратно.
Получилось, что если состояние несущественно, то тогда оно невозвратно, отсюда следует ( возвратность следовательно существенность ).
2) Пусть Е – конечный класс существенных состояний.
Докажем от противного. Пусть в этом классе Е найдется к.– и. невозвратное состояние. Тогда по альтернативе солидарности для свойства возвратности все состояния в Е должны быть тоже невозвратными, т.е. Е – невозвратный класс. По m
(о существенном классе) Е – замкнутый.
Вывод: Е – конечный, невозвратный и замкнутый класс.
Но по m (о числе возвращений), если состояние невозвратно, то процесс может лишь конечное число раз возвращаться в это состояние. Поскольку Е – конечный класс, то в этом классе процесс может находиться лишь конечное время ( с вероятностью 1 ): это свойство противоречит замкнутости класса Е. Получили противоречие, отсюда следует, конечный, существенный класс будет и возвратным.
Лекция № 8
Теорема. (альтернатива солидарности для свойств возвратности)
В одном классе все состояния либо возвратны, либо невозвратны одновременно.
Доказательство. Пусть два состояния сообщаются ( i ~ j ) i , j Е – класс.
По определению сообщающихся состояний m > 0, n > 0 Р j i (m) = α > 0; Р j i (n) =β> 0
Тогда для k > 0 (m, n, k – целые).
Р i i ( k + m + n ) ≥ Р i j ( m ) Р j j ( k ) Р j i ( n ) = α , β Р j j ( k ) ( 1 )
Р j j ( k + m + n ) ≥ Рj i ( n ) Р i i ( k ) Р i j ( m ) = α , β Р i i ( k ) ( 2 )
Замечание к ( 1 ) и ( 2 ): Эти свойства основаны на том, что в левой части стоят
вероятности перехода из i в i произвольным образом, в правой части – такие же вероятности, но по части траектории. Аналогичное соотношение можно получить и в уравнении Колмогорова – Чепмена.
Р i j ( k1, k2 ) = ∑ Р i,ℓ ( k1 ) Р ℓ, j ( k2 ) ≥ Р i ,ℓ o ( k1 ) Р ℓ o , j ( k 2 )
ℓX
ℓ0 Х – фиксировано.
Из ( 1 ) и ( 2 ) можно выписать следующее соотношение. Просуммируем по k обе части наших неравенств.
∞ ∞
∑ Р i i ( k + m + n ) ≥ α , β ∑ Р j j ( k ) ( 3 )
k = 1 k = 1
∞ ∞
∑ Р j j ( k + m + n ) ≥ α , β ∑ Р i i ( k ) ( 4 )
k = 1 k = 1
Можно левые части ( 3 ) и ( 4 ) переписать:
∞ ∞ m+n
∑ Р i i ( k + m + n ) = ∑ Р i i ( ℓ ) – ∑ Р i i ( ℓ )
k = 1 ℓ = 1 ℓ = 1
другой способ:
∞ m+n ∞ m+n ∞
∑ Р i i ( k ) = ∑ Р i i ( k ) + ∑ Р i i ( k ) = ∑ Р i i ( k ) + ∑ Р i i ( k + m + n ) ≥
k = 1 k = 1 k = m + n + 1 k = 1 k = 1
( 3 ) m+n ∞
≥ ∑ Р i i ( k ) + α , β ∑ Р j j ( k ) ( 5 )
k = 1 k = 1
∞
n m
∑ Р j j ( k ) = ∑ Р j j ( k ) + ∑ Р j j ( k ) = ∑ Р j j ( k ) + ∑ Р j j ( k + m + n ) ≥
k = 1 k = 1 k = m + n + 1 k = 1 k = 1
( 4 ) m+n ∞
≥ ∑ Р j j ( k ) + α , β ∑ Р i i ( k ) ( 6 )
k = 1 k = 1
∞ ∞
Из соотношения ( 5 ) и ( 6 ) ряды ∑ Р i i ( k ) и ∑ Р j j ( k )
k = 1 k = 1
сходятся или расходятся одновременно следуя теореме о необходимости и достаточности условий возвратности, утверждение теоремы верно.
Замечание по общему характеру эволюции марковской цепи.
Множество всех состояний марковской цепи Х можно разбить на классы, которые будут либо возвратны, либо невозвратны. Возвратные классы непременно будут замкнуты (возвратный → существенный ↔ замкнутый).
Класс невозвратный, конечный будет незамкнут.
В невозвратном конечном классе марковская цепь прибывает лишь конечное время с вероятностью равной 1.
Если все невозвратные классы конечны, то с вероятностью равной 1 на конечном шаге процесс переходит в один из возвратных замкнутых классов, где и остается.
-
Положительность.
Пусть 0 = i Х – начальное состояние, υ 1 , υ 2 , … υ n , … последовательные моменты возвращения в состояние i. Ранее было установлено, что случайные величины υ 1 – 0 = υ 1 , υ 2 – υ 1 , …, υn – υ n – 1 , … - независимые однозначно распределены.
Введем μ i = Μ υ 1 = ( υn – υ n – 1 ) – математическое ожидание времени между последним возвращением в i.
Определение. Состояние i называется положительным, если μ i < ∞,
i - нулевое, если μ i = ∞.
Связь свойств возвратности и положительности
∞
В
= ∩ ( k
≠ i ) , В – возврат b i на
конечном шаге. Но два события:
k = 1
(
υ1 = ∞ ) = В ( по
определению ).
Если
i не возврат, т.е. Р ( В ) =
Р ( υ1 = ∞ ) > 0, то
случайная вероятность υ1
называется несобственной и Μ
υ 1
= ∞.
Т.о. невозвратное состояние является нулевым.
Обратное, вообще говоря, неверно.
Если состояние положительное, то оно возвратно. Обратное верно для конечных классов, т.е. в конечных классах возвратное состояние является положительным.
Теорема. Всякий конечный замкнутый класс является возвратным и положительным.
Иллюстрация:
Все множество состояний Х
только в счет марковской цепи
возвратные
В конечной марковской цепи
положительные
возвратные положительные
в
озвратные
нулевые
(существенные)
невозвратные нулевые
невозвратные (несущественные)
нулевые
Теорема (альтернатива солидарности для положительных состояний)
В одном классе все состояния либо положительные, либо нулевые.
(доказательство см. ниже в теории пределов вероятности перехода).
Пример (случайные блуждания по целочисленным точкам)
I.
Одномерное блуждание
Х = { 0, ± 1, ± 2, …} – все целые числа = Z – множество состояний.
Вероятность перехода марковской цепи по следующему правилу:
p, j = i +
1
1
– р р
Р i j =
q = 1
– p, , j = i – 1
──┴──┴──┴────
0 – в остальных случаях i – 1 i t + 1
Лекция № 9
Исследование свойств марковской цепи
-
В
се
состояния сообщающиеся и образуют один
класс Х.
Пусть j, i – фиксированы, обозначим j – i = m > 0. Тогда вероятность перехода
Р i j ( m ) ≥ Р i, i +1 , Р i +1 , i +2 , …, Р j-1, j = P m > 0.
2. Все состояния существенные ( это следует как из определения, так и из того, что
все состояния образуют один класс).
3. Проверим возвратность. Возьмем начального состояния 0 = i, надо
рассмотреть следующую вероятность Р i i ( m ) - ?
( при четном числе шагов может вернуться в i , а при нечетном – не может).
Р i i ( n ) = C ak k p k q k , n = 2k, k = 1, 2, …
-
, n = 2k + 1, k = 0, 1, 2, …
Замечание. Успех – это движение вправо, неуспех – влево (Бернулли). Вероятность перехода следует из схемы Бернулли или из непосредственных рассуждений.
Состояние i бывает возвратным ↔ ряд
∞ ∞
∑ Р i i ( n ) = ∑ C ak k p k q k ═ ∞
n= 1 k = 1
Исследуем схожесть этого ряда. Проведем выделение ассимптотики главного члена.
( 2 n ) ! ( 2 n ) !
Cαn
n
=
n
! n !
=>
общее член Рi
i ( n
) – n
! n
! pⁿ
q
ⁿ
Воспользуемся формулой Стирлинга ( при n → ∞ )
n
! ~ √ 2 π n
n n
e -n
(главный член асимптотики) ─ определяет
сходимость ряда.
(
2 n
) ! √ 2 n 2 π
(2 n) ² ⁿ e
-2
n 4n
C
an
n
=
n
! n !
˜ 2 π n n 2
n
e - 2
n =
√ π n
4ⁿ ρⁿ qⁿ ( 4 ρ q
)ⁿ
Итак
,
Рi
i
( n ) √ 2 π n
√ 2 π n
Значит ряд исходный расходится, если расходится ряд
∑ ( 4
ρ
q
)ⁿ
n= 1 √ 2 π n
Следовательно, нужно проверить сходимость и расходимость этого ряда
1) Если ρ = q = 1 / 2, то 4 ρ q = 1
n= 1
√ 2
n 
n= 1
√ 2
n
т.о. i - возвратно.
≥
2
ρ
q ; 1
/ 2 ≥ √ ρ
q
,
ρ q ≤ 1 / 4, 4 ρ q = γ < 1, причем ρ ≠ q , то 4 ρ q = γ < 1
∑ ( 4 ρ
q
)ⁿ =
∑ γ
ⁿ =
следовательно, i
- невозвратно.
n= 1
√
n 
n= 1
√
n
Вывод. В симметричном случае ρ = q = 1 / 2 все состояния возвратны, в
несимметричном случае все состояния невозвратны.
Прокомментируем с точки зрения глобального поведения марковской цепи:
Как известно, в конечное состояние процесс может возвращаться с
вероятностью 1 конечное число раз (эту теорему мы доказывали выше).
Конечное число возвращений связано с тем, что процесс будет переходить (преимущественно) в ту сторону, где вероятность перехода за 1 шаг больше. Через конечное число шагов с вероятностью 1 уже никогда не вернется в исходное состояние i . Т.о. глобально имеется снос процесса (дрейф) либо b + ∞, либо b – ∞, в зависимости от того какой из параметров
больше. ────┬────────────►+
∞
ρ > q
Напротив, если же ρ = q, то процесс не сносит в ∞, он эволюционирует
Бесконечно долго, возвращаясь бесконечно много раз в исходное состояние.
4
.
Положительность.
В несимметричном случае ρ ≠ q все состояния невозвратны, а следовательно нулевые.
В
симметричном случае ρ = q дело обстоит
сложнее и состояния будут возвратны,
но нулевые ( обоснование будет после
асимптотических свойств для вероятностей
перехода Р i i ( n )
).
Комментарий ко всем 4-м свойствам:
-
Х – множество состояний существенных и невозвратных ( класс бесконечный ).
-
Х – класс возвратных и нулевых состояний ( бесконечный ).
-
Многомерное случайное блуждание.
Будем рассматривать только симметричный случай.
Х = { ( a 1,
… a m
), a ¡
,
i = 1,
m ( целые ) }, m ≥ 1.
(1) (m)
n = ( n , …, ) - многомерный случайный вектор.
(1) (1) (m) (m)
n + 1 = ( n + a n , …, + a n ) – случайное смещение на n + 1,
(1) (m)
где ( a n , …, a n ) = ( i 1, i 2 , …, i m ) с вероятностью 1 / 2 m , i k = ± 1, k = 1, …, m.
Этих двумерных векторов будет 2 m .
Например, при m = 2. Пусть n = ( a 1 , a 2 )
Двоичные векторы ( i 1, i 2 ) :
(
a1-1,
a2+1)
(a1+1,
2-1)
( 1, -1 ), ( -1, 1 ), ( -1, -1 ); 2 m
= 2 2
= 4
|
|
|
|
(1) ( 2) ( 1, 1 ) с вероятностью¼ (a n, a n ) ( 1, -1 ) с вероятностью ¼ ( -1, 1 ) с вероятностью ¼ ( -1, -1 ) с вероятностью ¼ Это наши добавки |
|
|
|
|
(a1, a2) |
|
|
(a1-1, a2-1) (a1+ 1, a 2-1)
Получим двумерное симметричное блуждание.
Исследуем вероятность:
Итак, по условию, если n = ( a 1, a 2, …, a m )
P ( n + 1 = ( a 1 + i 1 , …, a m + i m ) | ( a 1 , …, a m ) ) = 1 / 2 m ( 1 )
m ≥ 1
Рассмотрим одномерное блуждание { ( k ) } по k- ой координате.
(k) (k)
P ( n + 1 = a k + i k | n = a k ) = ½, i k = ± 1, k = 1, 2 , … , m.
m (k)
Тогда П Ρ ( n + 1 = a k + i k | n = a k ) = 1 / 2 m ( 2 )
n= 1
С
P ( n + 1 = ( a 1 + i 1 , …, a m + i m ) | n = ( a 1 , …, a m ) ) =
(1) (m) (1) (m)
P ( n + 1 = ( a 1 + i 1 , …, n + 1 = a m + i m | n = a 1 , …, n = a m ) =
m (k) (k)
П Ρ ( n + 1 = a k + i k | n = a k ) = 1 / 2 m ( формальное приравнивание ).
k= 1
Обозначим его ( 3 ).
Из ( 3 ) следует блуждание по каждой координате , независимые случайные величины (совместная вероятность равна произведению вероятностей).
Лекция № 10
(k)
{ n , k = 1, 2 , … , m } – независимы.
Т.к. эти величины независимы, то вероятность будет представлять вероятность многомерного блуждания, равного произведению вероятностей одномерных блужданий:
(1) ( 2 ) (m ) ( 1 ) ( 2 ) (m )
Pa, a (2k) = P ( 2 n = a 1, 2n = a 2 , …, 2n = a m | 0 = a 1, 0 = a 2 ,…, 0 = a m) =
m (k) (k)
= П Ρ ( 2n = a k | 0 = a k )
k= 1
a = ( a 1, …, m )
Для одномерного случая блуждания:
(k) ( k ) 1
P
a
k
,a k
(2n) = P (
2 n = a k
|
0 = a k
) ~ , n → ∞
( 1 )
√ 2
a
Тогда многомерное случайное блуждание возвращается ↔
m
n= 1
√
n
Ряд ( 2 ) расходится ↔ m = 1, 2 , … , сходится при m ≥ 3.
Вывод. Симметричное случайное блуждание возвратно при m = 1, 2 , … и невозвратно при m ≥ 3.
4. Периодичность.
Зафиксируем начальное 0 = i X. Рассмотрим последовательность целых
чисел n 1 n 2 n 3 … таких, что Р i i ( n k) 0, k = 1, 2 , … {n k} – длины циклов
Введем параметр
d = d ( i
) = ΗΟD { n 1,
n 2 , … ) - наибольший
общий делитель всех длин циклов.
n k Рассмотрим два случая:
шагов 1) если d = 1, то составляющая i - непериодична
i
2) если d
> 1, то составляющая i
- периодична с периодом d.
В этом (2) случае все длины циклов будут кратны периодам, т.е. n k = k d, k = 1, 2 , …
d - минимальное число шагов, за которое можно будет вернуться из состояния i в себя.
Из определения периодичности => , что справедливо следующее:
Р i i ( k d ) > 0, k = 1, 2 , …, Р i i ( s ) = 0, s ≠ k d, k = 1, 2 , …
Теорема. (альтернатива солидарности)
В одном классе все состояния либо периодичны, либо непериодичны, период у них одинаковый.
Иначе: Если і‚ ј C, C – класс ( i ~ j ), то
d ( i ) = d ( j ).
Доказательство. Пусть i ~ j ( сообщающиеся ). Тогда такие два числа m, n > 0 (число шагов), что
Р j i ( m ) = α > 0; Р j i ( n ) = β > 0.
В силу предыдущих оценок имеют место следующие оценки:
Р i i ( k + m + n ) ≥ Р i ј ( m ) Р j ј ( k ) Р ј i ( n ) = α β Р j ј ( k ), k ≥ 1 ( 1 )
Р i i ( m + n ) ≥ Р i ј ( m ) Р ј i ( n ) = α β > 0 ( 2 )
Пусть i - периодичность с периодом d ( i ) = d ;
j - составляющая, для которой определен параметр d ( j ).
Тогда, если i - периодична => , что из ( 2 ) по определению => m + n кратно d.
Тогда рассмотрим в соотношении ( 1 ) левую часть:
если k - некратно d, то k + m + n - некратно d => левая часть ( 1 ) = 0, т.е.
Р i i ( k + m + n ) = 0, k ≠ s d => из ( 1 ) Р j ј ( k ) = 0, k ≠ s d.
Значит Р j ј ( k ) > 0, только при тех значениях “ k” , для которых “k” кратно “d “.
Отсюда следует, что d ( j ) ≥ d = d ( i ).
───┬───┬───┬───┬────►
0 d 2d ℓd
↑ ↑ ↑ ↑
Р j ј ( k ) > 0 только в этих точках
Меняя местами i и j из соотношения ( 1 ) и ( 2 ) получаем оценки, которые могут быть доказаны аналогично:
d ( i ) ≥ d (j ) => d ( i ) = d ( j ) => эти два параметра равны => эти
периоды равны.
Пусть С – периодичный класс, d - период С
( d = d ( i ), і C ).
Теорема. Любой периодичный класс представляется в виде объединения
подмножеств (непересекающихся), которые называются циклическими
подклассами класса С.
C = C ( 0 ) C (1) … C ( d - 1) , C ( r ) ∩ C ( s ) = , r ≠ s
{ C ( k ) , k = 0, 1, …, d – 1 } - циклические подклассы.
Доказательство. Пусть 0 = i С фиксированное состояние нашего класса. Введем следующие множества:
C ( 0 ) = { j С : Р i j ( k d ) > 0, k = 1, 2 , …} i С ( 0 )
C ( 1 ) = { j С : Р i j ( 1 + k d ) > 0, k = 0, 1 , …}
C ( ℓ ) = { j С : Р i j ( ℓ + k d ) > 0, k = 0, 1 , …}
C ( d - 1 ) = { j С : Р i j ( d – 1 k d ) > 0, k = 0, 1 , …}
Т.о. мы ввели d подмножеств множества С. Объединение этих подмножеств составляет весь класс С.
C ( 0 ) C (1) C (2) … C ( d - 1) = C
Действительно, в определении рассмотрены все варианты
m = ( ℓ + k d ), ℓ = 0, 1 , … d – 1. Р j i ( m ) > 0.
Других множеств, т.е. других состояний нет.
Докажем, что они не пересекаются:
C ( r ) ∩ C ( s ) = , r ≠ s
Пусть для определенности 0 ≤ ґ < ѕ ≤ d – 1. Пусть они пересекаются. Действие от противного. Т. е пусть 0 = i C ( r ) ∩ C ( s ). Тогда по определению подклассов:
Р i , j 0 ( r ) > 0, Р i , j 0 ( s ) > 0.
Но тогда можно из j o вернуться в i за оставшееся число шагов:
Р i , j 0 ( d – r ) > 0, Р i , j 0 ( d – s ) > 0.
) r
(
C
i
Возьмем и объединим две ветви r и d – s =
Р i i ( r + ( d – s ) ) ≥ Р i , j 0 ( r ) Р j 0 , j ( d – s ) > 0.
Но r + (d – s) < d - это противоречие,т.к. должно быть кратно d = C ( r ) ∩ C ( s ) = , r ≠ s
По построению очевидно:
C ( 0 ) → C (1) → … → C ( d - 1) → C ( 0 ) (циклические),
Переход осуществляется по циклу, перейти из одного процесса в другой можно только за d шагов.
Лекция № 11
Пусть d период класса С, d > 1. Разбили С на d циклических подклассов
С = C ( 0 ) C (1) … C ( d - 1). Переходы в этом классе происходят по циклу.
Отметим, что: пусть заданы два подкласса C ( r ) и C ( r + ), 0 ≤ ґ < r + = d – 1. Тогда переходы из состояния в состояния происходят так:
положительное, если
m =
+ nd,
n = 0, 1…
Р i j (m)
ноль, если m ≠ + nd, n = 0, 1…
i С ( r ) , j С ( r + )
Поглощающие цепи Маркова
Определение. Марковская цепь { n } c множеством состояний Х называется
поглощающей, если у нее все замкнутые классы состоят каждый из одного состояния (т.е. состояния поглощающиеся), а все остальные состояния образуют незамкнутый несущественный класс.
1
А
В, А -
несущественный ( незамкнутый) класс;
B – { 1,
2, … k } – поглощающие
А { k
+ 1, k
+ 2, … k
+ r
}
М
атрица
вероятностей перехода ( МВП ) имеет
следующую структуру (поглощающие
марковские цепи):
где I
= 1 0 размера k
x k, переходы
В
В;
I
O 0 1
P
=
R Q О = 0.
. 0 - нулевая,
размера k x
r, соответствует
-
0
переходам В А (невозможен);
R
= Р i j размера
r x k,
переходам за 1 шаг А
В (поглощение);
Q = Р i j размера r x r, переходы внутри А : А А.
Поглощающая марковская цепь ведет себя следующим образом:
на конечном шаге с вероятностью 1 процесс (цепь) выходит из множества А и
и поглощается в состоянии множества В. Так завершается реализация процесса.
Примеры.
-
Демографические модели.
Анализ перехода одной группы лиц в другую является применением этой модели.
Поскольку поглощения связаны, например, с выбытием гражданина из определенного региона и он перестает учитываться. Модель с поглощающим состоянием отвечает жизни. Это - одна из важнейших моделей.
2) Они связаны с анализом финансового состояния той или иной структуры (счет в
банке). Поглощение – это состояние, которое отвечает, либо банкротству, либо
иное состояние, в котором нельзя продолжить деятельность.
Некоторые вспомогательные материалы из
теории матриц.
Определение.
Пусть W – матрица, W = (W i j , i, j = 1, 2 , … , n )
W ( n ) = (W i j ( n ) ), n = 1, 2 , … - последовательность матриц.
Будем говорить, что матрица W ( n ) сходится к W, если имеет место сходимость по каждому элементу:
W ( n ) W i j , i, j = 1, … , r.
n→ ∞
Теорема. Пусть W = (W i j , i, j = 1, … , r ) – квадратная матрица, и ее n- ая степень 0: W n О, n → ∞. Тогда обратная матрица ( I – W ) –1, причем
( I – W ) –1 = I + W + W 2 + … = ∑ W n, где I – единичная матрица.
n >0
Доказательство. Заметим, что можно написать следующее соотношение:
( I
– W )
( I
+ W + …+
W n
– 1
) = I
– W n,
( 1 )
Заметим также: I – W n → I при n → ∞ ( по условиям W n 0 ).
Но отсюда: det ( I – W n ) → 1 при n → ∞ (т.к. есть сходимость матриц
=> есть сходимость определителей этих матриц).
Последнее свойство означает, что n 0 1: при n n 0 имеет место
det ( I – W n ) 0 (положительное число).
Применим операцию определитель к ( 1 ).
det [ ( I – W ) ( I + W + …+ W n – 1 ) ] = det [ I – N n ]
Определитель произведения равен произведению определителей:
det ( I – W ) det ( I + W + …+ W n – 1 ) = det ( I – N n ) 0, n n 0
=> слева два сомножителя, ни один из них не равен 0 => det ( I – W ) 0
=> обратная матрица ( I – W ) – 1
Умножим обе части ( 1 ) на ( I – W ) – 1 слева:
( I
– W )
– 1 ( I
– W )
( I
+ W + n
1
+ W
n –
1
) = ( I
– W )
– 1 ( I
– W n
)
единичная матрица
При переходе к пределу матрица справа будет стремиться к ( I – W ) – 1 :
lim ( I –W ) – 1 ( I –W n ) = ( I –W ) – 1 = lim ( I +W + …W n – 1 ) = ∑ W k
n→ ∞ n→ ∞ k >0
(этот бесконечный ряд выражает обратная матрица).
Возвращаемся к марковским цепям . Обозначим Ni j – число попаданий марковской цепи в j A до поглощения при условии 0 = i А.
М N i j = m i j , i, j = 1, … , r . M ( m i j , i, j = 1, … , r ) – матрица математических ожиданий, при условии, что начальное состояние равно i.
Введем N i = ∑ N i j - суммарное время до поглощения, при 0 = i.
jА
m i = М N i = ∑ M N i j - среднее математическое ожидание времени до поглощения .
jА
Пусть однократное попадание в состояние j составляет доход c j. Тогда S i = ∑ c j N i j
jА
-
случайный
доход до поглощения при
0 = i.
М S i
= ∑ c j
m i j
- математическое ожидание
дохода до поглощения.
jА
Л
емма.
Пусть 1,
если
n
= k
I i j ( n = k) =
0, если n ≠ k ( индикатор)
Тогда М ( I ( n = j ) ( 0 = i ) = Р i j ( n ).
М ( I ( n = j ) I ( m = k ) | 0 = i ) = Р i k ( m ) Р n j ( n - m ), n m.
Лекция № 12
Доказательство. Возьмем событие ( не только индикаторное, из нашей сигма алгебры А ) событие S А.
М ( I ( n = j | 0 = i ) = Р ( n = j | 0 = i ) = Р i j ( n ).
Заметим , что кроме того
I ( n = j ) I ( m = k ) = I ( n = j , m = k )
Произведение индикаторов равно индикатору произведений.
Тогда:
М ( I ( n = j ) I ( m = k ) | 0 = i ) = M ( I ( n = j , m = k ) | 0 = i ) =
P ( n = j , m = k | 0 = i ) = Р i k ( m ) Р k j ( n - m ), ( 0 ≤ m < n ) .
Теорема. Для поглощающей цепи Маркова { n } в веденных обозначениях имеет место матричная формула:
М = m i j = ( I – Q ) – 1
I – единичная матрица ( r x r )
Q – матрица А → А (несущественная)
Доказательство. При условии фиксированного начального состояния 0 = i А,
мы можем записать число, которое нас интересует:
( 1 ) N i j ∑ I ( n = j ) – общее число попаданий в состояние j до поглощения.
n >0
Замечание. при n = 0 (начальные состояния i и j совпадают)
1,
i
= j
- будем считать так, если n
= 0
I ( 0 = j ) = δ i j =
0, i ≠ j
В ( 1 ) возьмем математическое ожидание от обеих частей:
m i j = М N i j = ∑ М ( I ( n = j ) | 0 = i ) = { по лемме } =
δ i j + ∑ Р i j ( n ) , i, j А можно считать от 1 до r ( 2 )
n = 1
Соотношение ( 2 ) можно переписать в матричном виде:
М ≠ I + Q + Q 2 + … ≠ ∑ Q n
n > 0
Поскольку Q n → 0 n → ∞ , т. е цепь на конечном шаге выйдет из множества состояний А, т.е. Р i j → 0.
По теории о матрицах:
М = ∑ Q n = ( I – Q ) – 1
n > 0
Зафиксируем начальное состояние 0 = i А и j состояние из В – поглощающее.
Введем вероятность b i j – вероятность того, что поглощение в j при условии 0 = i
(например, демография: смерть, переезд в другой регион или не учитываемую группу лиц; это выход из цепи по какой-то причине, но связанной с j ; экономика: банкротство и т.п.).
j характеризует причину остановки или поглощения процесса.
Исследуем этот момент.
Создадим матрицу: В = ( b i j ), i А, j В.
Т
еорема.
Для матрицы В имеет место формула:
В = М R =
( I – Q
) – 1 R ,
где R – одна из
клеток матрицы вероятных переходов.
Н
апоминание:
I
O
P
= R
Q
Доказательство. Воспользуемся Марковским свойством, и по свойству классической вероятности можно записать:
( 1 ) b i j = Р i j + ∑ Р i ℓ b ℓ j , i А, j В (либо переход из i в j ,
ℓА
либо в
промежуточное состояние ℓ внутри А)
Перепишем состояние ( 1 ) в матричной форме:
В = R + Q B
В – Q B = R
( I – Q ) B = R - также произведение, т.к матрица некомутативна.
Знаем, что обратная матрица, то
В = ( I – Q ) – 1 R
Пример применения этой теоремы – задача № 2 из контрольной работы № 1.
Цепи Маркова. Предельные и стационарные распределения.
! Изучает поведение цепи при длительной эволюции (связано с контр. работой № 2).
Позволяет изучать стабильные системы.
Изучает стабильные установившиеся режимы и их характеристики.
Определения:
-
Если для марковских цепей { n } существуют пределы вероятности перехода
lim Р i j ( n ) = j , не зависящие от начального i , и причем вектор таких пределов
n→ ∞
образует распределение вероятностей:
Π = ( j , j Х ) – образует распределение ( j ≥ 0, j Х, ∑ j = 1 ),
j х
то данный вектор Π = ( j , j Х ) называется предельным распределением марковской цепи.
2. Предельное распределение называется эргодическим, если все его компоненты строго положительны j > 0, j Х. В этом случае сама цепь Маркова тоже называется эргодической цепью Маркова.
3. Распределение вероятностей (это вектор со свойствами, характеризующий дискретную случайную величину) Q = ( q j , j Х ) ( т.е. q i ≥ 0, i Х, ∑ q i = 1 )
i х
называется стационарным или инвариантным распределением для марковской цепи { n }, если удовлетворяются следующие соотношения: q j = ∑ q i Р i j, j Х ( 1 )
i х
Вид соотношения ( 1 ) в матричном виде: Q = Q P, Q инвариантно относительно преобразования, задаваемого матрицей Р ; если j - six, то вектор q j умножаем на первый столбец матрицы Р и т.д. в результате получаем вектор.
Замечание. Если стационарное распределение и единственно, то оно будет представлять собой единственное решение системы уравнений ( 1 ).
4.
Цепь Маркова {
n
} называется
стационарной
Марковской цепью,
если для
ℓ ≥ 0 совместное распределение вида:
Р (
k
=
i 0
,
k+1
=
i1 ,
… ,
k+ℓ =
i ℓ
) при
состояниях i : i 0
, i1
, … , i ℓ
Х не зависит от k
( k
≥ 0 )
от сдвига начального времени не зависит – это стационарность: сдвиг по времени длины ℓ + 1.
Примечание. Введенное определение относится к более широкому классу процессов, чем цепи Маркова. Процессы удовлетворяющие этому свойству называются стационарными в узком смысле. Подобное определение можно применить и к непрерывному времени.
Эти свойства требуют анализа.
Замечание. Связь свойства стационарности марковской цепи со стационарным
распределением ( первый аналитический вопрос)
Заметим, если начальное распределение марковской цепи совпадает со стационарным: P { 0 = i } = q i , i Х, т.е. P 0 = Q (векторная формула)
P ( 0 ) = ( P i ( 0 ) = P { 0 = i }, i Х ) – это вектор – начальное распределение.
Если это выполнено, то можно доказать, что n ≥ 1
P ( n ) = ( P i ( n ) = P { n = i }, i Х ) = Q имеет место это свойство, затем (после совпадения) не меняется и остается стационарным.
Проверим это:
Действительно ( для n – шага):
P i j ( n ) = P ( n = j ) = { по формуле полной вероятности} =
= ∑ P ( 0 = i ) P ( n = j | 0 = i ) = ∑ P i ( 0 ) P i j ( n ) дляn ≥ 1 , целого.
i х i х
В векторной (матричной) форме:
( 1 ) P ( n ) = P ( 0 ) P n
C другой стороны, по определению стационарного распределения (инвариантного):
Q = Q P = { можно применять это свойство сколько надо раз } =
= ( Q P ) P = Q P 2 = … = Q P n , n ≥ 1 ( 2 )
( менять местами нельзя, а ассоциативность есть)
Если ( 1 ) вместо P ( 0 ) поставить Q : P ( 0 ) = Q , то
P ( n ) = Q P n ( 3 )
Сравнивая ( 2 ) и ( 3 ) получаем, что из ( 2 ) и ( 3 ) следует
P ( n ) = Q.
Начальное распределение совпадает со стационарным, следовательно и вся цепь стационарна.
Действительно: чтобы это проверить рассмотрим совместное распределение:
( 4 ) Р ( k = i 0 , k+1 = i1 , … , k+ℓ = i ℓ ) = { запишем по формуле условной вероятности } =
= Р { k+1 = i1 , k + 2 = i 2 , … , k+ℓ = i ℓ ) | k = i 0 ) Р ( k = i 0 )
Заметим, что если начальное совпадает со стационарным распределением, то
P ( 0 ) = Q , то Р ( k = i 0 ) = q i o
C другой стороны
( 5 ) Р ( k+1 = i1 , k + 2 = i 2 , … , k+ℓ = i ℓ ) / k = i 0 ) =
= Р ( k+1 = i1 | k = i 0 ) Р ( k + 2 = i 2 | k+1 = i1 ) … Р ( k + ℓ = i ℓ ) | k+ ℓ - 1 = i ℓ - 1 )
= ( в силу однородности не зависит от k , а от номеров состояний зависит ) =
= Р i 0, i 1 Р i 1, i 2 … Р i ℓ - 1, i ℓ ( 6 )
Из ( 5 ) и ( 6 ) => в ( 4 ) правая часть не зависит от k { n } – стационарная марковская цепь.
Лекция№ 13 Эргодическая теорема для переходных вероятностей.
Пусть задана марковская цепь { n }. Ее вероятность перехода за n шагов
Р ( n ) = ( Pi j ( n ) ) i, j Х;
Рассмотрим следующие случаи:
-
Пусть j Х – фиксированное состояние, j – возвратно ( μ J = 1 ) и не периодично
( d ( j ) = 1 ). Тогда, если i сообщается с j ( i ~ j ) , то lim Р i j ( n ) = 1 / μ j .
n→ ∞
μ j = М ( υ n - υ n – 1 ) М - обращение времени между последним обращением в υ j.
В частности, если состояние j положительно ( т.е. μ j < ∞ ), то 1 / μ j > 0; если j - нулевое состояние ( μ j = ∞ ), то 1 / μ j = 0.
2. Пусть j – возвратно, ( d ( j ) = 1 ), i = j ( j достижимо из i )
Тогда V ( i j )
lim Р
i j (
n ) =
μ
j
n→ ∞
V ( i , j ) = ∑ V n ( i j ) = ∑ P ( 1 ≠ j , 2 ≠ j … , n-1 ≠ j, n = j | 0 = i ).
n = 1 n = 1
3. Пусть j – возвратно, с периодом d ( j ) > 1 , i ~ j (принадлежат одному классу. Рассмотрим такой случай:
d
lim Р
i j (
a +
nd ) =
μ
j
n→ ∞
4. Пусть j – возвратно, может быть периодично , i и j могут принадлежать к разным классам, i → j . Тогда
lim Р i j ( a + nd ) = [ ∑ Рa + r d ( i, j ) ] , a = 0, 1, …, d - 1
n→ ∞ r = 0
d = d ( j )
Примечание к пункту 3.
Если s ≠ a + nd, то lim Р i j ( s ) = 0
s → ∞
Если рассм. произв. посл. m, то lim Р i j ( m ) не существенно.
m → ∞
Теорема. Пусть { n } - марковская цепь. Р ( n ) = ( Pi j ( n ) ) i, j Х.
Пусть j Х – невозвратное состояние, или возвратное нулевое, j Х -
произв.
Тогда lim Р i j ( n ) = 0
Альтернатива солидарности для свойства положительности
Пусть в марковской цепи i ~ j ( i, j С – класс). Тогда они оба либо положительные, либо нулевые.
Доказательство. ( в простейшем случае). Наш класс С не периодичный. Тогда, т.к. i ~ j, то целые числа k, ℓ такие, что Р i j ( ) > 0, Р j i ( ) > 0.
Рассмотрим неравенство Р i j ( n + k + ℓ ) ≥ Р i j ( k ) Р j j ( n ) Р j i ( ℓ ) ( 1 )
Предположим, что состояние j – положительно ( следовательно возвратное и не периодичное ). Тогда можно взять предел от обеих частей нашего неравенства ( 1 ), запишем при этом
lim Р j
j (
n ) =
> 0 (эргодическая теорема)
n→ ∞
lim Р i i ( n + k + ℓ ) ≥ Р i j ( k ) Р j i ( ℓ ) lim Р j j ( n ) =
n→ ∞
n→ ∞
= Р i j ( k ) Р j i ( ℓ ) > 0
Отсюда следует, что lim Р i i ( m ) = > 0 , i – положительное.
m → ∞
Аналогично, меняя местами i и j , получаем , что если состояние i – положительное,
то и состояние j – положительное.
Итак, это утверждение доказано, когда С – непереодичный класс, i , j – положительны одновременно.
Самостоятельно доказать это утверждение, когда С – периодичный класс.
Теорема. Пусть марковская цепь { n } неприводима и множество состояний Х ее –
конечно.
Тогда имеет место следующее
утверждение
неприводимая
неприводимая { 1 } возвратная { 2 }
непериодическая <=═> положительная <=═> ( эргодическая )
непериодическая
Д
оказательство.
1. неприводимая
возвратная
непериодическая =═> положительная
в конечном случае.
От противного. Пусть все состояния цепи невозвратны
(альтернатива солидарности). Запишем условия нормировки:
∑ P i j ( n ) = 1 , n ≥ 1 , i Х – произвольно.
i х
Перейдем к пределу при n→ ∞:
1 = ∑ P i j ( n ) = ∑ lim Р j j ( n ) = 0 ( т.к., по теории после эргодической )
n→ ∞ j = 1
Получили противоречие. Итак, все состояния возвратны.
Если j 0 Х – возвратное нулевое, то все состояния возвратные нулевые.
Аналогично приходим к противоречию =═> все состояния будут возвратными и положительными.
Замечание. Мы это делали в простейшем случае. Всякий конечный замкнутый класс
будет возвратным и положительным.
Теперь доказана эквивалентность { 1 }.
Осталось проверить { 2 }.
Пусть
неприводимая
непериодическая выполнены.
положительна
возвратная
Тогда lim Р i j ( n ) = j = > 0 ; i, j Х – произв., фиксированные
n→ ∞
(смотри пункт 1 в эргодической теореме)
конеч. Х
∑ j = ∑ lim P i j ( n ) ======= lim ∑ P i j ( n ) = 1
j х j = х n→ ∞ n→ ∞ j х
Итак, = ( 1, 2, … , r ) – образуют эргодическое распределение.
Лекция № 14
Теорема. Пусть { n } марковская цепь. Х = { 0, 1, …, r } – конечно,
P ( n ) = (P i j ( n ), i, j Х ). Тогда справедливы соотношения
неприводимость
неприводимость возвратность
не периодичность <=═> положительность <=═> ( эргодическая )
не периодичность
Доказательство. Докажем, что, если марковская цепь эргодическая, то она
неприводимая и не периодичная (все остальное приложится).
В силу эргодичности существует
lim P i j ( n ) = j > 0 , j Х и ∑ j = 1 ( i, j Х )
n→ ∞ j х
(начиная с некоторого номера так будет непрерывно). Тогда 0 (окрестность) такое, что j > 0 и n i j такое, что Р i j ( n ) ( j - , j + ), n n i j =═>
=═> Р i j ( n ) > 0 при n n i j ,
т.е. все состояния сообщаются (неприводимость).
Далее, если i = j , то номер n i > 0, такой, что P i i ( n ) > 0 при n n i j (т.е. периодичности быть не может).
Если
состояние i – периодичное,
то P i
i
( k d
) > 0, k = 1,
r. Это противоречит
предыдущему утверждению, т.е. периодичности
нет, т.е. состояние i – не
периодическое, а это значит, что все
остальные состояния – не периодические.
Марковские цепи со счетным множеством состояний
Теорема. (о необходимых условиях существования пределов вероятности перехода)
Пусть { n } марковская цепь. Х = { 0, 1, …, r } – счетное,
матрицы вероятностей перехода
P ( n ) = (P i j ( n ), i, j Х ).
Предположим, что i, j Х существует предел
lim P i j ( n ) = j , не зависящие от i Х
n→ ∞
Тогда имеет место утверждение:
1.) ∑ j ≤ 1 и j = ∑ i p i j , j Х
j х i х
2.) Альтернатива: либо j > 0, j Х , либо ∑ j = 1
j х
3.) Если j > 0, j Х , то не существует ни предельного, ни стационарного
распределений.
Если ∑ j = 1, то = ( j, j Х ) – вектор пределов, образующий единственное
j х
стационарное распределение.
Без доказательства.
Следствие (из теоремы):
Если в марковской цепи существует предельное распределение, то оно же
и является единственным стационарным распределением.
Замечание.
1. Свойство j = ∑ i p i j , j Х выполняется всегда. Оба случая
i х
рассмотренные в 2.) полностью описывают поведение системы, это справедливо и
для более общих случаев (например, марковские процессы с непрерывным
временем). Помимо чисто фундаментального смысла теоремы, данная теорема
имеет важное значение как вспомогательный результат, который дальше
используется в доказательствах дальнейших утверждений ( относительно
предельных и стационарных распределений).
Без доказательства.
Теорема. (необходимые и достаточные условия существования и единственности
единств по стационарности распределения):
Единственное стационарное распределение марковской цепи тогда и
только тогда, когда в марковской цепи найдется ровно один возвратный
положительный класс.
Без доказательства.
Приведем следующие дополнения (пояснения)
Пусть N – число возвратных положительных классов данной марковской цепи { n }.
Тогда имеет место утверждение:
Е
сли
N = 0, то у марковской цепи
стационарное распределение.
Если N = 1, то единственный положительный возвратный класс, то единственное стационарное распределение.
Если N ≥ 2, то множество (бесконечно много) стационарных распределений.
-
Пусть N = 1, С - единственный положительный возвратный класс,
Положим 1 / μ j
, j C
q =
0,
j
C
Тогда Q = ( q j , j Х ) и образует единственное стационарное распределение.
Это утверждение верно вне зависимости от того является ли С периодичным или не периодичным.
Т.о. нашли стационарное распределение как решение системы, а μ j определяем из условия q j = 1 / μ j .
Система
q j = ∑ q i p
i j , j Х
i х
∑ q i = 1
i х
1 / q j , j C
μ j =
∞ ,
j
C
Теорема. (о необходимых и достаточных условиях существования предельного
распределения)
Предельное распределение марковской цепи тогда и только тогда, когда в
марковской цепи найдется ровно один возвратный не периодичный класс С,
причем для состояний i Х, j C вероятность перехода за
конечное число шагов V ( i, j ) = 1.
V ( i, j ) = ∑ V n ( i j ) = ∑ P ( 1 ≠ j , 2 ≠ j … , n-1 ≠ j, n = j | 0 = i ).
n = 1 n = 1
Лекция № 15
Замечание.
-
Если Х – конечно, то V ( i, j ) = 1.
В цепях Маркова: С – единственно возвратный положительный не
периодический
-
возвратный положительный периодический
-
возвратный нулевой
-
невозвратный
Если
возвратный, положительный, периодический,
то
и другой возвратный, положительный,
периодический =═>
единственное стационарное распределение
=
═>
нет и предельного распределения =═>
возвратный положительный периодический
класс.
-
в
озвратный
нулевой класс в конечной цепи.
-
Связь условия существования предельных и единственных стационарных
распределений
предельное распределение стационарное распределение
● i
i
возвратность возвратность
положительность
положительность
не
периодичность V i
j =
j
V i
j >
1
Теорема. Для конечной марковской цепи имеет место следующее соотношение
неприводимость
возвратность
( эргодическая ) <=======═> положительность
(
4 ) ( 1 ) не
периодичность
(
предельное
распределение )
( 6 )
( 2 )
( ! возвратный
положительный
( 5 ) непериодический класс )
( 7 )
(
! стационарное
распределение ) (
! возвратный положительный класс)
( 3 )
Доказательство.
( 4 ) по определению эргодического распределения
( 5 ) по следствию из теоремы о необходимости условий существования предельных
вероятностей перехода.
( 6 ) очевидно
( 7 ) очевидно
( 1 ) теорема о конечной эргодической марковской цепи
( 2 ) теорема о предельного распределения и замечания к ней
( 3 ) теорема о единственного стационарного распределения
Функционалы от марковской цепи (аддитивные)
{ n } - однородная марковская цепь.
P ( n ) = (P i j ( n ), i, j Х ).
Х = { 0, 1, … } – дискрет (счет)
С: Х → R ; С ( i ) = с i – доход при одном попадании в i.
n
Определение. Семейство { η n n ≥ 0 }, η n = ∑ C ( k ).
аддитивный функционал k = 0
Эргодическая теорема для аддитивного функционала дохода
Пусть { n } – неприводимая, возвратная и положительная, функция с i , i Х
∑ | C ( і ) | π і < ∞, где Π = ( π і ј ) - стационарное распределение
i х
Тогда справедливо:
1. начального i Х
n
Р ( lim ∑ C ( k ) = ∑ C j π ј | 0 = i ) = 1
n→ ∞ k = o i х
2. начального i Х
n
lim M { | ∑ C ( k ) = ∑ C j π ј | 0 = i } = 0
n→ ∞ k = o i х
Без доказательства.
Лекция № 1. Ветвящиеся процессы с дискретным временем
Примеры моделей ветвящихся процессов
-
Нейтронная ядерная (цепная реакция)
ч
астица
(нейрон)
0 
0 = 1 – одна начальная частица
на следующем этапе – их уже некоторое число 1, на втором шаге - 2.
Процесс за конечное время может либо затухнуть ( не будет ударов), либо вызвать взрыв (очень много ударов).
-
Выживание фамилий
Передача идет только по мужской линии - 1 – число сыновей в первом шаге
(число потомков) 1, 2 - общее число потомков от одного основателя. 0 –
основатель (их может быть несколько, например, братья).
0
(основатель)
сыновья внуки
Особенности общей модели
-
Две частицы порождают потомков независимо от всех других частиц.
-
Вероятности, с которыми частицы порождают потомков, одинаковы.
Эти предположения положены в основу
ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Введем такие объекты:
i ( n ) – система случайных величин (количество потомков, порождаемый i – й частицей в n – м поколении), n = 0, 1, 2, …
Будем предполагать, что случайные величины { i ( n ) } – независимы и одинаково распределены.
Зададим распределение:
Р ( i ( n ) = k ) = p k , p k – задает распределение вероятности, k = 0, 1, 2, …
∑ p k = 1, n ≥ 1.
k = 0
Определение. Ветвящимся случайным процессом с дискретным временем будем называть последовательность случайных величин, заданную соотношением:
η i
η n + 1 = ∑ i ( n ) , n = 0, 1, 2, …
i = 1
η 0 - начальное фиксированное значение (этта). η 0 = i 0 ≥ 1.
Иллюстрация:
η 0
1
(
0
)
η 1
= ∑
i
(
0
)
i = 1
2
(
0
)
η 1
= ξ 1
( 0 )
Итак, это есть марковский процесс. Имеется также независимость от прошлого, если η нач. фиксируем, то η n +1 - сумма независимых величин.
Запишем следующее:
Условная вероятность:
η n + 1 = j | η n = i = Р ( ξ 1 ( n ) + ξ 2 (n ) + … + i ( n ) = j ) = получили вероятности перехода = суммируем по всем возможным комбинациям =
= ∑ i P k 1 P k 2 … P k i (явное представление)
(
k
1
, k
2
, ... k
i
);
∑ k
s =
j
k
s ≥ 0, s
= 1, i
от n не зависит, значит { η n } – однородная марковская цепь.
Для исследования этих объектов введем производящие функции.
Метод исследования ветвящихся процессов { η n }- метод производящих функций
Введем производную функцию φ ( s ) =∑ Р k S k
k = o
и другая производная функция ( от числа частиц в n –том поколении)
φ n ( s ) = ∑ Р ( η n = k ) S k , n = 0, 1, …
k = o
Если 1 - число потомков от одной частицы Р ( 1 = k ) = p k , k = 0, 1, 2, …
φ ( s ) = М S 1 , φ n ( s ) = М S η n
Замечание:
φ о ( s ) = ∑ Р ( η 0 = k ) S k = S i o
k = o
(вероятность = 1, если неслучайное число частиц; η 0 = i 0 с вероятностью 1 ) –
это производящая функция в начальный момент.
В частности, если η 0 = i 0 = 1 , то
φ 1 ( s ) = ∑ Р ( η 1 = k ) S k = ∑ Р ( 1 = k ) S k = φ ( s )
k = o k = o
П
φ n +1 ( s ) = ∑ Р ( η n +1 = k ) S k = { условную вероятность переписываем через
полную вероятность } ∑ [ ∑ Р ( η n +1 = k | η n = j ) Р ( η n = j ) ] S k =
k = o j = o
= ∑ [ ∑ Р ( ξ 1 + ξ 2 + … + j = k ) Р ( η n = j ) ] S k =
k = o j = o
= ∑ Р ( η n = j ) ∑ P ( ξ 1 + ξ 2 + … + j = k ) Р ( η n = j ) ] S k ( 1 )
j = o k = o
∑ Р ( η n = j ) [ φ ( s ) ] j = φ n (φ ( s ) ) ( 2 )
j = o
Замечание.
Заметим, что если мы напишем математическое ожидание
М S 1 + 2 +…+ j =============== ∑ P ( ξ 1 + ξ 2 + … + j = k ) S k = { в силу
k
= o
независимости } = M ( S ℓ ) M S ℓ = [ φ ( s ) ] j
ℓ = 1 ℓ = 1
подставим в формулу ( 1 )
Лекция № 2
n = 1 в ( 2 ) φ 2 ( s ) = φ 1 ( φ ( s ) )
если φ 1
( s ) = φ ( s ) , то φ 2
( s ) = φ ( φ ( s ) )
если же η 0 = i 0 1 , то φ 1 ( s ) = [ φ ( s ) ] i 0 ( η 0 = 1 )
По индукции можно доказать, что для
k = 0,
n можно записать следующее соотношение
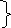φ n
+1
( s ) = φ n
-
k
( φ k
+1
( s ) )
В частности , k = n - 1 φ n +1 ( s ) = φ ( φ n ( s ) ) ( 3 ) η 0 = 1
Соотношение ( 2 ) справедливо при η 0 = i 0 1
Соотношение ( 3 ) справедливо при
Если η 0 = i 0 1 , то вместо ( 3 ) можно получить
φ n +1 ( s ) = φ1 ( φ n ( s ) ) = [ φ ( φ n ( s ) ) ] i 0
Заметим. М η n = φ n ( s ). Тогда продифференцируем ( 2 ) :
φ n +1 ( s ) = φ n ( φ ( s ) ) φ ( s ) φ1 ( 1 ) = ∑ Pk = 1
s = 1: φ n +1 ( 1 ) = φ n ( 1 ) φ ( 1 ) ( 4 ) k = o
Из соотношения ( 4 ) получаем рекурентную формулу
φ n ( 1 ) = [ φ ( 1 ) ] n
Но m = φ ( 1 ) = М ξ 1 – среднее число потомков от одной частицы.
Тогда получаем формулу математического ожидания среднего числа потомков в n –том поколении:
М η n = [ М ξ 1 ] n = m n ( 5 )
Найдем дисперсию.
Если обозначить σ 2 = D η 1 = D ξ 1 = ( η 0 = 1 ) – дисперсия числа частиц в 1-ом поколении, то дисперсия числа в n –том поколении:
D η n
= σ 2 m n
– 1 , m
≠ 1
( 6 )
n σ 2 , m = 1
Замечание. Если начальное число частиц η 0 = i 0 1 , то вместо формулы ( 5 )
имеем:
М η n = i 0 m n
Исследование вероятности вырождения ветвящегося процесса
Состояние { 0 } поглощающееся, то есть из η n = 0 η n + k = 0, k 1.
Обозначим q k = Р ( η n = 0 ) = φ n ( 0 ) свободный член нашего ряда; вероятность вырождения в момент n (или на n – том шаге); n 1.
Заметим. Если Р0 = 0 = Р ( ξ 1 = 0 ) (т.е вероятность числа потомков равна нулю), то
q n = 0 (вырождение не наступит).
Предположим, что η 0 = 1. Применим функцию ( 3 ), которая верна для противоположного случая.
Пусть s = 0, тогда из ( 3 ):
φ n +1 ( 0 ) = φ ( φ n ( 0 ) ) q n +1 = φ ( q n ) ( 7 ).
Предположим, что 0 p 0 1
(если р 0 = 1 , то вырождение наступает сразу, его рассматривать не имеет смысла).
0 p 0 1
Тогда ∑ p i = 1 – p 0 0
i = o
Среди p i (const.) непременно есть положительные, т.е. у нас с вероятностью больше нуля есть хотя бы один потомок.
Рассмотрим производную:
φ ( s ) =∑ k Рk S k - 1 0 при 0 s ≤ 1 ( в силу того, что среди pk есть
k = 1
положительные). Будем считать, что наш ряд сходится абсолютно.
Тогда φ ( s ) – строго возвратно при 0 s ≤ 1.
Замечание. Вернемся к последовательности { q n }:
q 1 = φ 1 ( 0 ) = р 0 0, на 1-ом шаге вероятность попасть в состояние 0
(потомков не останется)
из ( 7 ): q 2 = φ ( q 1 ), но при этом φ ( s ) возрастает и q 1 0.
Тогда получается φ ( q 1 ) φ ( 0 ) = φ 1 ( 0 ) = q 1 q 2 = φ ( q 1 ) q 1 (первый
шаг индукции).
Предположим, что на каком-то n выполнено аналогичное свойство, т.е. q n q n – 1
для некоторых n > 2.
Докажем, что это выполнено для q n + 1 , т.е.
( 7 ) ( 7 )
q n + 1 = φ ( q n ) > φ ( q n - 1 ) = q n
q n + 1 > q n , n ≥ 1 { q n } – строго возрастающая последовательность.
Эта последовательность ограничена сверху ( q n ≤ 1 ). Тогда
lim q n = - предельная вероятность вырождения.
n→ ∞
В
Лемма ( Абеля ). Если ∑ a k < , то lim ∑ a k S k = ∑ a k
k = 0 s 1 k = 0 k = 0
Кроме того заметим, что φ ( s ) – непрерывная. В соотношении ( 7 ): q n + 1 = φ ( q n )
Перейдем к lim: n = φ ( )
Выпишем уравнение s = φ ( s ) ( 8 )
Результат: - корень уравнения ( 8 ).
Докажем, что он является наименьшим корнем.
Теорема. - наименьший положительный корень уравнения ( 8 ) на отрезке ( 0, 1].
Доказательство. Пусть s 0 положительный корень уравнения ( 8 ):
s 0 = φ ( s ) ; s 0 1
q 1 = φ ( 0 ) = р 0 < s 0 ( т.к. φ – возрастает, а s 0 > 0 ) = s 0 q 1 s 0.
Предположим, что для некоторых n 1 выполнено аналогичное неравенство: q n s 0.
Заметим, q n + 1 = φ ( q n ) < φ ( s 0 ) = s 0 q n + 1 < s 0 вся последовательность ограничена сверху: q n s 0 , n 1.
Тогда предел этой последовательности
= lim q n s 0.
n 1
Что и требовалось доказать.
Д
Иначе: = ∑ Рk = 1 - ( р 0 + р1 ) > 0 среди { Рk, k r ) есть положительные числа
k = r
(потомков более двух и два).
Возьмем вторую производную:
φ
k = r
С точки зрения уравнения ( 8 ) эта функция может пересекать s не более, чем в двух точках, т.е.
Г
рафики
функций y = s
и y = φ
( s ) пересекаются не более
чем в двух точках, при этом одна из точек
– это 1, т.к. φ
( 1 ) = 1.
|
|
|
p 0
|
|
|
|
|
|
|
φ (s) |
φ (s) |
|
|||||
|
|
|
||||||
|
1 s 1 s p 0 = 0 1 s |
|||||||
p
0
1) 0 < < 1 2) = 1 3) = 0
φ ( 1 ) = m > 1 φ ( 1 ) = m ≤ 1 вырождение не
(наличие угла наклона) наблюдается
Лекция № 3
Марковские процессы с непрерывным временем и дискретным множеством
состояний
ξ ( t ) – случайный процесс, t 0, + ) – время, Х = { 0, 1, 2, … } – множество состояний (конечно или счетно).
Определение. Случайный процесс ξ ( t ) будет называться марковским, если
выполнены следующие соотношение:
Р (ξ ( t + r) = j | ξ ( t 0 ) = i 0 , ξ ( t 1 ) = i 1 , … , ξ ( t n ) = i n , ξ ( t ) = i ) =
Р (ξ ( t + r) = j | ξ ( t 0 ) = i ), где 0 < t 0 < t 1 < … < t n< t < t + r , i 0 , i 1 , …, i n , i , j X
t 0 , t 1 - прошлое
t - настоящее.
Функция Р i j ( s, t ) = Р ( ξ ( t ) = j ( ξ ( s ) = 1 ), 0 ≤ s < t , i, j X.
Определяет поведение процесса и называется функцией переходных вероятностей.
Свойства этой функции:
-
Не отрицательность
0 Р i j ( s, t ) < 1, s < t , i, j X.
-
Условие нормировки
∑ Р i j ( s, t ) = 1
j х
Как и в дискретном времени конечномерное распределение процесса может быть выражено через эти вероятности перехода
Р ( ξ ( t 1 ) = i 1 , ξ ( t 2 ) = i 2 , … , ξ ( t n ) = i n , ξ ( t 0 ) = i 0 ) =
= Р ( ξ ( t 1 ) = i 1 | ξ ( t 0 ) = i 0 ) P ( ξ ( t 2 ) = i 2 | ξ ( t 1 ) = i 1 ) …
… Р ( ξ ( t n ) = i n | ξ ( t n - 1 ) = i n - 1 ) = P i 0 , i 1 ( t 0 , t 1 ) P i 1 , i 2 ( t 1, t 2 ) … P i n -1 , i n ( t n-1, t n )
Это доказывается с помощью условных вероятностей и марковского свойства.
Уравнение Колмогорова - Чепмена
Р i j ( s, t ) = ∑ Р i k ( s, u ) = Р k j ( u , t ) ; 0 ≤ s < u < t , i, j X.
k х
Будем рассматривать
величины, зависящие
от
длительности времени
i Х
j
┬──┬─────┬─────┬───►
0 s φ t время
Определение. Марковский процесс будет называться однородным, если вероятность перехода будет зависеть от разности аргументов.
Р i j ( s, t ) = Р i j ( t - s ) = Р i j ( τ ) , τ = t – s > 0
Замечание. Будем предполагать, что для переходных вероятностей выполнено
свойство непрерывности в нуле, т.е.
lim Р i j ( Δ ) = δ i j =
Δ 0 ↑
символ вероятности Кронекера
В дальнейшем считаем, что все эти свойства выполнены.
Теорема. функция Р i j ( t ) равномерно непрерывна.
(доказательство с помощью свойства и элементарных преобразований).
Без доказательства.
Введем следующие характеристики
a i j = lim , i j ( 1 )
Δ 0
a i j = lim - время, Р i j - вероятность перехода ( 2 )
Δ 0
Теорема 1. Для i X предел
lim = a i существует и может быть как конечным ( a i ≤ ).
Δ 0
Без доказательства.
Теорема 2. Для i, j X, i j предел a i j и конечен ( a i j ).
Без доказательства.
Замечание. Эти соотношения ( 1 ) и ( 2 ) можно записать одним, а именно так:
символ вероятности Кронекера
a i j = lim
Δ 0
a i i = - a i i
a i j – называется интенсивностями перехода из i в j .
a i – называется интенсивностями выхода.
Эти характеристики называются инфинитезимальными.
В асимптотическом виде:
Р i j ( Δ ) = a i j Δ + o ( Δ ) , Δ → 0 ( 3 )
Р i i ( Δ ) = 1 - a i Δ + o ( Δ ) , Δ → 0 ( 4 )
Соотношение между инфинитезимальными характеристиками. В общем случае имеет место соотношение:
∑ a i j ≤ a i , i X ( 5 )
j i
Докажем ( 5 ): Запишем соотношение нормировки:
∑ Р i j ( ) = 1
j х
Перенесем один член в правую часть, там где i j :
∑ Р i j ( ) = 1 - Р i i ( ).
j i
Если ∑ конечно, то можно перейти к пределу. Но у нас не все известно надо найти оценку. Возьмем конечное N i:
∑ Р i j ( ) < 1 - Р i i ( ).
j = 0
Так как ∑ конечно, можно поделить на и перейти к пределу по .
lim ∑ ≤ lim
Δ
0
j = 0
Δ
0
∑ а i j ≤ a i ( N – произвольно )
j = 0
Т. о из этого переходим к ( 5 ), т.к. верно для N.
Что и требовалось доказать.
В конечном случае ( 5 ) имеет точное равенство, т.е.
∑ а i j
= a i
конечно Х.
Определение.
Если для i X, справедливо равенство
∑ а i j
= a i
,
то марковский процесс называется регулярным (консервативность).
Дифференциальное уравнение Колмогорова для переходных вероятностей Р i j
Из уравнения Колмогорова –Чепмена следует два соответствия:
Р i j ( t + ) = ∑ Р i k ( t ) Р k j ( ) ( 1 ) ┬───┬──────────┬───┬──►
k х 0 t t +
P i j ( t + ) = ∑ Р i k ( ) Р k j ( t ) ( 2 ) ┬───┬───────────┬───┬──►
k х 0 t t +
Вычитаем из обеих частей ( 1 ) и ( 2 ) Р i j ( t )
P i j ( t + ) - Р i j ( t ) = ∑ Р i k ( t ) Р k j ( ) - Р i j ( t ) ( 3 )
k х
P i j ( t + ) - Р i j ( t ) = ∑ Р i k ( ) Р k j ( t ) - Р i j ( t ) ( 4 )
k х
Выделим из ∑ член, где индексы одинаковые
( 3 ) P i j ( t + ) - Р i j ( t ) = Р i j ( t ) Р j j ( ) - Р i j ( t ) + ∑ Р i k ( t ) Р k j ( ) ( 5 )
k j
( 4 ) P i j ( t + ) - Р i j ( t ) = Р i i ( ) Р i j ( t ) - Р i j ( t ) + ∑ Р i k ( ) Р k j ( t ) ( 6 )
k i
P i j ( t + ) - Р i j ( t ) = [ 1 - Р j j ( ) ] Р i j ( t ) + ∑ Р i k ( t ) Р k j ( ) ( 7 )
k j
P i j ( t + ) - Р i j ( t ) = [ 1 - Р i i ( ) ] Р i j ( t ) + ∑ Р i k ( ) Р k j ( t ) ( 8 )
k i
Если разделить на и перейти к lim, то справа будет производная.
Если множество состояний Х конечно, то можно перейти к пределу и сделать следующий вывод:
( 7 ) P i j ( t ) = - a j P i j ( t ) + ∑ Р i k ( t ) a k j , i , j X ( 9 )
k j
( 8 ) P i j ( t ) = - a i P i j ( t ) + ∑ Р k j ( t ) a i k , i , j X ( 10 )
k i
Получили обратную систему дифференциальных уравнений Колмогорова для
переходных вероятностей.
Теорема 1. Для регулярного марковского процесса ( t ) справедлива обратная
система дифференциальных уравнений Колмогорова для счетного
множества состояний Х.
Теорема 2. Пусть ( t ) – регулярный марковский процесс со счетным множеством
состояний Х. Предположим также, что для i X справедливо
соотношение :
∑ Р i k ( t ) a k < , t 0.
k х
Тогда имеет место прямая система дифференциальных уравнений
Колмогорова.
Замечание. В конечном случае эти теоремы справедливы.
Лекция № 4
Уравнение Колмогорова для вероятностей состояний марковского процесса
Введем следующие характеристики
p k ( t ) = P ( ( t ) = k ), k X, t 0 – вероятности состояний марковского процесса.
Запишем соотношение:
p k ( t + ) = ∑ p i ( t ) p i k ( ) (из формулы полной вероятности)
i х
p k ( t + ) - p k ( t ) = p k ( t ) [ p k k ( ) – 1 ] + ∑ p i ( t ) p i k ( )
i k
Делим на и → 0, т.е. берем предел:
( 1 ) p k ( t ) = - a k p k ( t ) + ∑ p i ( t ) a i k ; k X – система
i k
дифференциальных уравнений Колмогорова для вероятностей состояний.
Свойства такие же, как и у прямой системы
Свойства траекторий марковского процесса
Ступенчатые функции, функции разрыва
Распределение времени пребывания марковского процесса в фиксированном состоянии.
Пусть ( 0 ) = k (фиксированное) – начальное состояние или p k ( 0 ) = 1.
В силу марковости и однородности процесса распределение времени пребывания процесса не зависит от момента начала наблюдений.
Вернемся к системе уравнений ( 1 ). Заметим, что интенсивности a i k связаны с переходами процесса из состояния i в фиксированное состояние k , т.е. с поведением процесса в будущем ( после ухода из k ). Эволюция процесса не зависит от будущего. Т.о. распределение времени пребывания нашего процесса ( t ) в состоянии k не зависит от интенсивности a i k , i k .
Полагаем, (если не зависит их можно выбрать какими угодно), что в соотношении ( 1 ) все a i k = 0, i k . Тогда из ( 1 ) такое: p k ( t ) = - a k p k ( t );
p k ( 0 ) = 1 ( 2 )
Задача 2 - это задача Коши, которая имеет следующее решение:
p k ( t ) = e - a k t ; t ≥ 0, k – фиксированное.
Заметим, что есть время пребывания Θ в фиксированном состоянии и вероятность:
P ( Θ > t | ( 0 ) = k ) = P ( ( t ) = k ) (т.к. Θ – время пребывания до первого
выхода ).
Тогда очевидно, что
P ( Θ > t | ( 0 ) = k ) = e - a k t ; k X (первый вывод).
Вероятности перехода марковского процесса в моменты изменения состояния.
Для описания марковского процесса нам необходимо время пребывания и закон, по которому происходит изменение состояния. Введем вероятность:
α i j = lim Р ( ( t + Δ ) = j | ( t ) = i , ( t + Δ ) ≠ i ) , i ≠ j
Δ 0
Если этот предел , то его называем вероятностью перехода из i в j в момент изменения состояния процесса.
Рассмотрим следующую вероятность:
условная вероятность
Р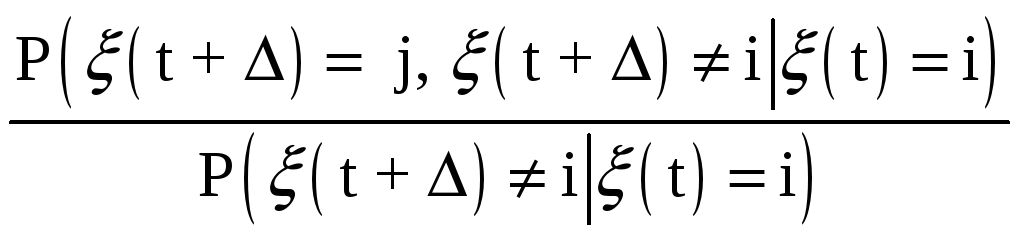
( ( t + Δ ) = j
| ( t ) = i
, ( t + Δ ) ≠ i
) ==================
Δ
= = I
Заметим, что ( ( t + Δ ) = j ) ( ( t + Δ ) ≠ i ), i ≠ j ,
т.о. пересечение двух событий, есть более узкое событие и тогда
Р ( ( t + Δ ) = j , ( t + Δ ) ≠ i | ( t ) = i ) = Р ( ( t + Δ ) = j | ( t ) = i )
I = =
Поделим числитель и знаменатель на и перейдем к пределу:
α i j = lim = lim = ( i ≠ j )
Δ 0 Δ 0
Если наше состояние i является регулярным, т.е.
a i = ∑ a i j , и при этом a i < , то
j
i
∑ i j = ∑ = 1 , т.е. { i j , i ≠ j } – распределение вероятностей.
j i j i
Терминология.
Cостояние i будет называться мгновенным, если интенсивность выхода из него равна ( a i = ). Момент ожидания в этом состоянии равен нулю
( М ( Θ | ( 0 ) = i ) = 0 и P ( Θ < t ) = 1 - e - a t = 1, t > 0 .
Время пребывания в этом случае равно нулю с вероятностью 1.
Cостояние i будет называться поглощающим, если a i = 0. Тогда математическое
ожидание ( М ( Θ | ( 0 ) = i ) = = . Процесс навсегда остается в этом состоянии с вероятностью = 1.
Свойства траекторий процесса.
1
.
Пусть в начальный момент процесс
находится в состоянии i (
( 0 ) = i
). Тогда время пребывания в этом состоянии
P ( Θ < t
| ( 0
) = i ) = 1- e
- a
i
t
, t ≥ 0
.
2. В момент времени изменение состояния t 1 = Θ происходит переход из i в j с
вероятностью i j = .
3. При условии ( t 1 ) = j распределение P ( Θ < t | ( t 1 ) = j ) = 1- e – a j t , t ≥ 0 .
4. В момент времени t 2 , т.е., когда завершается интервал t 1 + Θ , происходит
переход из j в k ( j ≠ k ) с вероятностью j j k = .
Далее процесс происходит аналогично.
Нарисуем траекторию процесса
-
Xj
(0) = i
( t 1 ) = j
( t 2 ) = k
Непрерывность справа.
Для моделирования этого процесса
необходимо реализовать экспоненц.
и дискретное распределения.
K
t 0
t 1 t 2
Лекция № 5
Важнейшие классы марковских процессов
-
Процесс гибели и размножения (ПГР)
Определение. ПГР будет называться однородный марковский процесс (t), t [ 0,),
X = { 0, 1, 2, …} вероятности перехода которого удовлетворяют следующим соотношениям:
1. Р i , i + 1 ( ) = i + 0 ( ) , 0; i 0;
2. Р i , i – 1 ( ) = i + 0 ( ) , 0; i 1;
3. Р i , i ( ) = 1 - ( i + i ) + 0 ( ) , 0; i 0,
где 0 = 0, 0 0, i 0, i 0, i = 1, 2, …
Замечание к определению.
В ПГР ( t ) инфинитезимальные характеристики имеют следующий вид:
i ,
j = i +
1 ,
α i j = i , j = i - 1 , и α i = i + i
0, в остальных случаях | j i |
Время пребывания ( t ) в состоянии i :
P ( Θ < | ( 0 ) = i ) = 1- e - ( i + i )
Вероятность перехода в момент изменения состояния:
, j = i + 1
i j = , j = i - 1
0, в остальных случаях
т.е. траектория состояния имеет ступенчатую функцию. Изменение состояния
происходит со скачками 1.
-
t
Траектория – типичная, т.е.
наиболее вероятная.
Случайность - в длине ступеньки (это случайная величина, которая распределена экспоненциально).
Если рассмотреть частные случаи:
-
i = 0, то процесс называется процесс чистой гибели ( i 0 )
-
i = 0 – процесс чистого размножения ( i 0 )
Замечание к определению. В силу свойств 1 – 3 наш процесс ГР является регулярным, т.е. выполняется условие регулярности
a i = ∑ a i j = i + i
j i
Получим уравнение Колмогорова для вероятностей состояний процесса. Напомним уравнение Колмогорова в общем виде:
P k ( t ) = - a k p k ( t ) + ∑ p i ( t ) a i k ; k X – система
i k
Выполним эту систему уравнений:
|
0 = 0 |
P 0
( t ) = -
0 p 0
( t ) +
1
p 1
( t )
( 1 )
P k ( t ) = - k - 1 P k - 1 ( t ) - ( k + k ) P k ( t ) + k + 1 P k + 1 ( t ) , k ≥ 1.
Заметим, что нулевое уравнение получается при условии, что 0 = 0 ( по условию ).
А переходы в состоянии 0 можно получить только из 1.
Заметим , что система уравнений может быть, как конечной, так и бесконечной, т.к. состояния могут быть как конечны, так и бесконечны.
Нарисуем граф вышесказанной системы:
0
1
k– 1
k
k + 1
N- 1
|
|
|
1 |
|
|
|
|
|
|
|
N |
0
k - 1
K
k
+ 1
1
2
k
k
+ 1
k
+ 2
N
конечное Х
Заметим, что для системы ( 1 ) можно записать стационарное решение. Пусть предельное распределение P k = lim P k ( t ) , ∑ P k = 1.
t 0 k х
Чисто формально перейдем к пределу по t в соотношении - Х ( 1 ):
0 = -
0 p 0
+
1
p 1
,
k = 0
0 = - k - 1 p k - 1 - ( k + k ) p k + k + 1 p k + 1 = 0, k ≥ 1. ( 2 )
Заметим, Z k = - k - 1 p k - 1 + k p k , k = 1, 2, …
Тогда из соотношения ( 2 ) через Z k можно получить:
Z 1
= 0, k = 1, 2, …
Z k + 1 - Z k = 0 , k = 1, 2, … Z k = 0, т.е. мы получаем все Z k = 0
Тогда
- k - 1 p k - 1 - k p k = 0, k = 1, 2, …
Заменяем это соотношение на рекурентное:
P k = P k – 1 = P k – 2 k = 1, 2, …
Тогда отсюда следует, что
P k = p 0 ; k 1
Введем вспомогательную константу
k = , . k 1
0 = 1
Тогда получаем следующее соотношение:
P k
=
k p 0
, k
0
- формула для предельного
распределения ПГР 
Из условий нормировки: ∑ P k = ∑ k p 0 = p 0 ∑ k = 1
k = 0 k = 0 k = 0
Это и есть окончательная формула для предельного распределения ПГР.
Теорема. Для регулярного ПГР условие сходимости ряда ∑ k является
k = 0
необходимым и достаточным для существования предельного распределения.
Достаточное условие для сходимости ряда ∑ k< ↔ предельное распределение.
k = 0
Если ряд расходится, то
предельного распределения.
Предположим, что все сомножители < q < 1 , i 1, т.е. ограничены сверху
о 
Тогда k = < q k ∑ k ∑ q k < .
k = 0 k = 0
Это означает, что интенсивность перехода на 1 вверх всегда меньше, чем интенсивность на 1 вниз, т.е. k - 1 k .
Эти четыре пункта называются конструктивным определением марковского процесса и является теоретической основой для стахостического моделирования этого процесса.
Лекция № 6
ПУАССОНОВСКИЙ ПРОЦЕСС
О
пределение
1. Пуассоновским случайным процессом
называется однородный Марковский
Процесс (МП)
( t
), t
[ 0,),
х = { 0, 1, 2, …}, который выполняется :
1. Р i
, i + 1
(
) =
+ 0 (
) ,
0; i
0; 2
2. Р i
i
(
) = 1 -
+ 0 (
) ,
0; i
0; 1
3.
( 0 ) = 0 или
Р
{
( 0 ) = 0 } = 1
t1 t 2 t 3 t
Вариант определения 1. Пуассоновским процессом (ПП) будет называться процесс чистого размножения, для которого k = , k 0.
Свойства Пуассоновского процесса (ПП):
1. Время пребывания в fix состоянии имеет экспонентное распределение с
параметром
P { < х } = 1 – e - . не экспонентно { }
2. Интенсивность перехода α i j =
3. Вероятности перехода в момент изменения состояния:
i j =
Вероятности состояний Пуассоновского Процесса (ПП): P k ( t ) = { ( t ) = k }, k 0.
Уравнение Колмогорова (общее): p k ( t ) = - a k p k ( t ) + ∑ p i ( t ) a i k .
i k
Для ПГР: p 0 ( t ) = - 0 p 0 ( t ) + 1 p 1 ( t )
p i ( t ) = - i - 1 p i - 1 ( t ) + ( i + i ) p i ( t ) + i + 1 p i + 1 ( t ) ,
i = 0, i = 1, i ≥ 0.
p 0
( t ) = -
p 0
( t )
p i ( t ) = - p i - 1 ( t ) - p i ( t ) ( 1 )
Начальное условие из пункта 3 в определении 1
p 0 ( 0 ) = 1, p i ( 0 ) = 1.
Воспользуемся методом производящих функций
( z , t ) = ∑ p k ( t ) z k – производящая функция
k = 0
Умножим каждое из выражений в ( 1 ) на z i и просуммируем:
= z ( z , t ) - ( z , t ) ( 2 )
при t = 0 все члены равны нулю.
( z , 0 ) = 1
Перепишем ( 2 ): = (z - 1) ( z , t )
Решение этого уравнения: ( z , t ) = e (z - 1) t = e - t e z t =
=
e -
t ∑ z
k , (сравниваем
с
( z , t ) = ∑
p k
( t ) z
k )
k = 0 k = 0
P k ( t ) = e - t , k = 0, 1 ( 3 )
в момент времени t в состоянии k мы находимся с вероятностью P k ( t ) с параметром t.
Вектор { P k ( t ) } , k 0 образует дискретное распределение Пуассона с параметрами t . Из свойств Пуассоновского распределения M ( t ) = t, D ( t ) = t.
Вероятности перехода Р i j ( t ) = P { ( t ) = j | ( 0 ) = i }
Вспомним прямую систему Колмогорова:
P i j ( t ) = - a j p i j ( t ) + ∑ p i k ( t ) a k j , i, j 0.
k j
Условия существования прямой системы Колмогорова в случае счетного множества
состояний выполнены.
Система: a j = , j 0.
k j =
П
олучим:
p i
j (
t ) = -
p i
j (
t ) +
p i
, j - 1
( t ) , i
0 , j
1.
p i , 0 ( t ) = - p i , 0 ( t ) , i 0 , j = 0 ( 4 )
В
k = 0
Умножим в ( 4 ) каждое уравнение на z i и суммируем.
Получим:
= z i ( z , t ) - i ( z , t )
= ( z – 1 ) i ( z , t ) ( 5 )
k = 0
Общее решение уравнения ( 5 ): ( z , t ) = c e - ( z – 1 ) t
i ( z , t ) = z i e - (z - 1) t
Р
азлагаем
( z , t ) по
степеням
:
i ( z , t ) = z i e (z - 1) t = z i e - t e z t = ∑ z k + i e - t = =
k = 0
= ∑ e - t z ( 6 )
j = 1
Сравнивая с общим видом производящей функции, получим:
0, i <
j
Выражает вероятности
перехода для ПП
P i j ( t ) = e - t , j i ( 7 )
Замечание. Вероятности перехода обладают свойством однородности не только по времени, но и “по состояниям”, т.к. эти вероятности P i j зависят только от разности j и i .
Распределение приращений Пуассоновского Процесса (ПП)
P { ξ
( t
) - ξ ( 0 )
= k } = Р {
( t ) = k
} = P k
( t ) = e
-
t
совпадает с P k
( t )
P { ξ
(
+ t
) - ξ ( t )
= k } ===========
за время произошло k скачков
∑ P{ ξ ( + t ) - ξ ( t ) = k | ( t ) = s } Р { ( t ) = s } = { в силу того, что траектории
k = 0
не убывающие } = ∑ P{ ξ ( + t ) = k + s | ( t ) = s } Р { ( t ) = s }
s = 0
Заметим, что
P{ ξ ( + t ) = k + s | ξ ( t ) = s } = P 1 , k + 1 ( , t + z ) = { однородность по времени } = = P 1 , k + 1 ( t ) = { однородность по состоянию } =
P k ( t ) = e - t ( 8 )
C учетом ( 8 ) P{ ξ ( + t ) - ξ ( t ) = k } = ∑ Pk ( t ) Р0 { ( t ) = s } =
s = 0
сумма равна 1
P k ( t ) = e - t
не зависит от s
Лекция № 7
Пуассоновский Процесс обладает свойствами независимости приращения на временном интервале.
Распределение вероятности приращений Пуассоновского Процесса не зависит от интервала времени, а только от длины интервала.
Пусть t n - момент n – го скачка Пуассоновского Процесса, k = 1, 2, …, t 0 = 0.
В
момент t n
n – го
скачка процесс переходит в состояние
n (т.е. скачок из ( n
– 1 ) в n ).
ξ ( t n ) = n , ξ ( t n - 0 ) = n - 1
t n - случайная величина ; х - фиксированное число.
t n х , т.е. до момента х произошло по крайней мере n скачков.
дополнение
( t n х ) = ( ξ ( х ) = k ) = ( t n х ) = ( ξ ( х ) = k ) событий
k = n k = 0
n - 1
P ( t n х ) = 1 - P ( ( ξ ( х ) = k ) ) = { т.к. несовместны } =
k
= 0
при каждом k эти события несовместны
n
- 1
= 1 - ∑ P ( ξ ( х ) = k ) ) = 1 - ∑ e - х , n 1. ( 9 )
k = 0
k
= 0
если продифференцировать это выражение по х получается плотность -распределения.
В частности, если n = 1, получим P ( t 1 х ) = 1 - e - х ( момент первого скачка имеет экспонентное распределение ).
Заметим, что если рассмотреть структуру t n :
n
t n = ∑ k , k = t k - t k – 1 , k = 1, 2, … , n
k = 1
( k – интервал между скачками процесса )
P ( k y ) = 1 - e - y
k – время пребывания на k – 1 ступеньке.
t n – сумма независимых одиночных распределений случайных величин, каждая из
них имеет экспонентное распределение.
Формула ( 9 ), как формула для такого распределения, называется распределением Эрланга с параметром ( может быть параметр n ).
Марковские процессы с непрерывным временем и непрерывным множеством
cостояний
|
|
|
|
|
|
Р { t 1 < x | ξ ( T ) = 1 } = =
Интервалы не пересекаются, и события независимы
= = |
|
|
|
|
|||
|
0 |
t 1 x T t |
|
|||
-
1
T
Пусть задан марковский процесс ( МП ) ( t ) , t T [ 0,) – - время непрерывное, х – множество состояний (вещественная прямая Х = R 1 , может в нем быть В – - алгебра ( сигма – алгебра ) борелевских множеств в R ). Такой МП тоже должен задаваться вероятностями перехода, но уже другими.
Обозначим P ( s, х ; t , B ) = Р ( ( t ) B | ( s ) = х ) s, t T , s < t, х Х,
B B (борелевское множество). Эта функция называется вероятностью перехода процесса ( t ).
Теорема 1. Пусть на множестве значений временного параметра T [ 0,) Х = R c
- алгеброй борелевских В определено семейство неотрицательных функций Р ( s, х , t , B ), s, t [ 0,) , s < t, х R , B B борелевские, которые удовлетворяют следующим условиям:
1.) Для fix s, х , t функция Р ( s, х ; t , B ) является вероятностной мерой по В;
-
Для fix s, t ; В - функция Р ( s, х ; t , B ) измерима по х (борелевская
функция).
3.) Для 0 ≤ s < u < t (параметр времени),
В B справедливо соотношение:
Р ( s, х ;
t , B
) = ∫ Р
( s, х ; u, d y ) P (u, y ; t
, B ) ( 1 )
( т.е. были в состоянии х. В момент u мы находились в некотором В В ,
содержащем y. )
(Уравнение Колмогорова - Чепмена )
Пусть также на пространстве ( R, B ) вероятностная мера P0 ( Γ ) , Γ B
Тогда такое вероятностное пространство ( , , Р ) и случайный процесс на
нем ( t ) = ( , t ) , , t T [ 0,) такие, что
математическая вероятность
борелевские множества
0 t 0 t 1 … t n ; В 0 , В 1, … , В n В , n 1
выполняется следующее соотношение:
Р ( ( t 0 ) В 0 , ( t 1 ) В 1 , … , ( t n ) В n =
= ∫ Р 0
( d y 0
) ∫ P ( t 0
, y 0
; t 1 d y
1 ) … ∫
P ( t n
- 1,
y n
- 1
; t
n d y
n
) ( 2 )
< формулировка теоремы закончена >
Построенный процесс ( t ) является марковским с непрерывным временем = [ 0,) и множеством состояний Х = R.
Теорема 1 (о существовании марковского процесса) выводится из теоремы Колмогорова (о существовании случайного процесса с заданной фиксированной системой согласованных вероятностных мер).
|
|
х
|
X
|
|
|
B
|
Иллюстрация к соотношению 1 |
|
|
||||||
|
s u t |
||||||
Пусть переходная вероятность Р ( s, x ; t , B ), как вероятностная мера по В является абсолютно непрерывной относительно меры Лебега (мера пространства R1 ). Фактически это означает, что такая функция р ( s, x ; t , y ), y R, такая, что для борелевского множества В В имеет место равенство
Р ( s, x ; t
, B )
= ∫ р
( s, x ; t
, y ) d y.
р ( s, x ; t , y ), где t T , s < t, x , y R - называется плотностью вероятности переходов ( t ).
Тогда уравнение Колмогорова - Чепмена ( 1 ) можно записать через эту плотность следующим образом:
Р
( s, x ; t
, y ) = ∫ p ( s, x ; u , z )
p ( u , z ; t ,
y ) d z ; s < u < t
( 3 ) -
производная Радокса – Никодима.