Задание 1.4:

Построение графиков зависимостей статических и дифференциальных сопротивлений от тока и напряжения, а также дифференциальной проводимости прямой ветви ВАХ диода от напряжения можно провести по формуле, так как она хорошо аппроксимирует реальную ВАХ диода. В таблице 1.4 даны значения соответствующих величин для построения графиков статистического сопротивления. Заполнение строк таблице, а так же все необходимые расчеты и построения, проводились по формулам:

_{Статическое сопротивление определялось как} .

Динамическое сопротивление определялось по формуле .

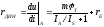_{Дифференциальная проводимость определяется как} .

1) Статическое сопротивление (Рисунок 1.6):

_{Таблица 1.4}

Uуточн, В	I, А	RСТ
0,255129	0,01	25,5129
0,294993	0,015	19,6662
0,327801	0,02	16,39005
0,363222	0,025	14,52888
0,397664	0,03	13,25547
0,465472	0,04	11,6368
0,487527	0,045	10,83393
0,514893	0,05	10,29786
0,550335	0,06	9,17225
0,671628	0,085	7,901506
0,717565	0,1	7,17565

_{Рисунок 1.6 Статистическое сопротивление.}

2) Динамическое сопротивление (Рисунок 1.7):

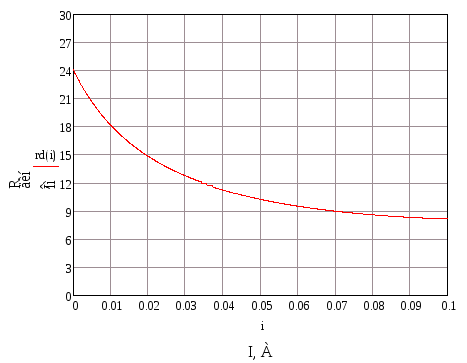
_{Рисунок 1.7 Динамическое сопротивление.}

3) Дифференциальная проводимость (Рисунок 1.9):

_{Рисунок 1.8 Дифференциальная проводимость.}

Задание 1.5:

Определим параметры кусочно-линейной модели диода для больших прямых и обратных значений напряжения (рисунок 1.9):

_{Рисунок 1.9 Параметры кусочно-линейной модели диода.}

Данная модель применяется только для больших значений напряжения (как прямого, так и обратного).

_{Рисунок 1.10 Осциллограммы тока и напряжения на диоде при подключении к нему гармонического напряжения с амплитудой N=1.}

Задание 1.6:

Определим область квадратичной модели диода. Для этого обратимся к графику дифференциальной проводимости от напряжения по прямой ветви ВАХ, изображенному на рисунке 1.8. На нем возьмем значения напряжения, а затем перенесем их на график ВАХ заданного диода и на нем получим значения тока (рисунок 1.9).

_{Рисунок 1.11 ВАХ заданного диода.}

Выделим на нем линейный участок и обозначим:

• точка a – это начало линейного участка;

• точка A – это середина линейного участка;

• точка b – это конец линейного участка.

Определим значения напряжений в этих точках. Затем, с помощью графика ВАХ заданного диода, изображенного на рисунке 1.9 определим значения токов. Данные сведены в таблицу 1.5.

_{Таблица 1.5}

	a	A	b
U, В	0,80	0,85	0,90
I, мА	25	31	38

Квадратичная модель: I=a₀+a₁U+a₂U².

Определим параметры квадратичной модели. Для этого составим систему уравнений и решим ее, затем построим график квадратичной модели совместно с ВАХ заданного диода. Построим квадратичную модель ВАХ диода (рисунок 1.12).

_{Рисунок 1.12 Квадратичная модель ВАХ диода.}

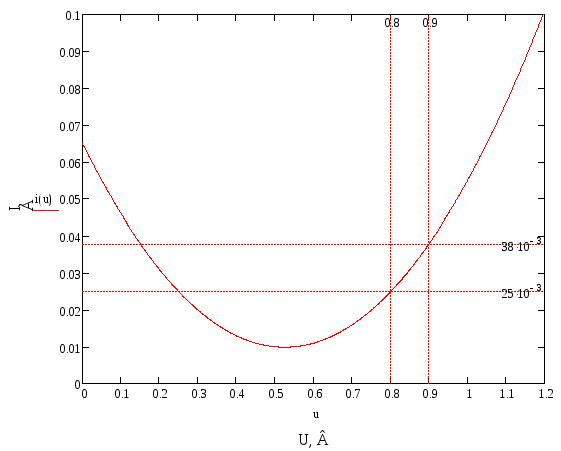
Квадратичная модель хорошо аппроксимирует ВАХ диода, однако основным ее недостатком является то, что она применима на маленьких интервалах.

Рисунок 1.13 Величины постоянного напряжения и амплитуды гармонического сигнала выбраны в области применения модели.

Из сопоставления графиков видно, что область применения квадратичной модели диода чуть больше, чем интервал от a до b.

Осциллограммы тока и напряжения на диоде при подключении к нему напряжения U=E_А+U_mcosωt, где величины постоянного напряжения и амплитуды гармонического сигнала выбраны в области применения модели, представлены на рисунке 1.13.