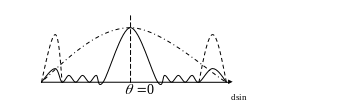
§2.7 Дифракционная решётка.
Рассмотрим экран в котором проделано N отверстий (щелей) ширина каждого из которого D
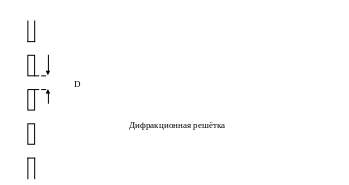
Пусть источник излучения S находиться на большом расстояние от решётки. Определим волновую функцию в точке p лежащей в волновой зоне с другой стороны решётки.
Волновая функция в точке p будет равно сумме волновых функций от каждого отверстия решётки. То есть каждая отверстие решётки мы рассмотрим как источник излучения.
Повторяем выводы §2.5 находим
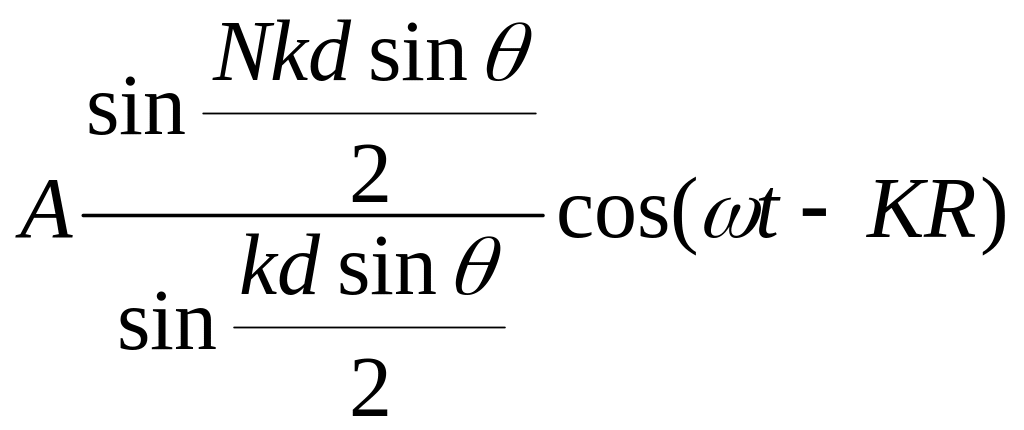
При определение амплитуды волновой функции в точке p
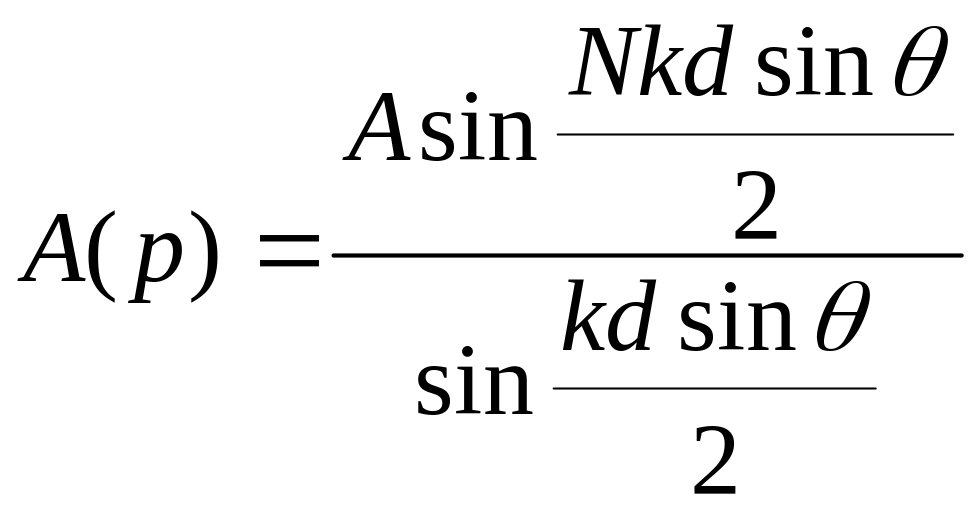
Необходимо учесть что каждый источник имеет конечный размер D и не является точечным, как в §2.5 . Для определения амплитуды излученя такого источника надо воспользоваться результатами §2.6, где была получена амплитуда
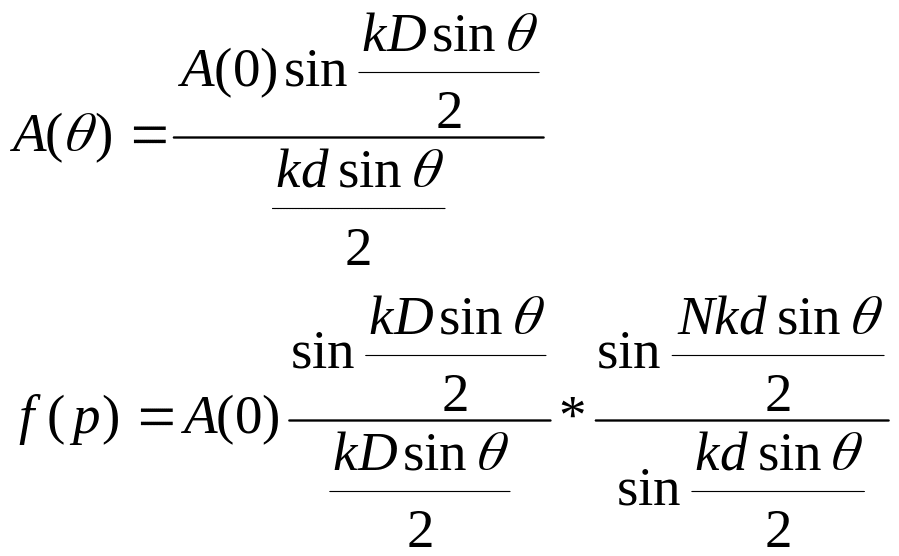
n=0
Положение главных максимумов определяет
исследование
и
зависит от длины волны излучения
за
исключением центрального.
Это свойство дифракционной решётки позволяет определить спектральный состав излучения. Если источник испускает волны с различной длиной то с помощью дифракционной решётки можно найти длины этих волн, так как условие главного максимума : и волны различной длины будут наблюдаться под разными углами
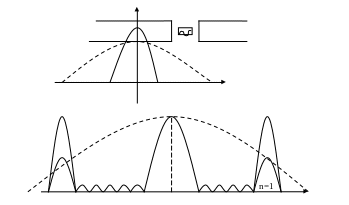
Максимумы первого порядка будут определять спектр первого порядка излучения.
n=2 – второй порядок спектра
Релей предложил критерий различимости
двух линий в спектре излучения линии
излучения будем считать различными
если главный максимум
совпадает с ближайшим минимумом другой
-
минимальный интервал длин волн, который
можно различить с помощью дифракционной
решётки.
-разрешительная
способность.
§2.8 Принцип Гюйгенса – Фринеля.
Дифракция Фринеля.
Если источник находиться на большом расстояние от экрана с отверстием, а точка наблюдения P также на большом расстояние, то наблюдается дифракция – дифракция Фраунгофера. Если нарушается хотя бы одно из условий то называется дифракция Фринеля.
Фринель дополнил принцем Гюйгенса следующим условие: для того чтобы найти волны в точке p надо разбить поверхность волнового фронта на бесконечно малые плоские участки ds. Тогда волновая функция в точке p будет равна сумме волновой функции излучаемых каждым участком.
Амплитуда в точке p будет равна сумме волны, что совпадает с принципом Гюйгенса.
Амплитуда волны излучаемая каждым
участком будет
А-амплитуда на поверхности волнового
фронта
-
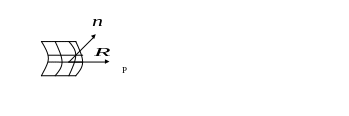
некоторые функции зависят
от нормали
и радиуса вектора R,
про который известно что она
уменьшается с увеличением угла.
В качестве примера принципа Гюйгенса-Фринеля рассмотрим сферически симметрическую задачу когда источник, центр отверстия и точка находятся на одной прямой
Предположим что источник находиться на большом расстояние от отверстия. Тогда волновой фронт в отверстия будет по принципу Фринеля будет равна сумме функций излучения небольшими участками.
Амплитуда колебаний
Тогда
В качеств бесконечно малых участков
поверхности ds выберем
тонкое кольцо радиусом
и толщиной
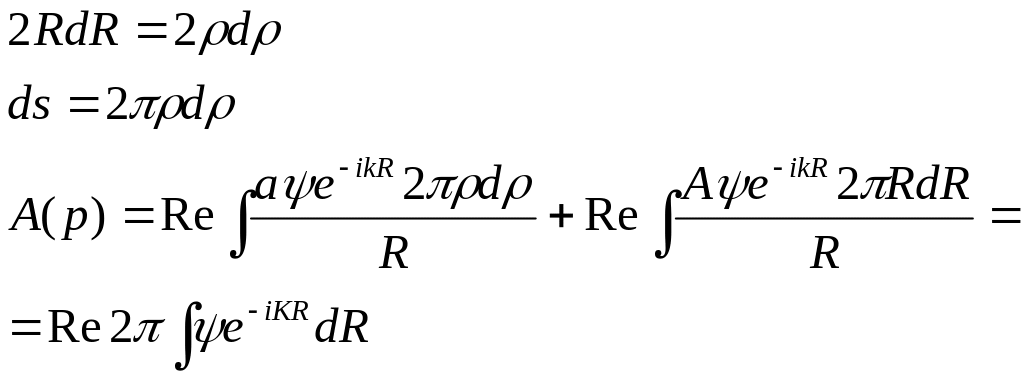
Таким образом амплитуда колебаний в точке p, будет пропорциональной реальной части интервала.
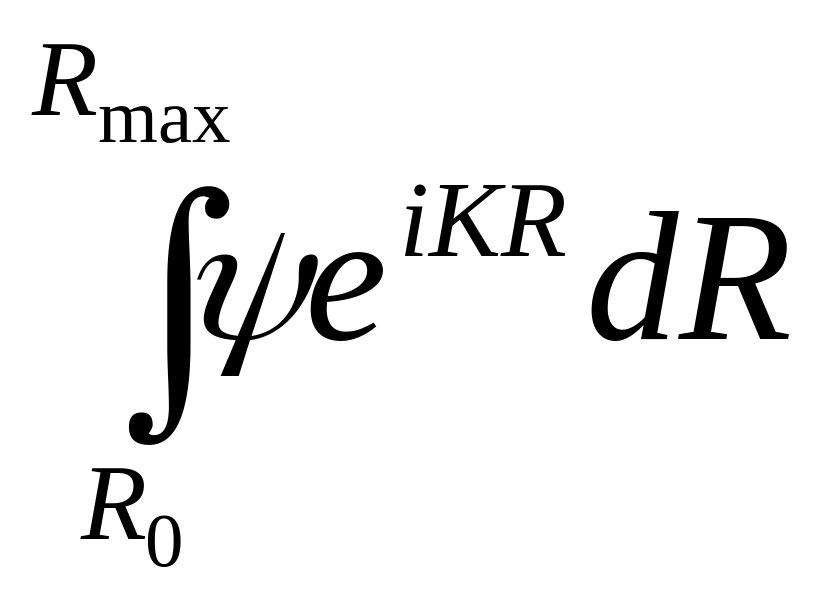
Для вычисления этого интеграла предположим сначала, что постоянна , тогда:
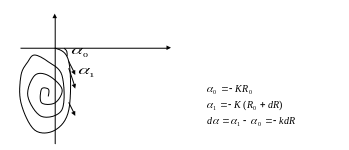
Таким образом предположим, что
то такой интеграл не сходится. Влияние
функции
приведёт к тому что каждый следующие
слагаемое будет меньше предыдущего и
в результате окружность деформируется
в спираль Фринеля . Если отверстия в
экране бесконечно большие то амплитуда
колебаний точки p будет
определяться радиусом окружности.
Фринель предложил разбить поверхность
волнового фронта на зоны( зоны Фринеля)
таким образом что расстояние до границ
зоны от точки p отличается
на
Легко заметить, что в первой зоне Фринеля сответсвует первая полуокружность спирали. Вторая зона Фринеля это вторая полуокружность спирали и тд.
Если отверстие в экране совместимо с
размером первой зоны Фринеля то
то есть в два раза больше чем без экрана,
а энергия при этом будет больше в 4 раза.
Рассмотрим радиус n-й зоны Фринеля
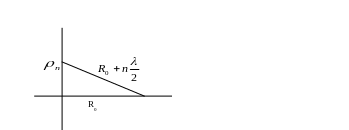
Если
Рассмотрим случай когда точка наблюдения
p находиться на очень
большом расстояние от экрана с отверстием.
будет очень большим и будет много больше
отверстия. То есть в отверстие экрана
попадает малая часть первой зоны, поэтому
амплитуда колебания в точке p
будет небольшой. Если точка p
будет приближаться к экрану (R0
уменьшиться) то радиус первой зоны
Фринеля будет уменьшаться и в отверстие
экрана будет попадать всё больше частиц,
то есть А будет увеличиваться, максимальная
амплитуда тогда когда радиус первой
зоны совпадёт с размером отверстия.
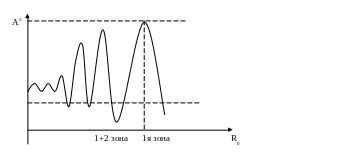
При дальнейшим приближение к экрану в отверстии будет помещаться вторая зона и амплитуда будет убывать.
Когда в отверстие экрана будет помещены обе зоны Фринеля А практически будет равна 0.
