§ 2.5 Многолучевая интерференция.
Рассмотри N источников
которые излучают сферические волны с
одинаковой амплитудой:
0
Рассмотрим между источниками d.
Определим волновую функцию в точке p находящеюся в волновой зоне.
При этом учтём
В точке p мы будем наблюдать волновую функцию с амплитудой
Рассмотрим случай когда
Вычислим
придел этой функции по, Лопиталю находим
что
.
Точно также мы можем определить амплитуду
волновой функции когда
При таких
будут наблюдаться max амплитуды,
которые называются главными. Если
кроме N, 2N …..
условие минимума.
Если
условие побочных максимумов.
Следует заметить, что А побочных
максимумов неодинакова в отличии от
главных
§2.6 Дифракция, принцип Гюйгенса
Рассмотрим точечный источник излучения S от которого распространяются сферические волны и которые находиться на большом расстояние от экрана с отверстием . Величина отверстия - D
Определим волновую функцию в точке p которая также находиться на большом расстояние от экрана , но с другой стороны.
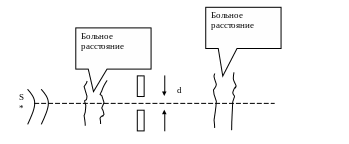
Гюйгенс предположил, что волновая
функция в точке p будет
складываться из волн, функция излучения
источника
и волн функции от экрана
Если экран закрыть пробкой:
То волновая функция в точке p
будет
-волны
функции от пробки
В результате
сложения функций в точке p
воловая функция будет
равна 0 .
То есть волновая функция в точке p ,будет с точностью до знака совпадать с волновой функцией излучаемой только пробкой.
Гюйгенс предположил каждую точку волнового фронта в отверстие экрана рассматривать как источник «вторичных» волн.
Волновая функция в точке p, будет равна сумме вторичных волн. Для того чтобы определить волновую функцию в точке p заметим что волновой фронт в отверстие экрана можно считать плоским так как источник находится на большом расстояние от него. Разобьём поверхность волн фронта на точечные источники излучения
Каждый
источник излучает сферическую волну с
одинаковой амплитудой, частотой и
одинаковой начальной фазой которую
будем считать равной нулю. Так как точка
p находиться в волновой
зоне то можно допустить, что амплитуда
волновой функции от каждого источника
одинаковы.
Повторяем выводы § 2.5 получаем
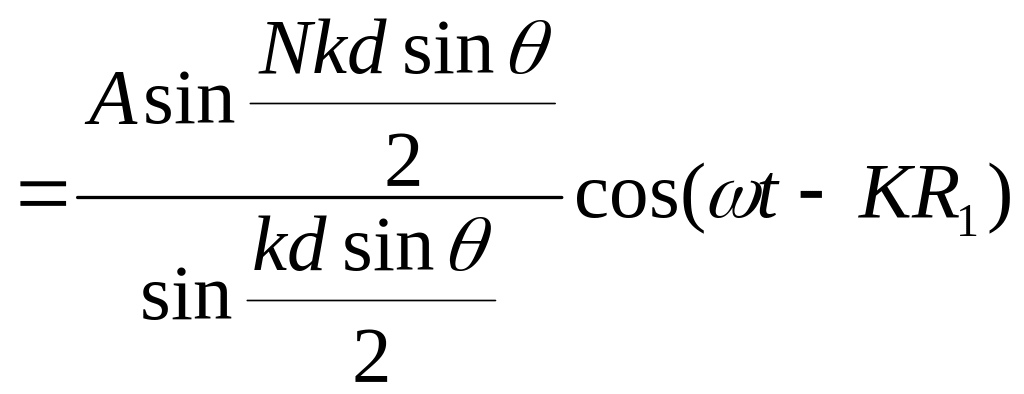Для
того чтобы определить
амплитуду волновой функции
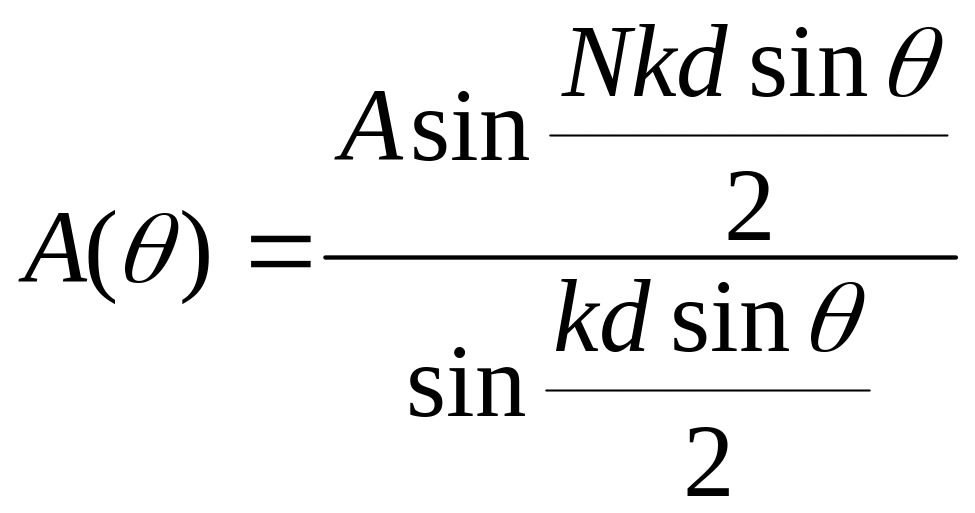в точке
Воспользуемся правилом Лопиталя.
Тогда
При рассмотрение открытой части волнового фронта мы предположим, что источников там очень много
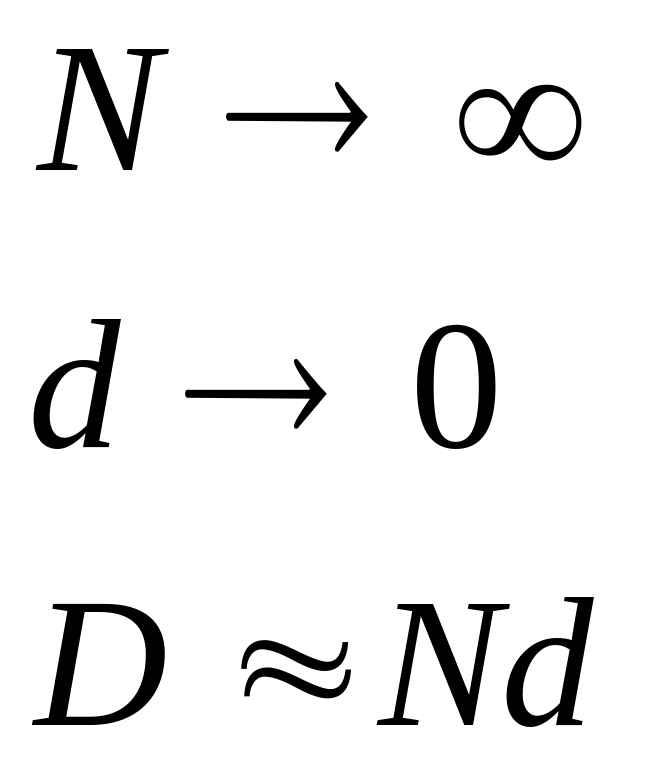
И тогда
и sin в знаменателе можно
разложить в ряд
Тогда получаем :
Заметим, что амплитуда будет равна 0 если
То есть
-
условие минимума
Если
то мы получим условие максимума
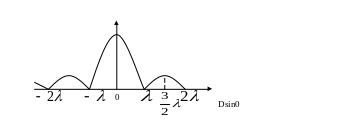
Следует заметить, что амплитуды побочных максимумов будут значительно меньше амплитуды центрального.
После экрана с отверстием мы будем наблюдать волну в виде расходящегося пучка.
Полученный пучок излучения принято характеризовать угловой шириной или расхождением пучка за величину которая выберают половина углового расстояния между ближайшими к нулю нулями амплитуд.
Следует заметить, что размер изображений
отверстий на экране будет
и
будет значительно превышать геометрическое
значение изображения отверстия .
L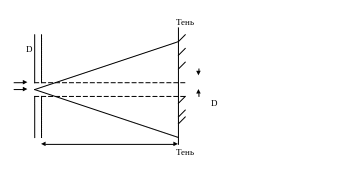
Проникновения изображения в область геометрической тени называется дифракцией.