§1.6 Сложение гармонических колебаний двух частот.
В системе с одной степенью свободы могут существовать колебания только с одной частотой.
Для того чтобы в системе могли наблюдаться колебания с разными частотами должно быть много степеней свободы. Если у нас осциллятор с 2-я степенями свободы, то в нём могут наблюдаться колебания с 2я частотами .
Рассмотрим 2 пружинных маятника
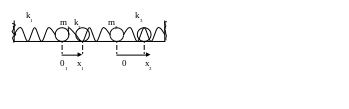
Пусть в положение равновесия все пружины не деформированы, координаты каждого из грузиков будет определяться по отношению к его положению равновесию.
Уравнение 1ого грузика будет
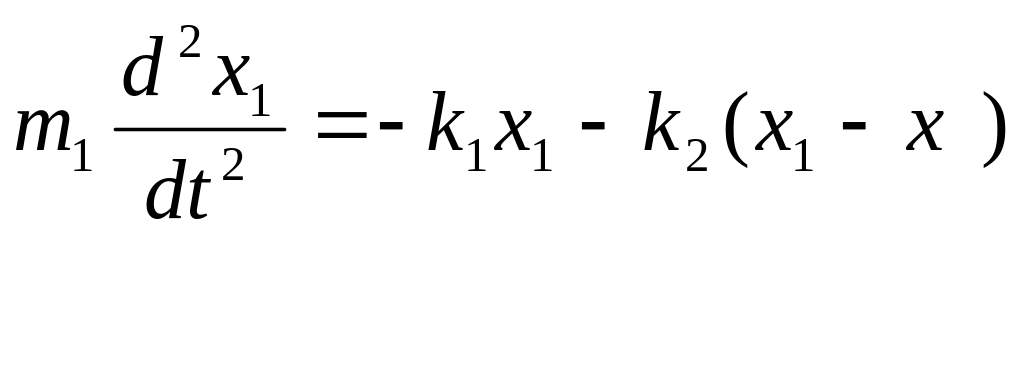
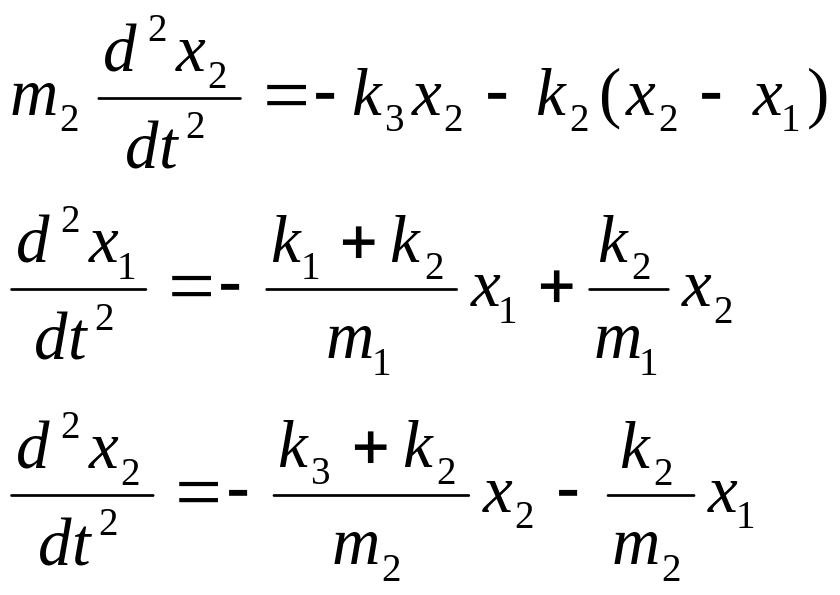
Эту систему уравнений можно переписать в общем виде:
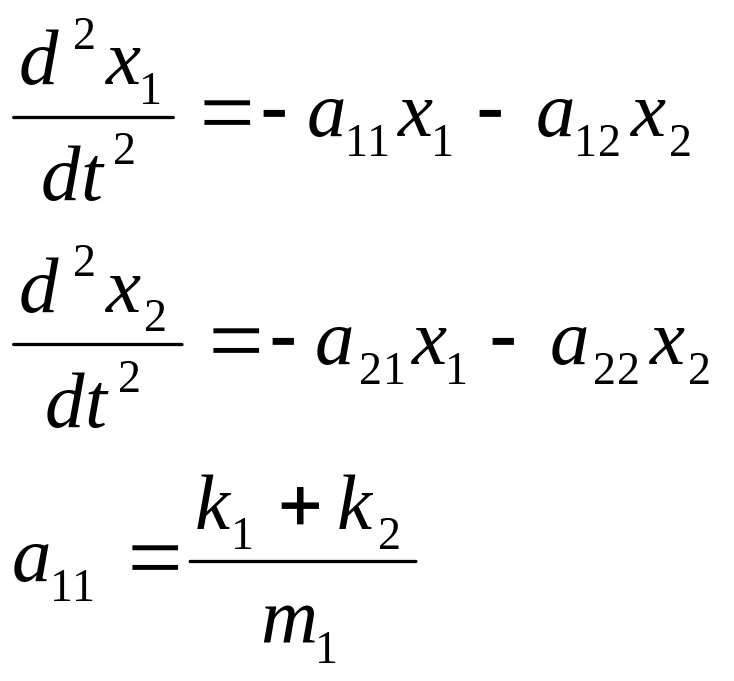
Решение этой системы будем искать в виде :
Подставим в уравнение:
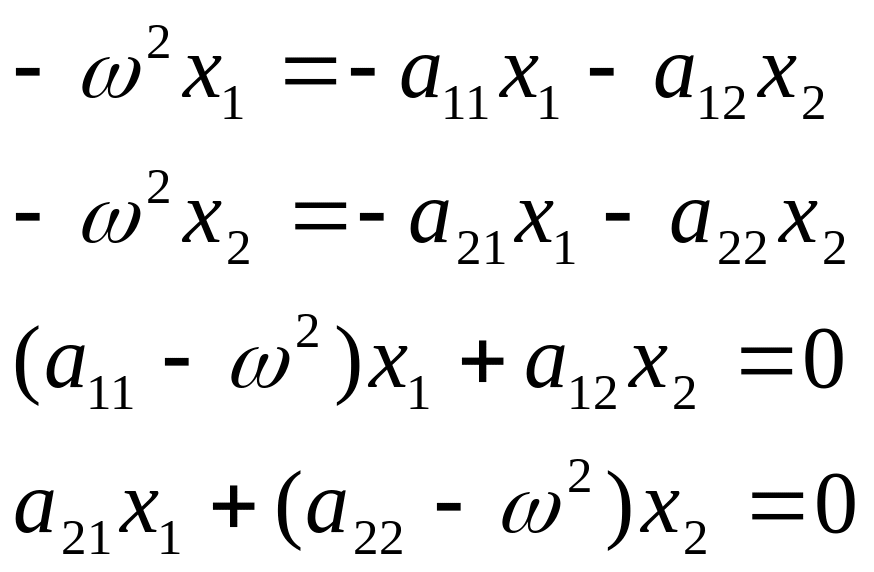
Как известно система линейных, однородных
уравнений имеет нетривиальное
решение
если её определитель равен 0.
Это условие приводит к биквадратному
уравнению для
из
4х корней которых выбираем два
положительных
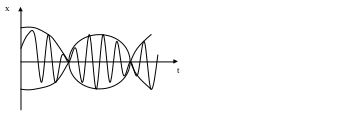
В результате сложения 2х колебаний мы получаем биение. Из математики известно, что система однородных уравнений:
Заменой переменной
,
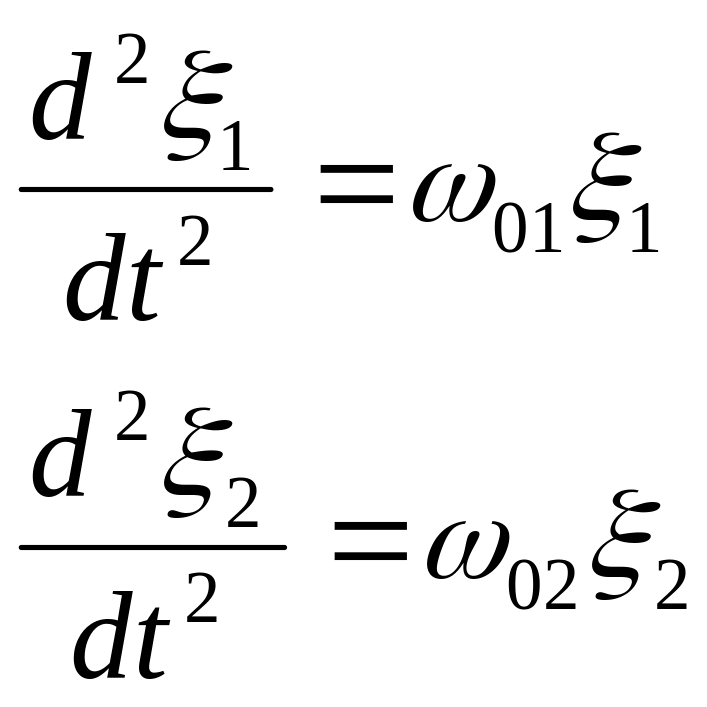
То есть система двух однородных уравнений
распалось на 2 независимых
-
нормальные координаты системы. Такие
координаты существуют всегда .
В нормальных координатах решение:
Каждая нормальная координата будет изменяться по гармоническому закону с одной своей собственной частотой никаких сложений колебаний не происходит. Таким образом сложение гармонических колебаний будет происходить в системе с несколькими степенями свободы при условии, что эта система описывает ненормальными координатам.
§ 1.7 Физические основы анализа Фурье.
Рассмотрим систему которая обладает N степенями свободы, тогда одна из ненормальных координат этой системы будет представлять собой сумму гармонических колебаний различных частот.
Для простоты выберем начало отсчёта таким образом, что на начальные фазы всех складываемых колебаний =0, тогда результирующие колебание будет:
Рассмотрим простейший случай когда интервалы между соседними частотами одинаковы:
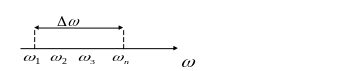
Вычислим эту сумму:
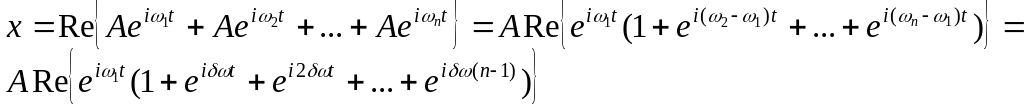
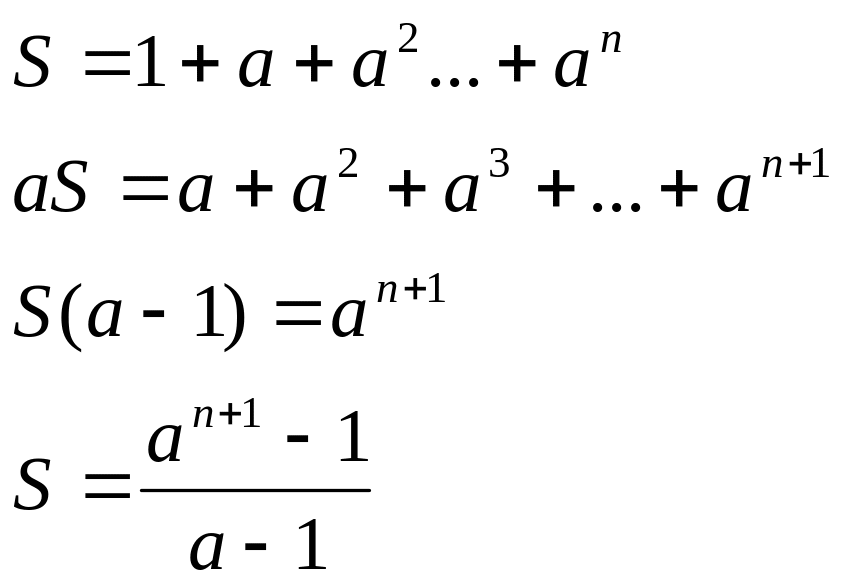
Где
-
средняя частота.
Таким образом при
сложение большого числа колебаний с
различными частотами мы получим колебания
с некоторой средней частотой
амплитуда которого:
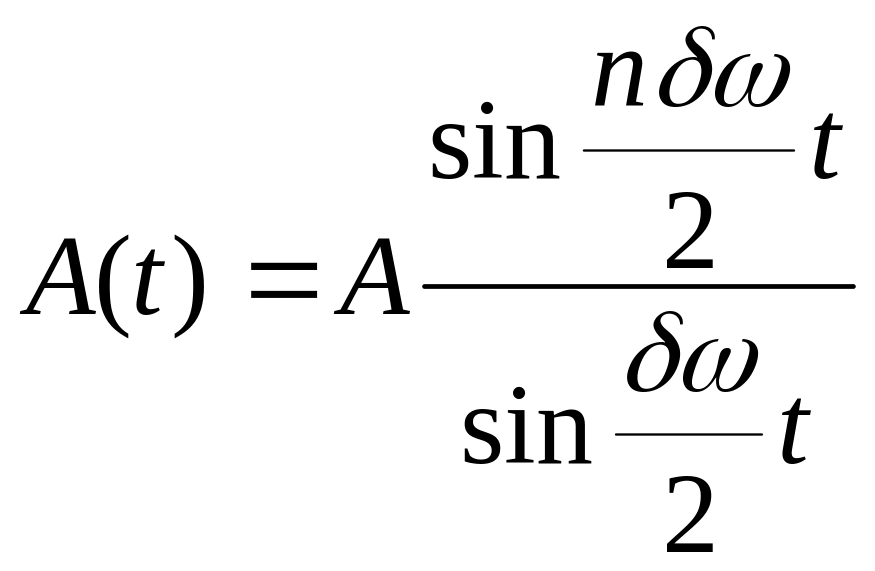
А зависит от t. В этой зависимости есть особая точка t = 0
Для вычисления амплитуды в этой точке воспользуемся правилом Лопиталя.
тогда амплитуда будет
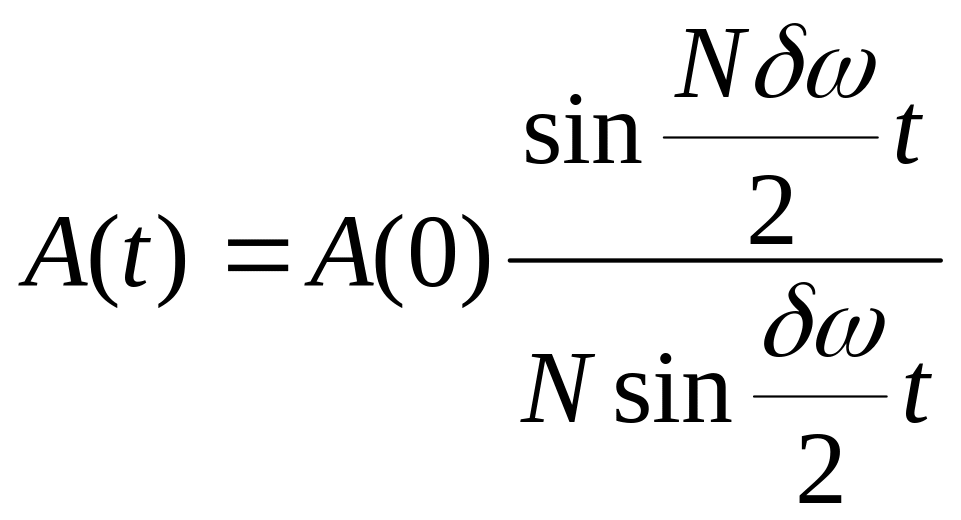
Рассмотрим случай
когда
А при малых углах
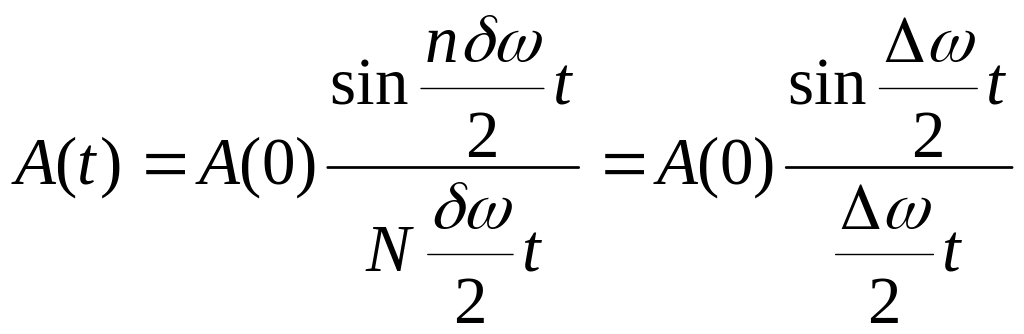
t1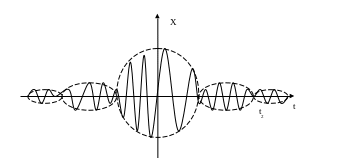
В результате сложения большого числа гармонических колебаний мы получим ограничение во времени колебаний которое называется импульсом.
За длительность импульса
выбирают половину временного интервала
между ближайшими максимальными нулями
амплитуд.
Следует заметить что справедливо и обратное утверждение. Любой произвольный импульс колебаний можно представить в виде суммы гармонических колебаний, такое представление называться анализом Фурье, то есть:
Зависимость амплитуды складываемых колебаний называется спектрам колебаний. В нашем случае спектр колебаний был простой:
A
A
Интервал частот при которых
называется шириной спектра колебаний.
В рассмотренном примере мы получили
соотношение между длиной импульса и
шириной спектра колебаний
Так как был выбран простейший частный
случай, то мы получили и частное
соотношение.
В общем виде
чем короче импульс тем шире спектр.
Пример затухающих колебаний
