
- •По теме: Колебания и волны. Квантовая механика.
- •Содержание:
- •Колебания и волны
- •§1.1 «Свободные гармонические колебания. Уравнение и начальные условия.»
- •§1.2 Затухающие колебания.
- •§ 1.3 Энергия свободных колебаний
- •§1.4 Вынужденные колебания
- •§ 1.5 Вынужденные колебания. Переходный процесс
- •§1.6 Сложение гармонических колебаний двух частот.
- •§ 1.7 Физические основы анализа Фурье.
- •Глава 2. Волны
- •§2.1 Волновой процесс. Волновая функция.
- •§2.2 Гармонические волны.
- •§2.3 Распространение волны в ограниченной среде. Стоячие волны
- •§2.4 Интерференция волн двух источников .
- •§ 2.5 Многолучевая интерференция.
- •§2.6 Дифракция, принцип Гюйгенса
- •§2.7 Дифракционная решётка.
- •§2.8 Принцип Гюйгенса – Фринеля.
- •§2.9 Волновой пакет.
- •§ 2.10 Групповая скорость. Метод стационарных фаз
- •§ 2.11 Пространственная и временная когерентность. Поляризация.
- •§2.12 Приближение геометрической оптики. Уравнение Эйконала.
- •§2.13 Электромагнитные волны в вакууме.
- •§ 2.14 Энергия электромагнитного поля. Вектор Умова-Пойтинга
- •Часть 4 Квантовая механика.
- •§1 Экспериментальные основы квантовой механики.
- •§2 Волны де Бройля
- •§ 3 Уравнение Шредингера.
- •§4 Принцип неопределенности Гейзенберга
- •§ 5 Движение частицы в поле с потенциальным барьером. Туннельный эффект.
- •§6 Частица в потенциальной яме. Дискретность энергетического состояния.
- •§7 Атом водорода.
- •§8 Принцип Паули. Периодическая таблица элементов.
- •§9 Электрон в периодическом поле. Энергетические зоны.
§1.4 Вынужденные колебания
Анализ решения. Резонансные характеристики.
Рассмотрим систему на которую действует
внешняя сила
![]() .
Если это пружина маятника, то уравнение
будет иметь вид:
.
Если это пружина маятника, то уравнение
будет иметь вид:
![]()
![]()
Рассмотрим самый важный случай когда внешняя сила периодична.
![]()
![]()
Для того чтобы найти решение этого уравнения рассмотрим комплексное уравнение реальная часть которого совпадает с нашим уравнением.
![]()
Решение уравнения будем искать в виде:
![]()
![]()
![]()

![]()
![]()
![]()
![]()


![]() ,
где
,
где

Таким образом найденное решение уравнения
вынужденных колебаний представляет
собой гармонические колебания амплитуда
которых полностью определяется
параметрами осциллятора и частотой
![]() -вынуждающая сила
-вынуждающая сила
Тоже самое касается и начальной фазы
колебаний
![]() .
Другими словами полученное решение
независит от начальных условий, а поэтому
не является общим и единственным. Это
частное решение уравнения вынужденных
колебаний.
.
Другими словами полученное решение
независит от начальных условий, а поэтому
не является общим и единственным. Это
частное решение уравнения вынужденных
колебаний.
![]()

![]()
Амплитуда колебаний зависит от параметров
системы
![]() и
частотой
-
вынуждающей силы. Зависимость амплитуды
от
называется амплитудно-частотный
характеристикой системы.
и
частотой
-
вынуждающей силы. Зависимость амплитуды
от
называется амплитудно-частотный
характеристикой системы.

Такая зависимость называется резонансной, а частота R (при которой амплитуда максимальна) называется резонансной частотой. Если = R то говорят, что в системе наблюдается резонанс амплитуд.
Для нахождения резонансной частоты
нужно приравнять к 0, производную
![]()
Легко заметить, что достаточно приравнять к нулю производную от подкоренного выражения
![]()
![]()
![]()
![]()
Зависимость базового сдвига от частоты называется фазово-частотной характеристикой.

Рассмотрим скорость вынужденных
колебаний
![]()
 -
амплитуда скорости.
-
амплитуда скорости.

Полученная зависимость называется
резонансом скорости. Для определения
частоты при которой V0
= max надо
![]() .
.
Полученное решение уравнения вынужденных колебаний представляет собой гармоническое колебание. В §1.3 было показано, что энергия гармонических колебаний постоянна. В §2.4 из 1ой части курса было сказано, что полная энергия системы сохраняется, если сумма мощностей всех не потенциальных сил = 0.
В нашей системе таких сил 2: сила трения
и внешняя сила. Как известно мощность
силы будет :
![]()
![]()
Пусть N- мощность внешних сил
![]()
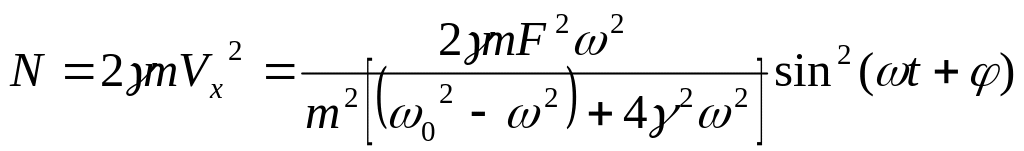
![]() -мощность
внешних сил
-мощность
внешних сил
Очевидно, что среднее значение мощности вынуждающей силы будет:


Так как средняя мощность пропорциональна
квадрату амплитуды скорости, то резонанс
мощности будет происходить при той же
частоте, что и резонанс скорости, то
есть при
0
, осциллятором в котором
происходит вынужденные колебания
принято характеризовать полимерной
![]() резонансной
кривой, которая определяется на уровне
половины максимальной средней мощности.
резонансной
кривой, которая определяется на уровне
половины максимальной средней мощности.
Рассмотрим систему со слабым затуханием
когда
![]() ,
так как при уменьшение затухания ширина
резонансной кривой уменьшается, тогда
:
,
так как при уменьшение затухания ширина
резонансной кривой уменьшается, тогда
:
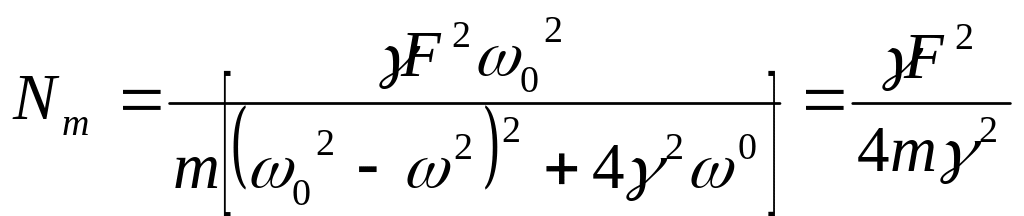

![]()
![]()
§ 1.5 Вынужденные колебания. Переходный процесс
Решение полученное в § 1.4 уравнение вынужденных колебаний не зависит от начальных условий и поэтому не является единственным и общим. Это частное решение
![]()
Для общего решения заметим, что сумма решений нашего уравнения и уравнений затухающих колебаний:
![]()
Будет являться решением уравнения вынужденных колебаний, для этого чтобы в этом убедиться:
![]()
![]() то есть x1+x2
является решением
уравнения вынужденных колебаний мы
учли, что уравнение затухающих колебаний
имеет вид:
то есть x1+x2
является решением
уравнения вынужденных колебаний мы
учли, что уравнение затухающих колебаний
имеет вид:
![]()
![]() -
определяются параметрами системы
-
определяются параметрами системы
![]() -
являются произвольными и определяться
из начальных условий. Поэтому полученное
решение является общим и единственным
при заданных начальных условиях.
-
являются произвольными и определяться
из начальных условий. Поэтому полученное
решение является общим и единственным
при заданных начальных условиях.
![]()
Рассмотрим частный случай нулевых начальных условий.

Подставим начальные условия в решение
![]()
Будем считать точно также как в §1.3, что затухание слабое. Тогда:
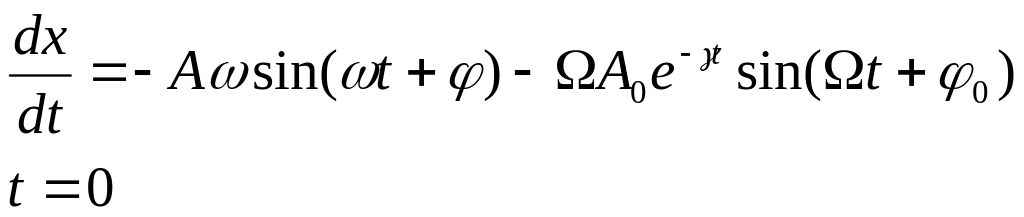
![]()
![]()
![]()
![]()

Таким образом мы нашли две произвольные величины, которые удовлетворяют нулевым начальным условиям.
Рассмотрим случай, когда
![]()

Так как х(0)=0 , то знак «+» не подходит
![]()

Таким образом полученное ранение состоит из двух частей, при этом вторая часть с течением времени уменьшается и через время релаксации практически исчезает и начиная с этого времени в системе будут наблюдаться колебания формулы которых были получены в §1.4.
При это говорят в системе наблюдается установившейся или стационарный процесс. Поэтому частное решение из §1.4 часто называется стационарным решением.
Это решение от начальных условий не
зависит если
![]()
То существуют обе части решения и в
системе наблюдается переходный процесс.
Форма этого процесса определяется
начальными условиями. Рассмотрим случай,
когда в системе нет затухания, при
нулевых начальных условиях
![]() тогда)
тогда)
![]()
![]()
![]()
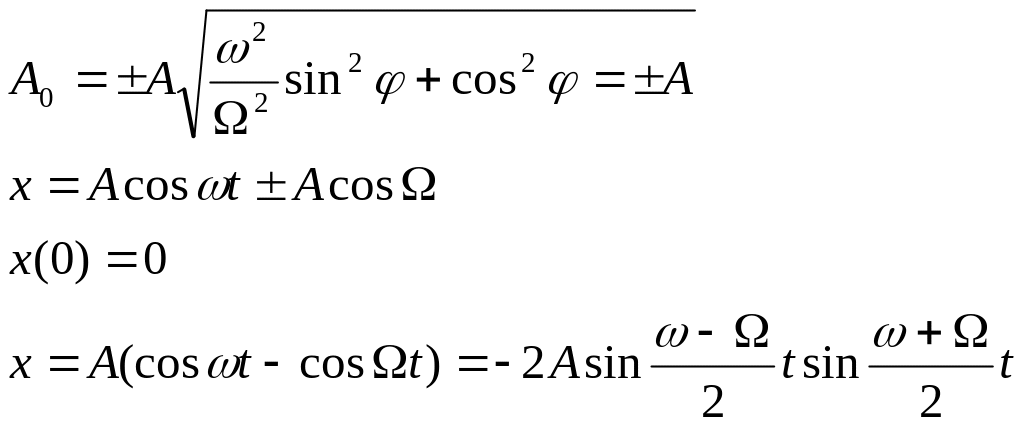
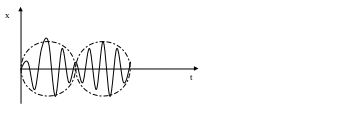
Таким образом при
![]() в системе никогда не будет наблюдаться
установившееся решение. Всё время
переходит процесс. Колебание такого
вида- биение.
в системе никогда не будет наблюдаться
установившееся решение. Всё время
переходит процесс. Колебание такого
вида- биение.
