§4 Принцип неопределенности Гейзенберга
Рассмотрим одномерный случай, когда
Если волновая функция частицы представляют собой волновой пакет протяжённостью
Таким образом очевидно вероятность обнаружения частиц будет отличаться от 0 только там где существует волновой пакет.
Таким образом о местоположение частицы можно говорить лишь с некоторой не определённостью Для определения которой выполним § 2.9
Где
не
определённость координатами частицы,
а
не
определённость её импульсом.
Соотношение неопределенности Гейзенберга для координат и импульса.
Если мы точно знаем координаты частицы
,
то мы не знаем, как она двигается
.
Если мы находимся в некоторой точке, и мимо нас пролетает частица, то есть мимо нас распространяется волновой пакет, то мы будем наблюдать импульс колебаний.
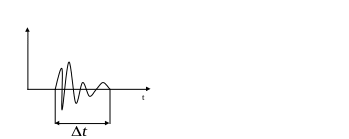
длительность импульса определяет неопределенность времени, когда частица находится в данной точке пространства, то есть частица находилась в данной точке пространства в течение с разной вероятностью. В §1.7 было показано
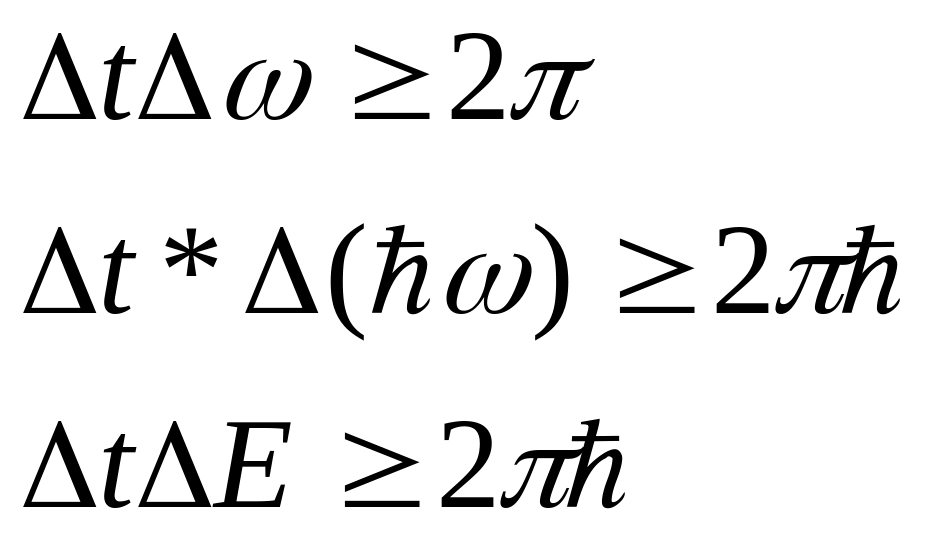
То есть если мы точно знаем время, то не знаем энергию.
§ 5 Движение частицы в поле с потенциальным барьером. Туннельный эффект.
Рассмотрим одномерный случай, когда положение частицы х. Пусть потенциальная энергия частицы имеет форму барьера.
Так как сила действующая на частицу
Рассмотри частицу, полная энергия
которой
Для определения волновой функции при
заданной энергии
достаточно рассмотреть стационарное
уравнение Шредингера, из которого
находим
В одномерном случае
1) Рассмотрим
Как известно решение этого уравнения будет иметь вид
общие решение
Таким образом в полученном решение у нас будет 2-е волновые функции: вдоль Х («падающая волна») и волна против Х (отражённая волны)
-
определят плотность вероятности
обнаружить частицу, которая двигается
к потенциальному барьеру.
плотность вероятности обнаружения
отражённую частицу.
-коэффициент
отражения.
2) Рассмотри x>0
Решение уравнения имеет вид
Тогда
Заметим, что решение eqx при x > 0 не подходит, так как оно не удовлетворяет условиям нормировки, поэтому
Таким образом в области x>0 существует отличная от 0 волновая функция частиц и сумм вероятности обнаружить частицу за потенциальным барьером. Для того чтобы найти коэффициент отражения, запишем условие непрерывности волновой функции и её производной в точке х = 0
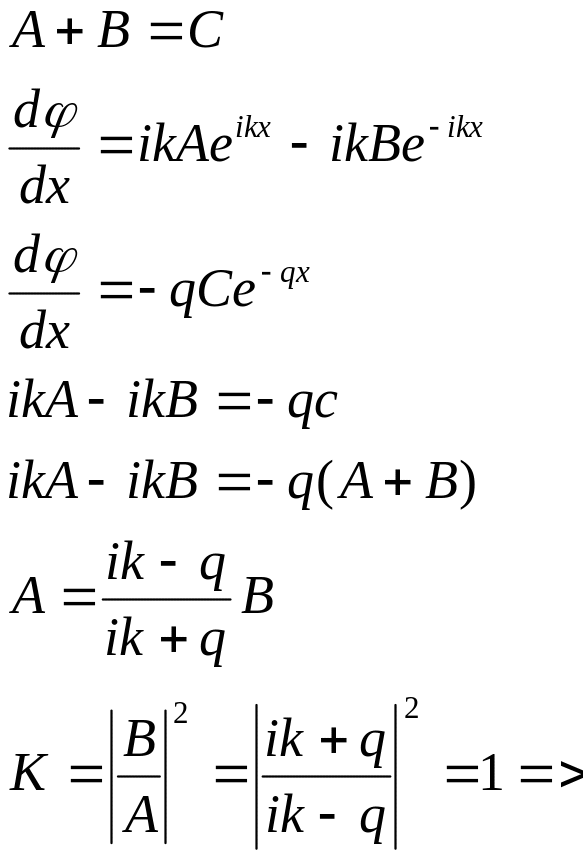
В области x<0 вероятность
обнаружения падающую и отражённую
одинакова. Так как решение найдено при
по
Туннельный эффект.
Рассмотри движение частицы в поле с потенциальным барьером вида
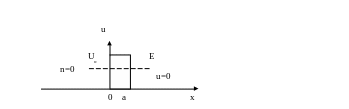
Предположим, что частица находилась сначала в области x<0 , , тогда в области x<0 решением стационарного уравнения Шредингера будет иметь вид
Таким образом существует вероятность,
что частица может пройти потенциальный
барьер и область x<0 в
области x>a. Эта вероятность
характеризуется коэффициентом
пропускания, который равен квадрату
модуля отношения
Таким образом если потенциальный барьер
бесконечно широкой, то
и
если он бесконечно высок
