Конспект лекций по физике
за 2 семестр
По теме: Колебания и волны. Квантовая механика.
Преподаватель: Постников С. А.
Конспект подготовила: Багаутдинова Д. Ж.
группа СС0606
Москва 2007г.
Содержание:
Часть3. Колебания и волны
Глава 1. Колебания и волны
§ 1.1. Свободные гармонические колебания. Уравнение и начальные условия ………..1
§1.2.Затухающие колебания ………………………………………………………………..4
§ 1.3. Энергия свободных колебаний…………...……………………………………….....6
§ 1.4. Вынужденные колебания. Анализ решения. Резонансные характеристики...……7
§ 1.5. Вынужденные колебания. Переходный процесс...…………………………………11
§ 1.6. Сложение гармонических колебаний двух частот………………………………….14
§ 1.7. Физические основы анализа Фурье………………………………………………….16
Глава 2. Волны
§2.1. Волновой процесс. Волновая функция……………………………………………….18
§ 2.2 Гармонические волны…………………………………………………………………21
§2.3. Распространение волны в ограниченной среде. Стоячие волны…………………...22
§2.4. Интерференция волн двух источников……………...………………………………..25
§2.5. Многолучевая интерференция…………………………...……………………………29
§2.6. Дифракция, принцип Гюйгенса……………………………………………………….31
§2.7. Дифракционная решетка……………………………………………………………….34
§2.8. Принцип Гюйгенса – Фринеля. Дифракция Фринеля……………………………….37
§2.9. Волновой пакет…………………………………………………………………………40
§2.10. Групповая скорость. Метод стационарных фаз……………………………………..43
§2.11. Пространственная и временная когерентность. Поляризация……………………..45
§2.12. Приближение геометрической оптики. Уравнение Эйконала. Принцип Ферма…48
§2.13. Электромагнитные волны в вакууме………………………………………………...50
§2.14. Энергия электромагнитного поля. Вектор Умова-Пойнтинга……………………..52
Часть 4. Квантовая механика
§ 1. Экспериментальные основы квантовой механики…………………………………….53
§ 2. Волны де Бройля…………………………………………………………………………56
§ 3. Уравнение Шредингера………………………………………………………………….57
§ 4. Принцип неопределенности Гейзенберга………………………………………………60
§ 5. Движение частицы в поле с потенциальным барьером. Туннельный эффект……….61
§ 6. Частица в потенциальной яме. Дискретность энергетических состояний…………...64
§ 7. Атом водорода……………………………………………………………………………66
§ 8. Принцип Паули. Периодическая таблица элементов………………………………….68
§ 9. Электрон в периодическом поле. Энергетические зоны……………………………....70
Часть 3
Колебания и волны
§1.1 «Свободные гармонические колебания. Уравнение и начальные условия.»
Для описания число независимых переменных необходимо для описания механических систем называется числом степеней свободы.
Рассмотрим систему с одной степенью свободы для описания которой будем использовать одну переменную х. Это могут быть либо координата, либо угол, либо заряд. В целом ряде задач эта переменная удовлетворяет уравнению вида
В качестве примера такой системы возьмём пружинный маятник без трения.
ax-первая
производная проекции скорости
-
изменение длинны
-называется линейным, дифференциальным, однородным 2-го порядка.
Будем искать решение в виде
Подставим функции в уравнение
Полученное решение называется гармоническим колебанием, , называется уравнение гармонических колебаний .
Система которая описывает уравнение называется гармоническим осциллятором.
циклическая
частота
-фаза
колебаний
-начальная
фаза
t- в течение которого фаза
колебаний меняется на
,период
колебания
частота колебаний
Поэтому значение x = 0 называют положением равновесия.
А величину x называют смещением независимо от того что она из себя представляет.
Полученное решение содержит 2 произвольные
постоянные величины
.
Уравнение гармонических колебаний
определяет лишь частоту колебаний в
рассматриваемом примере.
Для определения амплитуды и начальной фазы необходимо дополнительные условия, в качестве таких условий обычно используют начальные условия задачи , то есть значение смещения.
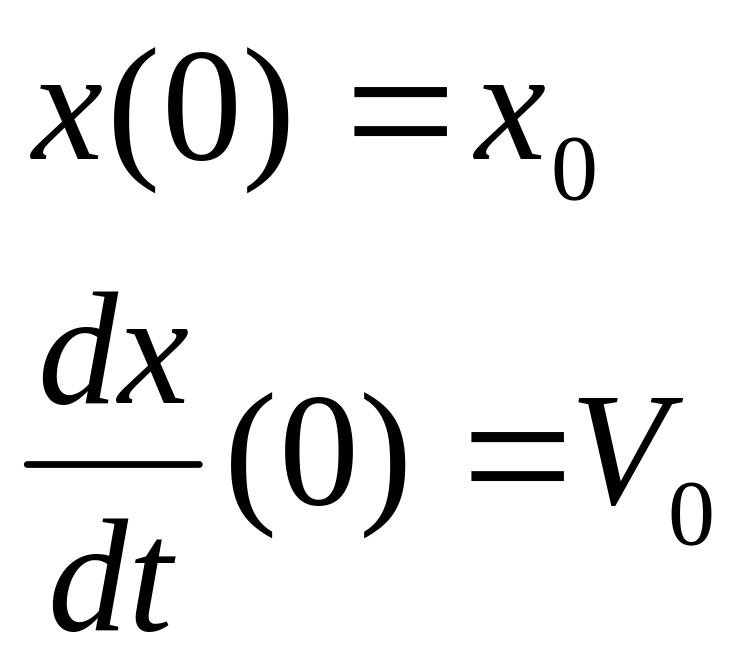
2
+
2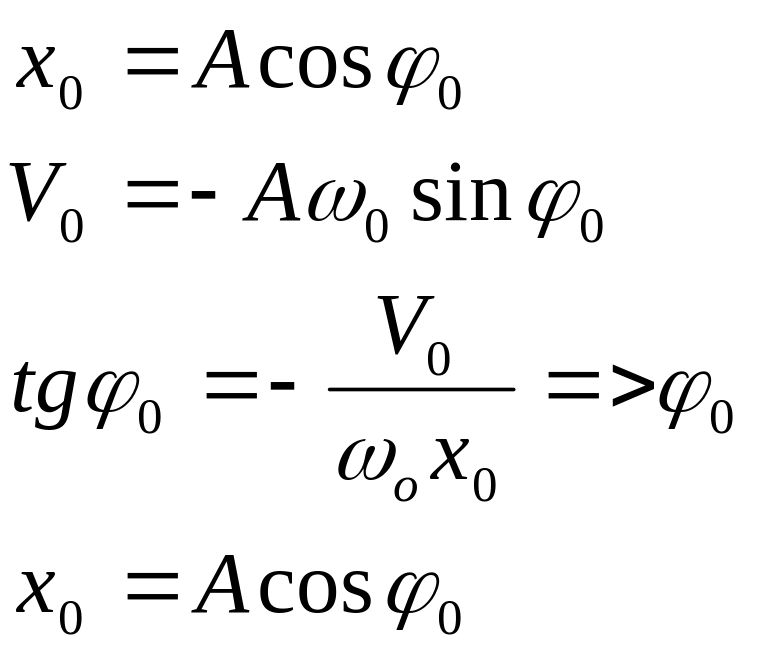
-
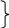
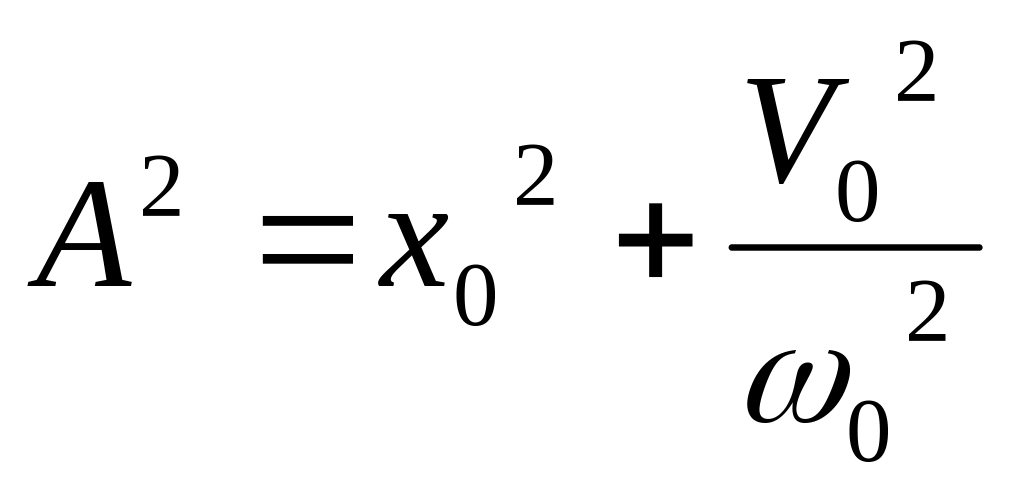
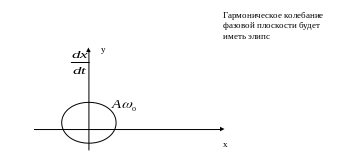
фазовая плоскость
