4. Правило составления уравнения прямой

Положение прямой на плоскости относительно системы координат можно задать различными способами. Прямая может быть задан точкой и направлением; точкой и перпендикулярным прямой вектором; двумя точками; отрезками, которые прямая отсекает на осях координат (частный случай задания прямой двумя точками).

Мы видим, что во всех случаях задания прямой обязательной должна быть известна хотя бы одна точка, через которую проходит искомая прямая. Кроме того, должно быть задано какое-либо дополнительное условие: коллинеарность, перпендикулярность или вторая точка, принадлежащая прямой.

Правило составления уравнения прямой l, для которой известны координаты точки М₁ (х₁; у₁) и задано какое-либо второе условие, состоит в следующем:

1. На прямой l выбирают произвольную точку с текущими координатами х, у: М (х; у).

2. Находят координаты вектора, лежащего на прямой l и такого, что его начало есть точка М₁ (х₁; у₁), а конец - точка М (х; у),

3. Записывают координаты вектора, заданного дополнительными условиями (коллинеарности, перпендикулярности, двумя точками), т.е. направляющего или нормального вектора .

4. Используют условие коллинеарности или перпендикулярности векторов и .

5. Уравнение прямой, проходящей через данную точку и имеющей заданный нормальный вектор

Нормальным вектором прямой l называется любой ненулевой вектор , перпендикулярный этой прямой.

Пусть заданы точка М₁ (х₁; у₁) и нормальный вектор . Для составления уравнения прямой, проходящей через точку М₁ и имеющей нормальный вектор , воспользуемся общим правилом:

1. Выберем на прямой l произвольную точку М (х; у).

2. Найдем координаты вектора :

3. Запишем координаты заданного нормального вектора : .

4. Воспользуемся условием перпендикулярности векторов: их скалярное произведение равно нулю, т.е. 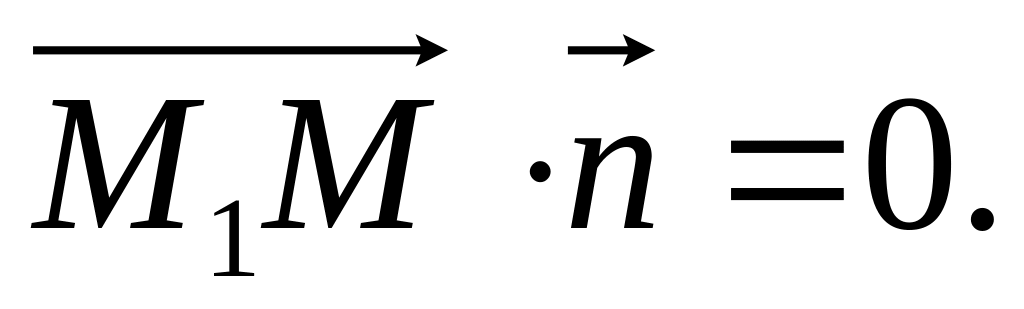Так как скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат, то уравнение прямой l примет вид

А(х – х₁) + В(у – у₁) = 0.

Заметим, что если известно общее уравнение прямой, то координаты нормального вектора равны коэффициентам при х и у в этом уравнении.

Пример 2. Известны точка М1 (7; -8) и нормальный вектор прямой = (2; 3). Составить уравнение прямой. Р е ш е н и е: 1) Выбираем точку М (х; у). 2) Найдем вектор = (х – 7; у +8). 3) Нормальный вектор = (2; 3), т.е. А = 2, В = 3. 4) Запишем уравнение искомой прямой 2(х – 7) + 3(у +8) = 0, откуда 2х – 14 + 3у +24 = 0; 2х + 3у + 10 = 0 – искомое уравнение в общем виде.

6. Уравнение прямой, проходящей через данную точку и имеющей заданный направляющий вектор

Направляющим вектором прямой l называется ненулевой вектор = (a; b), параллельный этой прямой. Любая прямая имеет бесконечное множество направляющих векторов, коллинеарных между собой.

Пусть заданы точка М₁ (х₁; у₁), через которую проходит прямая l , и ее направляющий вектор = (a; b).

Используя общее правило, составим уравнение прямой l .

1. Выберем на прямой l произвольную точку М (х; у).

2. Найдем вектор

3. Запишем направляющий вектор = (a; b).

4. Воспользуемся условием коллинеарности векторов и , их одноименные координаты должны быть пропорциональны. Поэтому уравнение прямой l имеет вид .

Пример 3. Составить уравнение прямой, проходящей через точку А (3; -2) и имеющей направляющий вектор = (-5; 3). Р е ш е н и е: 1) Выберем на искомой прямой произвольную точку М (х; у). 2) Найдем вектор 3) Направляющий вектор = (-5; 3). 4) Запишем уравнение прямой , откуда 3х – 9 = -5у – 10; 3х + 5у + 1 = 0 – искомое уравнение в общем виде.